10. Механіка твердого тіла.

1. Ступені свободи та зв’язки.

Положення точки в просторі можна задати з допомогою трьох незалежних координат (x, y, z ; ρ, φ, z ; r, φ, θ і т.д.). Про точку, яка переміщується в просторі як завгодно, говорять, що вона має три ступені свободи.

Матеріальна точка математичного маятника може переміщуватися лише по поверхні сфери з центром в точці закріплення. В тих випадках, коли матеріальна точка змушена знаходитись на якій-небудь заданій поверхні, говорять, що на рух матеріальної точки накладено зв’язки. Оскільки в рівнянні поверхні ƒ(x,y,z) = 0 тільки дві координати є незалежними, то така точка має два ступеня свободи.

Точка, що може переміщуватися лише вздовж заданої кривої, має один ступінь свободи, оскільки для визначення її положення достатньо однієї незалежної координати.

Число незалежних координат (або параметрів), якими визначається рух матеріальної точки (чи системи матеріальних точок) називають числом її ступенів свободи.

Число ступенів свободи двох незалежних матеріальних точок дорівнює шести. Якщо ж ці точки зв’язані стержнем незмінної довжини l, то шість координат вже не будуть незалежними, оскільки між ними існує співвідношення :

,

(10.1)

з якого одну з шести координат можна виразити через довжину l та інші п’ять координат. Отже така система має п’ять ступенів свободи. Число ступенів свободи позначають буквою і:

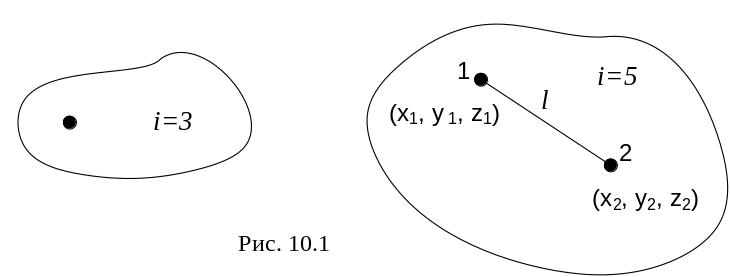
Система, що складається з N матеріальних точок, описується 3N координатами. Якщо точки системи незалежні, то така система має 3N ступенів свободи.

Абсолютно твердим тілом називають ідеалізовану систему матеріальних точок, відстані між якими під час руху системи не змінюються з часом.

Абсолютно тверде тіло, якщо на його рух не накладено ніяких обмежень, має шість ступенів свободи.

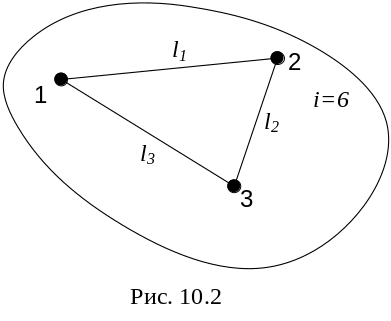
Положення твердого тіла однозначно визначається положенням трьох точок, що не лежать на одній прямій (рис.10.2). Положення цих трьох точок описуються дев’ятьма параметрами, між якими є зв’язок що задається трьома рівняннями типу (10.1). Отже число незалежних параметрів дорівнює шести.

2. Рівняння руху та умови рівноваги твердого тіла.

Оскільки тверде тіло є механічною системою, число ступенів свободи якої дорівнює 6, то для описання його руху потрібно шість незалежних числових рівнянь. Замість них можна взяти два незалежних векторних рівняння. Цими рівняннями є:

рівняння руху центра мас: (10.2)

та рівняння моментів: (10.3)

Рівняння (10.2) і (10.3) називають рівняннями руху твердого тіла. В них входять лише зовнішні сили, оскільки внутрішні сили можуть змінювати лише взаємне розташування і швидкості матеріального тіла, а для абсолютно твердого тіла такі зміни неможливі. Для абсолютно твердого тіла точки прикладання зовнішніх сил можна переносити вздовж лінії дії сили, при цьому і не змінюються.

Якщо тверде тіло нерухоме, то (10.2) і (10.3) переходять в;

, .

(10.4)

Вирази (10.4) є необхідними умовами рівноваги твердого тіла. Вони не достатні, бо при виконанні цих умов центр мас може рухатись прямолінійно і рівномірно з довільною швидкістю, а саме тіло може обертатись, зберігаючи обертовий імпульс.

Оскільки в рівновазі , то момент цих сил в стані рівноваги дорівнює нулю відносно будь-якого нерухомого полюса О. Тому під час розв’язування будь-якої задачі на рівновагу твердого тіла початок О можна вибирати довільно, що можна використати для спрощення самого розв’язку.

Самостійно пропонується розглянути такі питання:

1. Знаходження точки прикладання сили реакції опори, що діє на брусок, який лежить на похилій площині.

2. Додавання паралельних сил.

3. Види рівноваги.