12. Гідродинаміка ідеальної та реальної рідини.

1. Стаціонарний рух ідеальної рідини. Рівняння нерозривності струменя.

Під час кінематичного описання руху рідини можна вказувати траєкторії руху кожної частинки рідини і швидкості частинок в кожній точці траєкторії. Але можна вказати швидкості всіх частинок рідини в деякий момент часу . Одержану миттєву картину розподілу швидкостей називають полем швидкостей (рис. 12.1).

Лінія, дотична до якої співпадає з швидкістю частинки рідини, що міститься в даний момент часу в точці дотику, називається лінією течії (рис. 12.2).

Якщо лінії течії (отже, і поле швидкостей, якому відповідають ці лінії) з часом не змінюються, то рух рідини назиають стаціонарним.

Під час стаціонарної течії рідини лінії течії співпадають з траєкторіями частинок рідини.

Течія називається ламінарною, якщо вздовж потоку кожний виділений тонкий шар ковзає відносно сусідніх, не змішуючись з ними, і турбулентною (вихровою), якщо вздовж потоку відбувається інтенсивне перемішування рідини (газу). Далі розглядатимемо ламінарну течію.

Візьмемо довільний замкнутий контур С і через кожну його точку проведемо лінії течії. Ці лінії розташуються по деякій трубчатій поверхні, що називається трубкою течії (рис. 12.3). Оскільки швидкість частинок рідини направлена по дотичній до ліній течії, то під час руху частинки рідини не перетинають трубку течії. Якщо поперечний переріз трубки течії досить малий, то можна вважати швидкість рідини в різних точках перерізу однаковою. Тоді маса рідини, що протікає через поперечний переріз площею за час  , дорівнює:

,

(12.1)

де - густина рідини. У випадку стаціонарної течії буде одним і тим же для будь-якого перерізу трубки течії. Для двох перерізів з площами і :

(12.2)

Формула (12.2) означає сталість маси рідини між перерізами і та стаціонарність течії. Якщо , тобто рідина не стискується і струмінь не має розривів, то:

, або

(12.3)

Формулу (12.3) називають рівнянням нерозривності струменя.

2. Рівняння бернуллі для ідеальної рідини. Формула торрічеллі.

Розглянемо стаціонарну течію ідеальної рідини в консервативному силовому полі, наприклад, полі сили тяжіння. Виділимо в рідині вузьку трубку течії між перерізами і . За час через переріз увійде об’єм рідини, рівний ; через переріз вийде об’єм рідини, рівний (рис. 12.4).

Якщо течія стаціонарна, то в об’ємі трубки течії між перерізами і ніяких змін не відбудеться. Тому досить розглянути лише зміни, що відбудуться з елементами та . Можна вважати, що елемент немов би перемістився в положення . В ідеальній

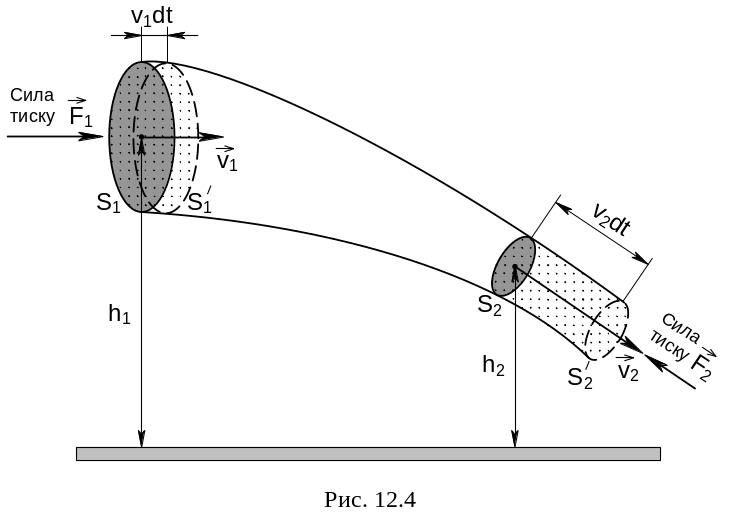
Рідині сили тертя не діють, тому на елементи рідини діють лише сили тяжіння та тиску. За теоремою про кінетичну енергію робота цих сил дорівнює приросту кінетичної енергії виділеного об’єму рідини.

; ; .

В лівій частині рівняння враховано, що робота сили тяжіння дорівнює зміні потенціальної енергії, взятої з протилежним знаком .

Враховуючи рівняння нерозривності струменя (12.3), скоротимо на і перенесемо члени з однаковими індексами в одну сторону рівняння:

,

(12.4)

або:

(12.4')

Рівняння (12.4) називають рівнянням Бернуллі.

Розглянемо наслідки з цього рівняння.

• Тиск в трубці змінного перерізу.

Нехай вісь трубки течії розташована горизонтально (рис. 12.5) і ; тоді (12.4) перепишеться так:

,

звідки ; оскільки , то:

(12.5)

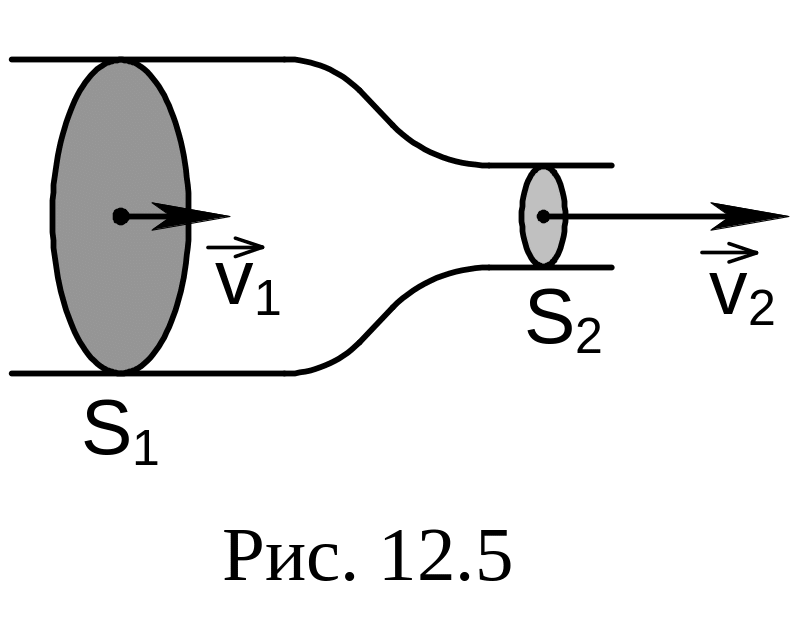
З (12.5) випливає, що : тиск у вузькій частині трубки течії менший, ніж в широкій. Одержаний висновок може бути пояснений на основі другого закону Ньютона. Він має широке технічне застосування: водоструминні насоси, карбюратори, пульверизатори та ін.