2.5 Аттрактори динамічних систем. Типи фазових портретів

Розглянемо динамічну систему, що задається системою лінійних диференціальних рівнянь:

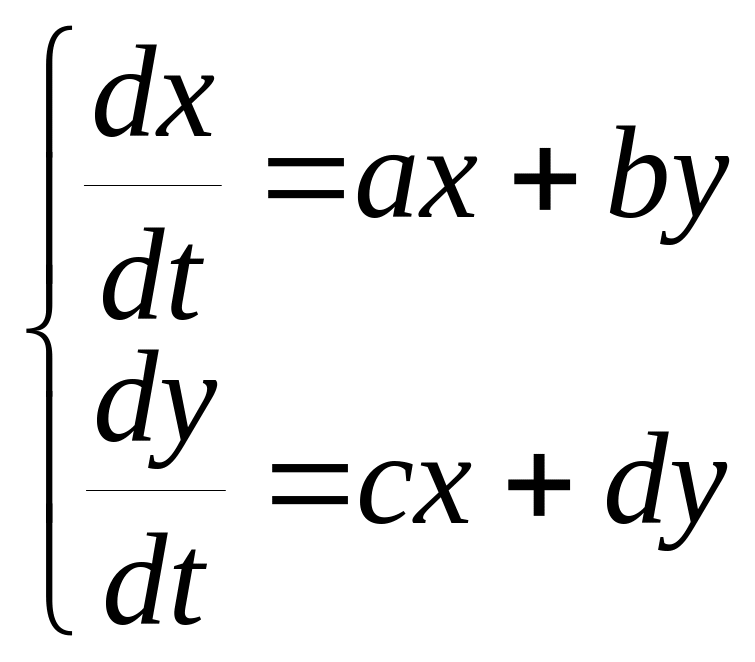матриця параметрів

і хай і – корені характеристичного рівняння матриці параметрів.

1.Якщо і дійсні і обидва менше нуля, то фазовий портрет називається стійкий вузол, всі траєкторії проходять через стаціонарну точку і з часом вони до неї сходяться (рис 6).

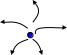
Рисунок 6 – Стійкий вузол Рисунок 7 – Нестійкий вузол

2.Якщо обидва корені дійсні і позитивні, то фазовий портрет називається нестійкий вузол (рис.7).

3.Якщо обидва корені дійсні, але різних знаків, то фазовий портрет називається сідло.

Рисунок 8 – Сідло

На рис.8 особлива точка умовно поміщена на початку координат. Траєкторії, яким належить особлива точка, називаються сепаратрисами.

4.Якщо корені комплексні, а дійсна частина у них позитивна, то фазовий портрет називається нестійкий фокус (рис.9).

5.Якщо корені комплексні з негативними дійсними частинами, то фазовий портрет називається стійкий фокус (рис.10).

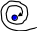
Рисунок 9 – Нестійкий фокус Рисунок 10 – Стійкий фокус

6.Якщо корені комплексні, такі, що мають тільки уявну частину, то фазовий портрет називається граничний цикл (рис.11).

Рисунок 11 – Граничний цикл

У околі особливих точок фазові траєкторії можуть бути шести типів, схемний показаних на рисунках (стрілки на фазовій траєкторії указують напрям зміни параметра t).

Класифікація типів поведінки фазових кривих в околиці особливої точки була здійснена великим французьким математиком і філософом Анрі Пумнкаре (1854—1912), який ввів також поняття граничного циклу, що грає найважливішу роль в різних додатках теорії диференціальних рівнянь.

Граничним циклом диференціального рівняння називається ізольований періодичний розв’язок цього рівняння.

2.6 Приклад розв’язку першого завдання

Завдання

В результаті економічного аналізу встановлено, що поведінка системи залежить від двох змінних x і у і описується системою лінійних диференціальних рівнянь:

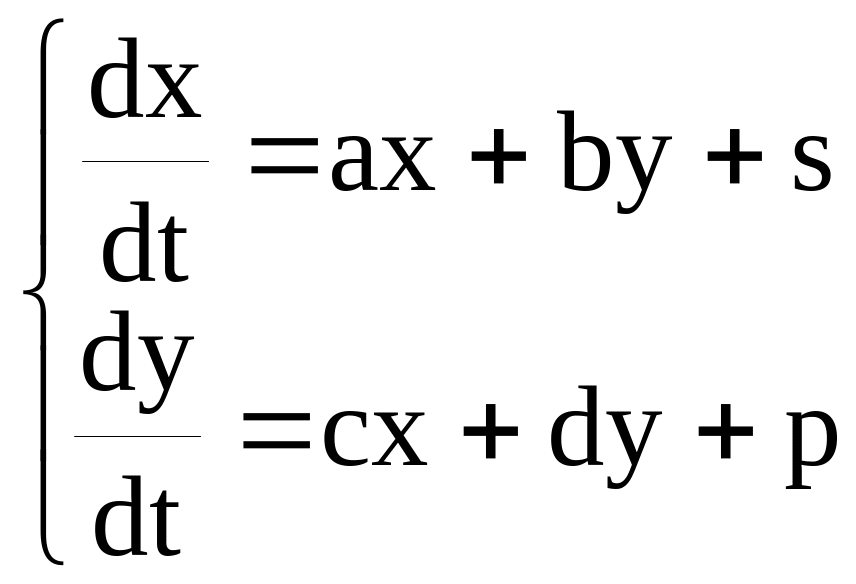
При заданих значеннях параметрів визначити:

• тип динамічної системи

• координати точки рівноваги системи у фазовому просторі

• тип поведінки системи: стійкість, наявність аттрактора

• побудувати фазовий портрет системи

1) .

Розв’язок

1.Динамічна система автономна (час в явному вигляді не присутній), лінійна, безперервна, задається системою диференціальних рівнянь.

2. Стаціонарна точка (точка рівноваги) - це точка, в якій всі похідні змінних за часом рівні нулю.

Підставивши ці значення, одержимо систему рівнянь

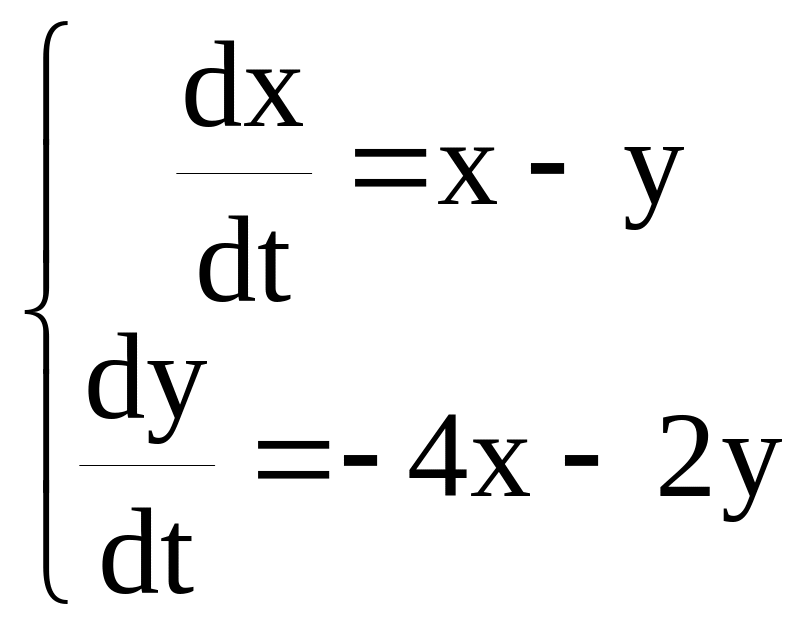(20)

Прирівнявши похідні до нуля, одержимо систему

(21)

розв’язком цієї системи буде

З системи (20) одержимо і, підставивши це рівняння в друге рівняння системи (21), одержимо

Позначаючи = , = , одержимо . (22)

Розв’язком рівняння такого типа є, x(t) = , тоді і . Тоді (3) прийме вигляд або Корені цього рівняння Оскільки вони дійсні і різних знаків, то фазовий портрет є сідлом.

Загальний розв’язок .

Виберемо для побудови траєкторії чотири різні набори констант, наприклад, с₁=1, с₂=1, тоді , тоді, і так далі. Змінюватимемо час від 0 з кроком 0,01 і знаходимо значення x і у для кожного набору констант, одержані точки нанесемо на графік і визначимо тип фазового портрета. З рисунка видно, що виходить сідло.