2.4 Системи диференціальних рівнянь

Системою диференціальних рівнянь називається сукупність рівнянь, що містять декілька невідомих функцій і їх похідні.

Розглядаються системи диференціальних рівнянь, що складаються із стількох рівнянь, скільки в них входить невідомих функцій, при цьому всі невідомі функції є функцією однієї незалежної змінної t.

Розв’язком системи диференціальних рівнянь називається сукупність функцій y_i(t) (i =1, ..., n), які при підстановці в рівняння обертають їх в тотожність.

Розглянемо систему диференціальних рівнянь наступного вигляду:

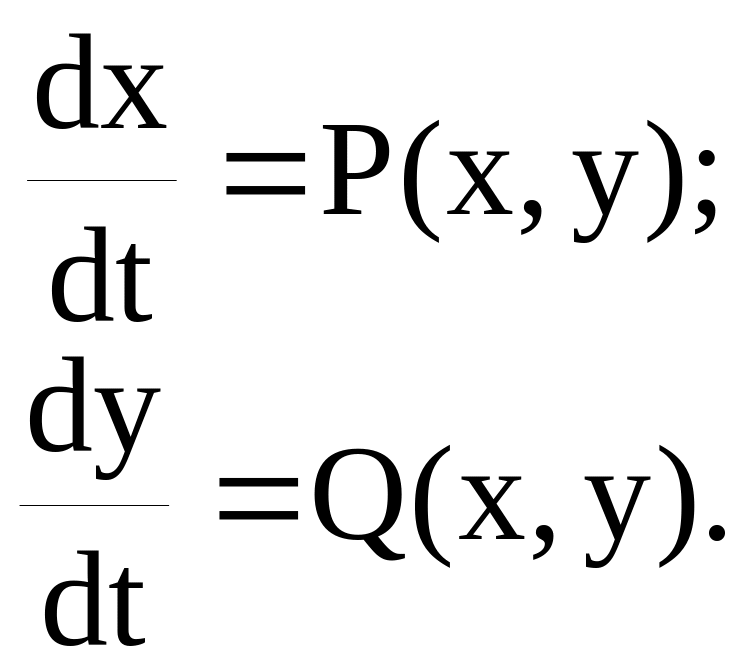
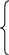(17)

Відзначимо, що в правих частинах рівнянь змінна t в явному вигляді не міститься. Такі системи називаються автономними динамічними системами. Основна геометрична інтерпретація системи (17) пов'язана з розглядом площини (х, у), так званою фазовою площиною.

Відзначимо, що ця інтерпретація істотно відрізняється від геометричної інтерпретації, описаної вище, її можна назвати кінематичною, оскільки в цій інтерпретації кожному розв’язку ставиться у відповідність рух точки по кривій, а не кривої в просторі.

Системи типу (17) використовуються для опису еволюційних процесів. Точка фазового простору визначає стан системи. Прикладений до цієї точки вектор з координатами dx/dt, dy/dt задає швидкість зміни стану. Точка, де цей вектор перетворюється в нуль (dx/dt = dy/dt = 0), називається положеннями рівноваги або особливою точкою системи (16).

Зіставимо геометричну інтерпретацію системи (17) в просторі X, Y, t з інтерпретацією на фазовій площині:

а) У кожну траєкторію фазової площини проектується сукупність інтегральних кривих в просторі X, Y, t. Ці криві виходять один з одного заміною t на t—C (рис. 5).

б) Якщо точка (а, b) є станом рівноваги системи Р(а, b)=0; Q(а, b)= 0, то інтегральна крива є прямою, паралельної осі t. Ця пряма проектується на площину (х, у) в єдину точку (а, b).

в) Якщо система має періодичний розв’язок з періодом , то в просторі х, у, t відповідна інтегральна крива є спіраллю з кроком . Ця спіраль проектується на фазову площину в замкнуту криву (рис. 5).

При проекції спіралі на площину (х,t) або (у,t) одержимо синусоїдальну криву, яка показує зміну змінної X(t) в часі.

Рисунок 5 – Поведінка рішень в просторі х. у, t і на фазовій площині

Обмежимося розглядом систем диференціальних рівнянь спеціального вигляду, так званих лінійних систем. У разі двох невідомих функцій x₁(t)_, x₂(t) лінійна система має вигляд

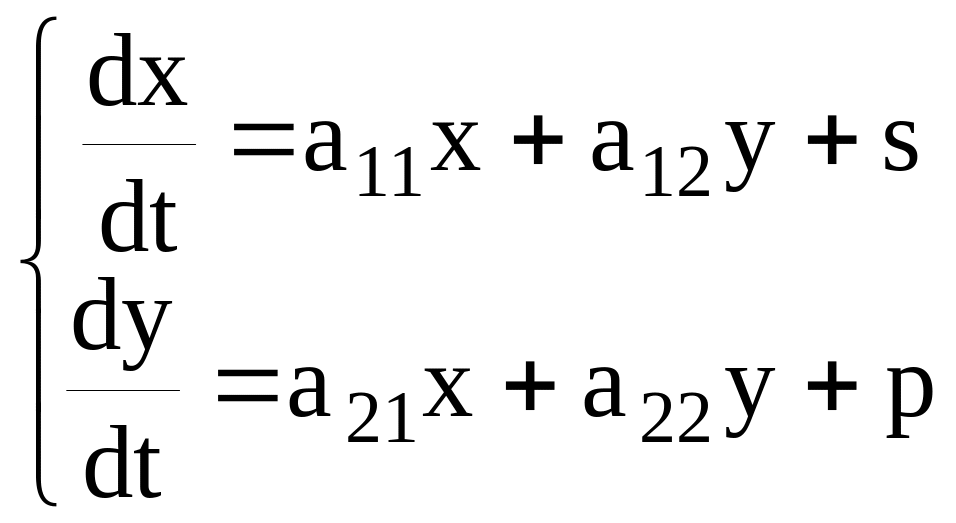(17)

Хай коефіцієнти а_ii в системі (17) постійні.

В цьому випадку для розв’язання системи можна використовувати методи лінійної алгебри. Дамо деяке уявлення про такі методи, обмежуючись системами двох рівнянь з двома невідомими, тобто системами вигляду (17).

При вивченні лінійних систем зручно використовувати матричні позначення. Умовимося скорочено записувати замість . Далі введемо матриці

Тоді систему (17) можна записати у вигляді одного матричного рівняння

(18)

Перш за все відмітимо, що система (17) має очевидний частковий розв’язок х₁(t)=0, x₂(t)=0. Цей розв’язок називається нульовим.

Інтерес представляють, звичайно, ненульові розв’язки. Шукатимемо такі розв’язки у вигляді х₁ = р₁ , х₂= р₂ , або, використовуючи матричний запис X=P _, де P=(р₁, р₂)^T - матриця (вектор) з постійними елементами р₁, р₂, не рівними одночасно нулю.

Маємо, очевидно, P . Підставляючи вирази для Х і в рівняння (18), одержимо P = P , звідки після скорочення на , знаходимо

AP=P (19)

Це рівняння говорить про те, що Р є власним вектором, а - власним значенням матриці А.

Хай ₁ і ₂ - корені характеристичного рівняння |А - E|=0. Припустимо спочатку, що ₁  ₂. Якщо P₁ - який-небудь власний вектор, відповідний ₁, а Р₂ - власний вектор, відповідний ₂, то формули X₁=P₁₁, X₂=P₂₂ визначають два часткових розв’язків рівняння (18). Загальний ж розв’язок, як можна продемонструвати, має вигляд:

де С₁, С₂ - довільні постійні.

Зрозуміло, числа ₁ і ₂ не обов'язково є дійсними. Може опинитися, що ₁ =  + i, і ₂ =  - i, де 0.

Нарешті, можливий випадок, коли корені ₁ = ₂ характеристичні рівняння співпадають. Замість двох часткових розв’язків Х₁ і Х₂ маємо тільки один розв’язок Х₁. Можна показати, що в цьому випадку вектор tX також є розв’язком; таким чином, і тут виходять два різних часткових розв’язка Х₁ і tX₁.

Для розмірності фазового простору, рівної 2 і 3 можна побудувати графічне представлення поведінки системи. Таке уявлення називається фазовим портретом системи.