
- • І. І. Скрильник Вступ
- •Лекція 1 Математичний апарат кібернетики (мак): елементи теорії множин. Аналіз систем на основі нечітких множин
- •1. Основні визначення
- •2. Логічні операції над множинами та їх властивості. Тотожні перетворення виразів
- •3. Алгебра множин. Пріоритет операцій
- •4. Поняття впорядкованої пари та декартового добутку множин
- •5. Нечіткі множини. Операції над нечіткими множинами та їх властивості
- •Основні характеристики нечітких множин Нехай та а – нечітка множина з елементами з універсальної множини е і множиною належностей м.
- •Приклади нечітких множин
- •Властивості операцій
- •6. Аналіз систем на основі нечітких множин
- •2. Булеві функції
- •3. Логічні операції та формули мл
- •4. Булева алгебра, тотожні перетворення
- •5. Висловлення. Предикати
- •6. Двійкова арифметика
- •7. Аналіз систем на основі математичної логіки
- •2. Типи скінченних графів
- •3. Орієнтовані графи, зважені графи
- •4. Суміжність, інцидентність графів, ізоморфізм графів
- •5. Маршрути, цикли графів
- •2. Бінарні відношення. Способи задавання перерізів
- •3. Властивості бінарних відношень
- •4. Функціональні відношення
- •5. Нечіткі відношення
- •Контрольні запитання
- •Лекція 5 Синтез систем на основі поняття про теорію автоматів
- •1. Загальна характеристика автоматів
- •Скінченні автомати
- •Представлення скінченних автоматів
- •4. Аналіз скінченних автоматів
- •5. Автомати Мілі та Мура
- •Продовження таблиці 5.5.1
- •Загальні властивості алгоритму
- •3. Приклади алгоритмів. Складність алгоритмів
- •4. Генетичний алгоритм
- •Генетичний алгоритм
- •Контрольні запитання
- •Лекція 7 Задачі оптимального керування. Методи розв’язання задач лінійного керування. Задачі на умовний екстремум
- •1. Поняття про математичне моделювання економічних задач
- •2. Різні форми задач лінійного програмування
- •Контрольні запитання
- •Лекція 8 Поняття про складні системи керування
- •1. Умови існування системи керування
- •2. Види зв’язків у системах керування
- •3. Види керування
- •4. Економічна система, її загальна характеристика
- •5. Системний підхід при дослідженні економічної системи
- •6. Економічна система як система керування
- •Контрольні запитання
- •Література
2. Булеві функції
Об’єкти з двома можливими станами характеризуються булевими змінними, здатними набувати лише два різних значення. Для позначення цих двох значень використовуються цифри 0 або 1 (чи букви “F” fals (неправда), “T” true (правда).
Відношення між булевими змінними представляються булевими функціями, які подібно числовим функціям можуть залежати від однієї, двох, n змінних (аргументів). Так, запис y=f(x1, x2,…,xn) означає, що y – функція аргументів x1, x2,…,xn.
Важлива особливість булевих функцій полягає у тому, що вони, як і їх аргументи, набувають свої значення із двохелементної множини {0,1}, або {T, F}, тобто характеризуються одним із двох можливих станів.
Функції невеликої кількості змінних можна задавати за допомогою таблиць, подібно до таблиць додавання та множення однорядних чисел. Для цього потрібно лише вказати значення функцій для кожної комбінації значень її аргументів. Основними у двозначній логіці є такі три функції.
Заперечення
функція y=f(x)
набуває
значення 1, коли x=0,
а значення 0, коли x=1.
Вона позначається
![]() (читається
не
x)
(таблиця
2.2.1).
(читається
не
x)
(таблиця
2.2.1).
Таблиця 2.2.1
-
x
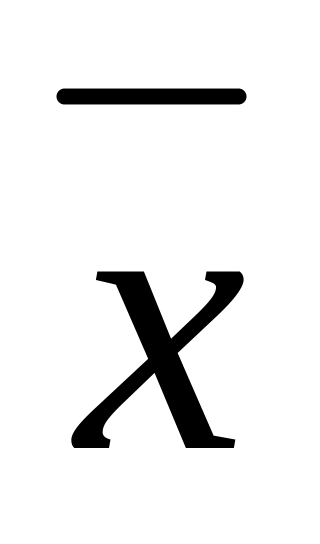
1
0
0
1
Диз’юнкція функція y=f(x1, x2), яка набуває значення 0 тоді і тільки тоді, коли обидва аргументи мають значення 0; вона позначається y=x1 x2 (читається “x1 або x2”) (таблиця 2.2.2).
Таблиця 2.2.2
-
X1
x2
0
1
0
0
1
1
1
1
x1 x2
Кон’юнкція – функція y=f(x1, x2),яка набуває значення 1 тоді й тільки тоді, коли обидва аргументи мають значення 1; вона позначається y=x1 x2 (читається “x1 та x2”) (таблиця 2.2.3).
Таблиця 2.2.3
-
X1
x2
0
1
0
0
0
1
0
1
x1 x2
3. Логічні операції та формули мл
Булеві функції
можна розглядати як логічні
операції над
величинами, котрі набувають два значення
– 0
або 1.
Заперечення
це одномісна операція, а дизюнкція
і конюнкція
двомісні операції. При цьому вирази x1
x2
, x1
x2,
![]() є логічними формулами. Більш складні
формули одержують заміщенням вхідних
змінних іншими логічними формулами, що
включаються у дужки.
є логічними формулами. Більш складні
формули одержують заміщенням вхідних
змінних іншими логічними формулами, що
включаються у дужки.
Наприклад,
x1=![]() ;
x2=
b
c, тоді
із x1
x2
маємо (
;
x2=
b
c, тоді
із x1
x2
маємо (![]() )
(b
c).
)
(b
c).
Кожна формула
визначає деяку булеву функцію. Її
значення при різних значеннях змінних
установлюється на основі таблиць. Так,
при а=0,
b=1,
c=0
маємо x1=![]() =
=![]() =1;
x2=
b
c=1
0 = 0; x1
x2=
(b
c)=1
0 =1. Аналогічно
отримуємо значення функції й при інших
комбінаціях значень аргументів.
=1;
x2=
b
c=1
0 = 0; x1
x2=
(b
c)=1
0 =1. Аналогічно
отримуємо значення функції й при інших
комбінаціях значень аргументів.
Дві функції (як і формули, котрі їх визначають) вважаються рівносильними, якщо при будь-яких значеннях аргументів ці функції, формули набувають однакові значення. Рівносильні функції з’єднуються знаком рівності. Рівносильність функцій перевіряється за таблицями основних операцій, причому необхідно порівнювати їх значення для всіх комбінацій значень змінних.
Наприклад,
1.
(x
y)![]() =
=![]()
z;
z;
2. ((x )y) (yx)=xy.
