5. Нечіткі множини. Операції над нечіткими множинами та їх властивості
Мабуть, найбільш вражаючим у людському інтелекті є здатність приймати правильні рішення в умовах неповної й нечіткої інформації. Побудова моделей наближених роздумів людини і використання їх у комп’ютерних системах є на сьогодні однією із найважливіших проблем науки.
Основи нечіткої логіки були закладені у кінці 60-их роках у роботах відомого американського математика Лафти Заде. Дослідження були пов’язані з наростаючим невдоволенням експертними системами. Хвалений “штучний інтелект”, який легко справлявся із задачами управління складних технічних комплексів, був безпорадний при найпростіших висловленнях повсякденного життя, наприклад, “Якщо в машині перед тобою сидить недосвідчений водій — тримайся від нього подалі”. Для створення дійсно інтелектуальних систем, здатних адекватно взаємодіяти з людиною, був необхідний новий математичний апарат, який би перекладав неоднозначні життєві твердження мовою чітких та формальних математичних формул. Першим серйозним кроком у цьому напрямі стала теорія нечітких множин, розроблена Заде. Його робота “Fuzzy Sets”, опублікована у 1965 році у журналі “Information and Control”, заклала основи моделювання інтелектуальної діяльності людини й стала початковим поштовхом до розвитку нової математичної теорії. Він же і дав назву цій новій галузі науки – “fuzzy logic” (fuzzy – нечіткий, розмитий, м’який). Подальші роботи професора Латфи Заде та його послідовників заклали фундамент для впровадження методів нечіткого управління в інженерну практику.
Апарат теорії нечітких множин, продемонструвавши низку багатообіцяних можливостей застосування – від систем управління літальними апаратами до прогнозування підсумків виборів, виявився разом з тим складним для втілення. Враховуючи наявний рівень технології, нечітка логіка зайняла своїє місце серед інших спеціальних наукових дисциплін – посередині між експертними системами й нейронними мережами.
Своє друге народження теорія нечіткої логіки пережила на початку 80-их років, коли декілька груп дослідників (США і Японії) серйозно зайнялися створенням електронних систем різного застосування, використовуючи нечіткі управляючі алгоритми. Теоретичні основи для цього були закладені у ранніх роботах Коско та інших вчених.
Третій період почався з кінця 80-их років і до цього часу. Цей період характеризується бумом практичного застосування теорії нечіткої логіки у різних сферах науки та техніки. До 90-го року з’явилося біля 40 патентів, що належали до нечіткої логіки (30 – японських). 48 японських компаній створюють лабораторію LIFE (Laboratory for International Fuzzy Engineering), японський уряд фінансує 5-річну програму з нечіткої логіки, яка включає 19 проектів – від системи оцінки глобального забруднення атмосфери і передбачення землетрусів до АСУ заводських цехів. Результатом виконання цієї програми була поява нових масових мікрочіпів, що базувалися на нечіткій логіці. Сьогодні їх можна знайти у пральних машинах та відеокамерах, цехах заводів і у моторах автомобілів, у системах управління складськими роботами й бойовими гелікоптерами.
У США розвиток нечіткої логіки йде по шляху створення системи для великого бізнесу і військових. Нечітка логіка застосовується в аналізі нових ринків, біржевій грі, оцінці політичних рейтингів, виборі оптимальної цінової стратегії та ін. З’явилися і комерційні системи масового застосування. Це привело до низки проблем, а саме:
нові архітектури комп’ютерів для нечітких обчислювань;
елементна база нечітких комп’ютерів та контролерів;
інструментальні засоби розробки;
інженерні методи розрахунку й розроблення нечітких систем управління і т.д.
Нехай
Е
є множина, А
–
підмножина Е:
.
Той факт, що елемент
належить
множині А
позначають
.
Для вираження цієї належності можна
використати й інше поняття –
характеристичну функцію –
, значення якої вказує, чи
належить множині А.
Приклад. Розглянемо скінченну множину з 5 елементів
та
.
Запишемо для кожного елемента із Е степінь його належності множині А
.
Це дозволяє представити А через всі елементи множини У, супроводжуючи кожний з них значенням його функції належності:
.
Отже,
нехай
–
універсальна множина,
,
а
–
деяка властивість. Звичайна (чітка)
підмножина
універсальної множини
,
елементи котрого задовольняють
властивість
,
визначаються як множина впорядкованої
пари
,
де
–
характеристична функція, що приймає
значення 1,
коли
задовільняє
властивість
,
і 0 –
в іншому випадку.
Нечітка
підмножина відрізняється від звичайної
тим, що для елементів
немає однозначної відповіді “ні”
відносно властивості
.
У зв’язку з цим, нечітка підмножина
універсальної множини
визначається як множина впорядкованої
пари
,
де
–
характеристична функція належності
(або просто функція належності), що
набуває значення на деякій впорядкованій
множині
(
наприклад,
–
на інтервалі).
Функція
належності вказує степінь (або рівень)
належності елемента
до підмножини
.
Множину
називають множиною належності. Якщо
,
тоді нечітка підмножина
може розглядатись як звичайна або чітка
множина.
Строге визначення поняття нечіткої множини, введене Заде.
Нехай
Е є множина , скнченна або ні, й x
–
елемент Е. Тоді нечіткою підмножиною А
множини Е називається множина впорядкованих
пар
,
де
–
ступінь належності x
в А.
Таким чином, якщо приймає свої значення у множині М значень функції належності або у множині належності, то можна сказати що x приймає значення в М за допомогою функції . Ця функція називається функцією належності.
Приклад
Нечітка
підмножина чисел x,
приблизно рівних даному дійсному числові
n,
де
(
–
множина дійсних чисел).
Розглянемо
множину
усіх чисел від 0
до 10.
Визначимо підмножину
множини
усіх дійсних чисел від 5
до 8,
коли
.
Покажемо функцію належності множини , ця функція ставить у відповідність число 1 або 0 кожному елементу в , залежно від того, належить цей елемент підмножині або ні. Результат покажемо на рисунку (рис. 1.5.1):
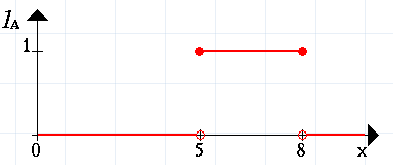
Рис. 1.5.1. Графічне зображення результату функції належності
Можна інтерпретувати елементи, що відповідають 1 як елементи, котрі знаходяться у множині , а елементи, що відповідають 0, як елементи, котрі не знаходяться у множині . Така концепція використовується у багатьох областях. Але існують ситуації, в яких цій концепції не вистачає гнучкості.
У цьому
прикладі опишемо множину людей. Формально
це можна записати так:
.
Оскільки,
взагалі, вік починається з 0, то нижня
границя цієї множини повинна бути нулем.
Верхню границю визначити складніше.
Спочатку встановимо верхню границю,
наприклад, рівну 20 рокам. Таким чином,
маємо В
як чітко визначений інтервал, буквально
.
Виникає питання: чому хтось у свій
двадцятилітній юбілей –
молодий, а зразу на наступний день уже
не молодий? Очевидно, це структурна
проблема, і якщо пересунути верхню
границю в іншу точку, то можна задавати
таке саме запитання.
Більш природний шлях створення множини В полягає в послабленні строгого поділу на молодих і на немолодих. Зробимо це, формулюючи не тільки чіткі судження “Так, він належить множині молодих людей” або “Ні, вона не належить множині молодих людей”, але й гнучкі формулювання, наприклад: “Так, належить множині доволі молодих людей”, “Ні, він не дуже старий”.
Розглянемо, як за допомогою нечіткої множини визначити вираз “Він ще молодий”.
У першому
прикладі ми кодували всі елементи
множини за допомогою 0
або 1.
Простим способом узагальнити цю концепцію
є введення значень між 0
та 1.
Реально можна навіть допустити нескінченне
число значень між 0
та 1,
в одиничному інтервалі
.
Інтерпретація чисел при співвідношенні всіх елементів множини стає тепер складнішою. Звичайно, число 1 відповідає елементу, що належить множині В, а 0 означає, що елемент точно не належить множині В. Усі інші значення визначають степінь належності до множини В. Для наочності покажемо характеристичну функцію множини молодих людей, як і в першому прикладі (рис. 1.5.2).
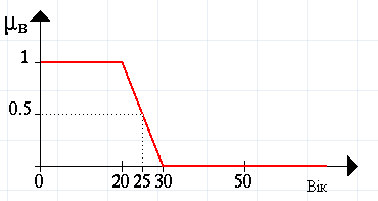
Рис. 1.5.2. Характеристична функція
Нехай E = {x1, x2, x3, x4, x5 }, M = [0,1]; A – нечітка множина, для якої
(x1)=0,3;
(x2)=0;
(x3)=1;
(x4)=0,5;
(x5)=0,9
.
Тоді A можна представити у вигляді:
A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 } або
A = 0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5 (знак “+” є операцією не додавання, а об’єднання) або
|
x1 |
x2 |
x3 |
x4 |
x5 |
A = |
0,3 |
0 |
1 |
0,5 |
0,9 |