3. Алгебра множин. Пріоритет операцій

Множина 2^U усіх підмножин універсальної множини U із заданими чотирма операціями (заперечення, перетин, об’єднання, різниця) становить алгебру множин.

У загальному випадкові алгебру множин може становити будь-який клас cr2^U підмножин універсальної множини U, замкнений відносно всіх чотирьох операцій.

Теорія множин, а також алгебра множин мають безліч корисних застосувань у програмуванні. Вона використовується для побудови систем управління базами даних під час побудови та організації роботи комп’ютерних мереж, зокрема мережі Інтернет. Ми щодня застосовуємо операції та закони алгебри множин, не замислюючись над цим. Наприклад, ми підраховуємо з множин задач, які потрібно розв’язати, множину розв’язаних і беремося до розв’язання решти. Із них ми, вірогідно, в першу чергу виберемо ті, які належать до множин легких. Ми готуємо сніданок, визначаючи перетин множин наявних продуктів з множиною продуктів, які нам подобаються. Все наше життя проходить серед множин, що якось взаємозв’язані.

Ми маємо достатньо операцій, щоб створювати складні алгебраїчні вирази. Для цього необхідно визначити, який пріоритет мають операції відносно одна одної. Пріоритет операцій в алгебрі множин такий:

1. . 2. .

3. . 4. .

Приклад

Визначити послідовність виконання операцій: .

З урахуванням пріоритетів це слід зробити так: .

4. Поняття впорядкованої пари та декартового добутку множин

Елементи множини можуть знаходитися у деяких відношеннях між собою або з елементами інших множин.

Відношення реалізують у математичних термінах на абстрактних множинах, реальні зв’язки  між реальними обєктами. Відношення застосовуються при побудові комп’ютерних баз даних, які організовані у виглядя таблиць даних. Зв’язки між групами даних у таблицях описуються мовою відношень. Самі дані обробляються і перетворюються за допомогою операцій, математично визначених для відношень. Такі бази даних називаються реляційними й широко застосовуються для збереження та обробки найрізноманітнішої інформації  виробничої, комерційної, статистичної тощо. Відношення також часто використовується у програмуванні. Такі складові структури даних, як списки, дерева тощо, звичайно використовуються для опису деякої множини даних разом з відношенням між елементами цієї множини.

Відношення між парами об’єктів називають бінарними. Прикладами бінарних відношень є рівність (=), нерівність (< або >), а також вирази: “бути братом”, “ділитися на (якесь) число”, “входити до складу (будь-чого)”. Для будь-якого бінарного відношення можна записати відповідне йому співвідношення, наприклад, x<y. У загальному вигляді можна записати xAy, де A – відношення, що встановлює зв’язок між елементом x із множини X(xX) і елементом y із множини Y(yY).

Ясно, що відношення повністю визначається множиною всіх пар елементів (x,y) для яких воно має значення. Тому будь-яке бінарне відношення А можна розглядати як множину впорядкованих пар (x,y).

Можна сказати, що функція f (y=f(x)) також є бінарним відношенням, бо вона кожному елементу x із множини X ставить у відповідність один і тільки один елемент із множини Y, тобто xfy.

Нехай маємо дві множини А та В (не обов’язково різні).

Декартовим добутком (добутком множин) є множина всіх упорядкованих пар елементів (a, b), із яких перший а належить множині А, а другий b – множині В.

Наприклад, A={a1,a2,a3,a4}, B={b1,b2}, тоді,

={a1,b1},{a1,b2},{a2,b1},{a2,b2},{a3,b1},{a3,b2},{a4,b1},{a4,b2}

Порядок пар може бути довільним, але розміщення елементів у кожній парі визначається порядком множин, що перемножуються, тому .

Операція множення множин узагальнюється на будь-яку їх кількість: .

У результаті одержуємо множину впорядкованих сукупностей елементів (a1,a2,…,an), яка називається кортеж, вектор.

Добуток множин не підлягає асоціативному та комутативному законам, але для нього виконується закон дистрибутивності відносно операцій об’єднання перетину та різниці:

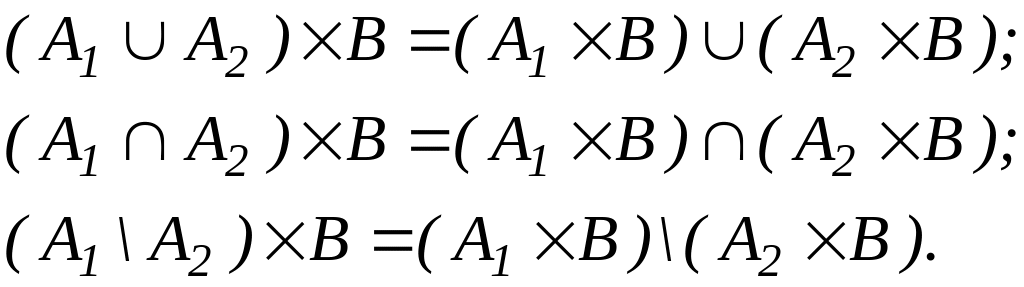
Для добутку n однакових множин А використовується означення через степінь , де А повторюється n разів.

Наприклад, A={a1,a2}, то

A3={(a1,a1,a1),(a1,a1,a2),(a1,a2,a1,),(a1,a2,a2), (a2,a1,a1),(a2,a1,a2),(a2,a2,a1,),(a2,a2,a2)}

Примітка. У результаті операцій об’єднання, перетину тощо завжди одержуємо множину, елементи котрої (якщо вона не пуста) належить вихідним множинам. Елементи добутку множин суттєво відрізняються від елементів співмножників і являють собою об’єкти другої категорії. Нехай N – множина натуральних чисел. Тоді буде множиною пар натуральних чисел (p,q), кожна з яких визначає найрізноманітніші об’єкти: дроби p/q, суми p+q номери будинків і квартир, пари учасників шахматного турніру. При цьому (p,q)(q,p).