2. Різні форми задач лінійного програмування

Розглянемо деякі математичні моделі задач планування й управління, що зводяться до задач оптимального керування.

Визначення найкращого складу суміші. Це одна з перших задач лінійного програмування.

Нехай нам відомо вміст необхідних для годування тварин поживних речовин у різних застосовуваних кормах. Відома також ціна одиниці кожного виду корму. Потрібно вибрати раціон – набір і кількість кормів – так, щоб кожна поживна речовина містилася у ньому в необхідній кількості і, крім того, щоб сумарні затрати на цей раціон були мінімальні.

Оптимальним планом є така впорядкованість чисел x₁, x₂, …, x_n , які повинні задовольняти наступні обмеження:

1. x₁ 0, x₂ 0, …, x_n 0.

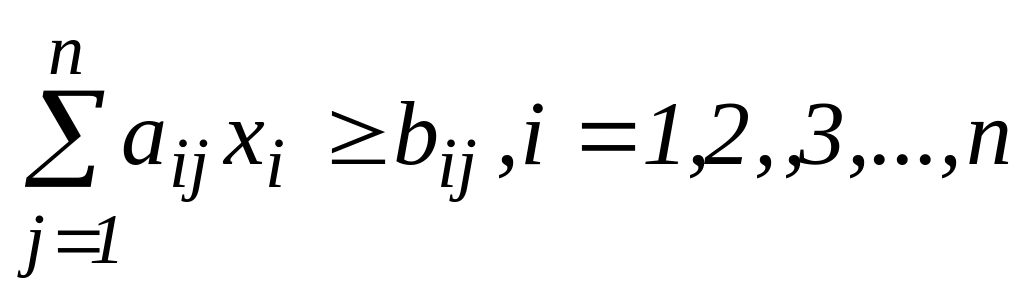2. та мінімізувати сумарні витрати, тобто 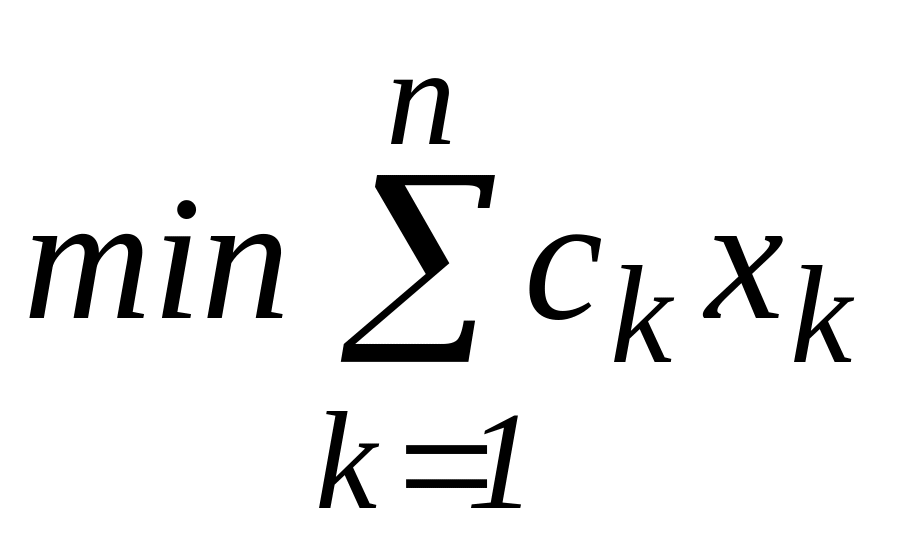, де

m – кількість різних необхідних поживних речовин;

n – кількість видів кормів;

а_іk – кількість одиниць і-й поживній речовині, що міститься в одиниці k-го виду корму;

b_i – мінімальна добова потреба в і-ї поживної речовини;

с_k – вартість одиниці k-ого виду корму;

x_k – кількість одиниць k-ого виду корму, що використовується у раціоні.

Аналогічний приклад про склад шифти. Відомо, що для одержання легованої сталі потрібно використати шихту певного хімічного складу. Багато інгредієнтів шихти достатньо дорогі. У той самий час у склад шихти входять малоцінні матеріали – чавун, лом, відходи. Виникає задача про вибір такої шихти, у склад якої входили б у заданій кількості необхідні хімічні речовини, а вартість її була б мінімальною.

Задача про оптимальний план випуску продукції. Ця задача виникає при складанні планів випуску продукції підприємством і тому має важливе практичне значення. Суть її полягає у наступному: нехай на підприємстві випускається n найменувань різних видів продукції. Позначимо через а_іj витрати i-го виду ресурсів (i= 1, 2, 3, …, m) на виробництво одиниці продукції j-го виду (j=1, 2, 3,…, n), через b_i — повні обсяги наявних ресурсів (i= 1, 2, 3, …, m), c_i — прибуток, одержаний підприємством при виготовленні й реалізації одиниці i-го виду продукту, а_і та А_і відповідно, наперед задану нижню й верхню границі за обсягом випуску i-го виду продукції. Потрібно скласти такий план випуску продукції, який би приносив найбільший прибуток підприємству і який би був технологічно здійсненним за всіма наявними ресурсами. Маємо таку математичну модель:

1. – технологічні обмеження.

2. – обмеження на обсяги окремих видів випускаючої продукції, що випускається і при цьому досягався б максимум.

– загальний прибуток від виробництва й реалізації продукції.

Оптимізація міжгалузевих потоків. Нехай маємо n галузей господарства, кожна із яких виробляє лише один специфічний вид продукції, причому кожний вид продукції використовується у виробництві в усіх n галузях. Нехай x_i – обсяг виробництва в i-й галузі, y_i – обсяг продукту і-го виду для позавиробничої потреби, a_ij – коефіцієнти прямих затрат продукції j-го виду на виробництво в і-й галузі одиниці продукції і-го виду, N_i – максимально можливий обсяг виробництва в і-й галузі, d_i – потрібна для позавиробничої потреби кількість продукції і-го виду, c_i – вартість одиниці продукції і-го виду.

Треба знайти такі можливі у заданих умовах обсяг виробництва x_i і такий план випуску кінцевої продукції y_i (i= 1, 2, 3, …, n), при якому максимізується загальна вартість виробленого кінцевого продукту.

Математична модель цієї задачі може бути подана у такому вигляді:

1. – обмеження на обсяги виробництва;

2. – обмеження на випуск кінцевого продукту;

3. – технологічні обмеження на випуски продукції.

Отже, потрібно знайти такі вектори x = (x₁, x₂, …, x_n) та y = (y₁, y₂, …, y_n), щоб

.

Серед таких задач також виділяють транспортну задачу, задачу Кантаровича про вибір виробничої програми, задачу про призначення, модель Неймана розширювальної економіки, оптимізація потоку газу в мережі та ін.

У найзагальнішому вигляді математично поставлена задача лінійного програмування формулюється таким чином: треба знайти такі значення змінних x₁, x₂, …, x_n, які задовольняють систему співвідношень виду

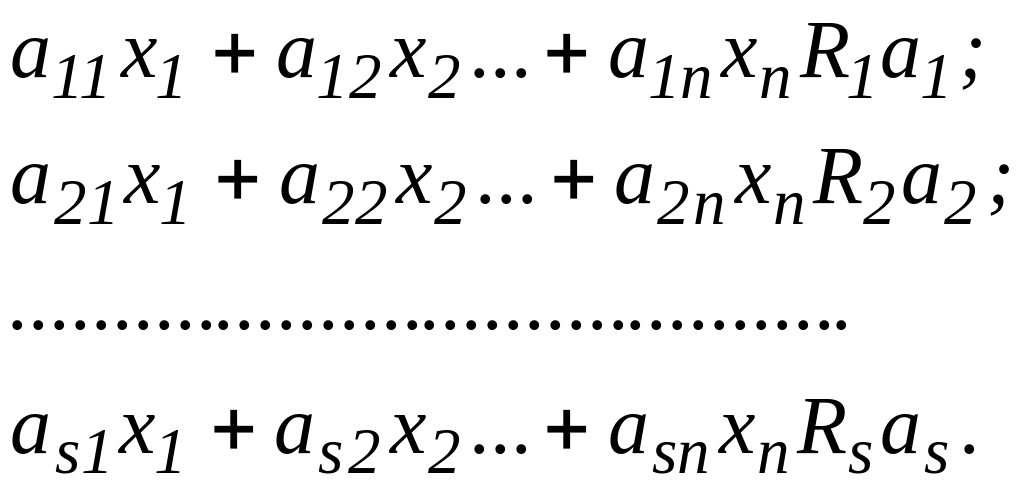
При цьому визначається найбільше (найменше значення) цільової функції

порівняно з її значеннями при всіх інших наборах значень змінних x₁, x₂, …, x_n, що задовольняють задану систему. Під R_i (i= 1, 2, 3, …, s) розуміють один із знаків =, , a_i, c_i, a_ij (i= 1, 2, 3, …, s; j=1, 2, 3, …, n) – задані дійсні числа. Всі ліві частини цих співвідношень та цільова функція лінійні відносно змінних, тому цю задачу називають задачею лінійного програмування.

3. Геометричний зміст задач лінійного програмування при n=2,3

У простішому випадку задача лінійного програмування містить усього дві змінних. Неважко одержати її геометричну інтерпретацію й розв’язати задачу геометрично. Нехай дана задача:

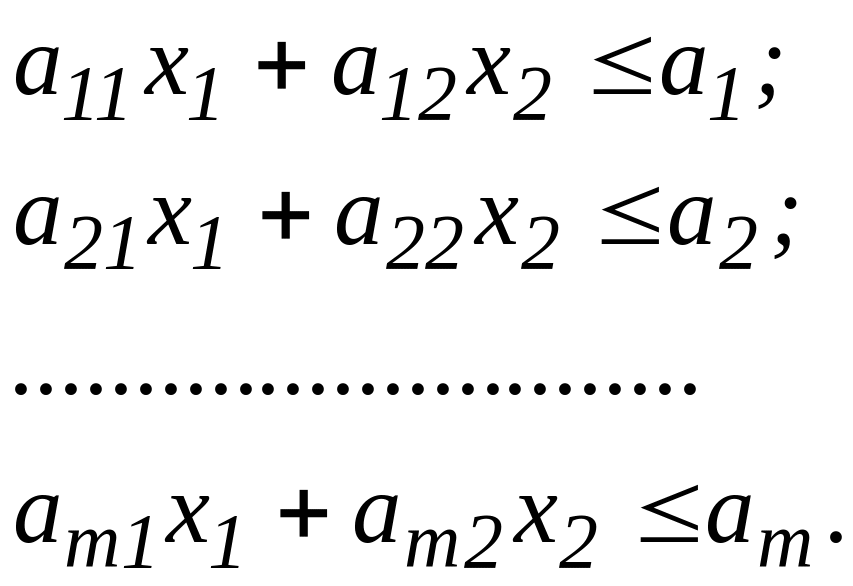
Уведемо на декартовій площині прямокутну систему координат і зіставимо кожну пару чисел (x₁, x₂) із точкою площини з координатами x₁ та x₂. Нерівність визначає на площині одну з двох півплощин, на котрі пряма розбиває площину. При цьому відповідна півплощина містить і граничну пряму . Щоб установити, яку саме півплощину визначає ця нерівність, достатньо підставити в неї координати однієї якої-небудь точки, що не лежить на граничній прямій. Якщо нерівність задовольняється, то шукана півплощина та, у котрій лежить узята точка, а якщо не задовольняється – то протилежна їй.

Приклади. Знайти допустимі області задач лінійного програмування з обмеженнями:

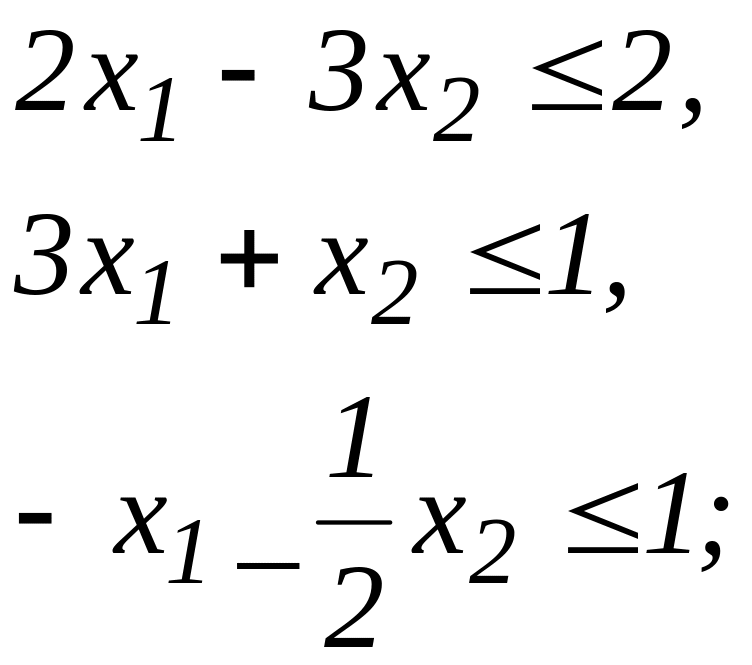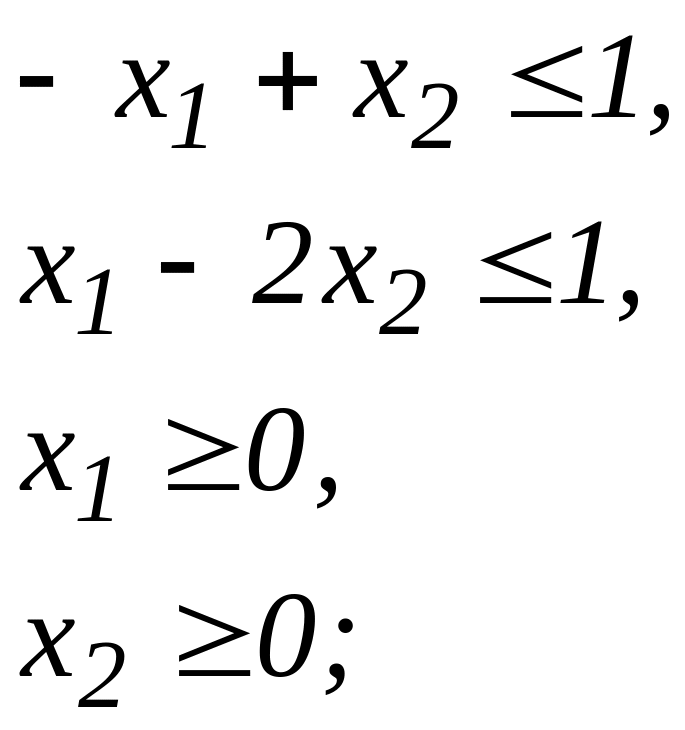1) 2) 3)

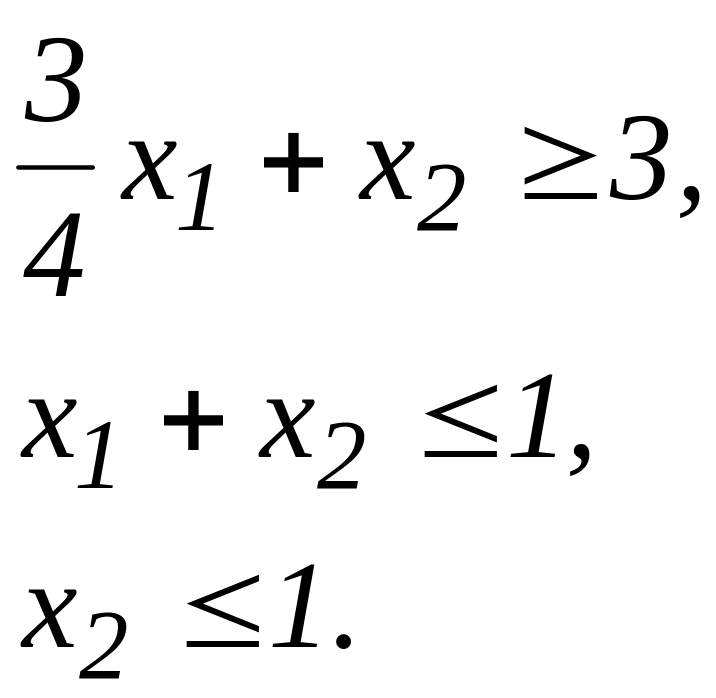
Третій приклад має допустиму область пусту. На цих прикладах ми бачимо, що допустима область задачі лінійного програмування може бути пустою (3), непустою й обмеженою (1), непустою й необмеженою (2). Якщо допустима область непуста, то вона являє собою деякий многокутник (може бути і необмежений). Умовно будемо називати многокутниками допустимі області й у тих випадках, коли вони виродилися в смугу, пряму, відрізок, точку. Очевидно, в усіх випадках відрізок, що з’єднує будь-які дві точки допустимої області, цілком міститься в ній. Області з такими властивостями називаються опуклими. Таким чином, допустима область задачі лінійного програмування, якщо вона не пуста, то вона є опуклою.

Як геометрично знайти оптимальні точки (тобто точки, що відповідають оптимальним рішенням цієї задачі)? Оптимальними є ті точки допустимої області, координати котрих надають цільовій функції найбільшого значення. Функція набуває одне і те ж значення, а в усіх точках прямої , де а – деяке дійсне число. Вважаючи а параметром, одержуємо сімейство паралельних прямих (так званих ліній постійного значення або ліній рівня функції ). Нас цікавлять, згідно з нашою задачею, ті точки допустимої області, котрі належать лінії рівня з найбільшим значенням а порівняно з його значенням для всіх інших ліній рівня, що перетинаються з допустимою областю.

Легко помітити, що значення а (а отже, і значення функції ) зростають необмежено, якщо переміщувати пряму у напрямі її нормалі — вектора с =(с₁, с₂), і спадають, якщо переміщувати її у напрямку

с =(-с₁, -с₂). Таким чином, щоб знайти оптимальні точки, потрібно переміщувати пряму у напрямку вектора с =(с₁, с₂), починаючи з якого-небудь фіксованого положення, при котрому вона перетинається з допустимою областю до тих пір, поки не перестане перетинатися з останньою. Перетин допустимої області з лінією рівня у тому її положенні, коли подальше переміщення дає пустий перетин, і буде множиною оптимальних точок задачі лінійного програмування. У випадку задачі мінімізації лінію рівня потрібно переміщувати у напрямі, протилежному напряму вектора с =(с₁, с₂).

Приклади

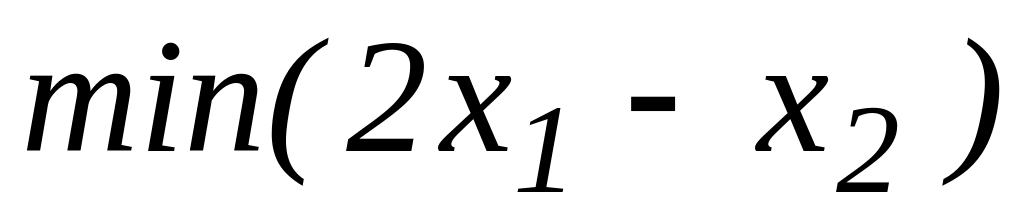1. Знайти за умов:

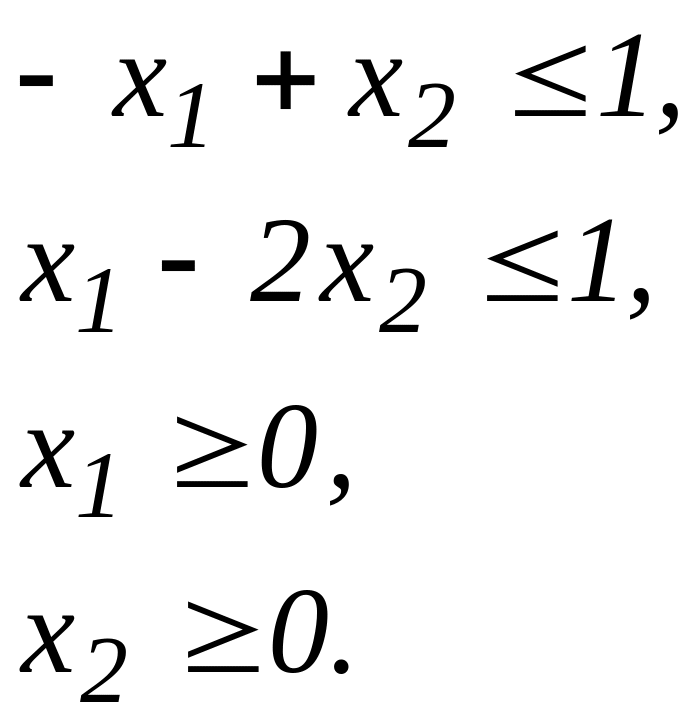
Побудуємо допустиму область, вектор с=(2, -1) і проведемо лінію рівня через точку О (0, 0). Тепер будемо переміщувати цю пряму паралельно самій собі у напрямі, протилежному с (задача на мінімум!). Очевидно, лінія рівня останній раз перетне допустиму область, коли пройде через точку А, координати котрої як точки перетину прямих x₁=0 та –x₁+x₂=1 дорівнюють (0, 1). Точка А(0,1) – єдина оптимальна точка (єдине оптимальне рішення), а f(0,1)=-1 – її оптимум.

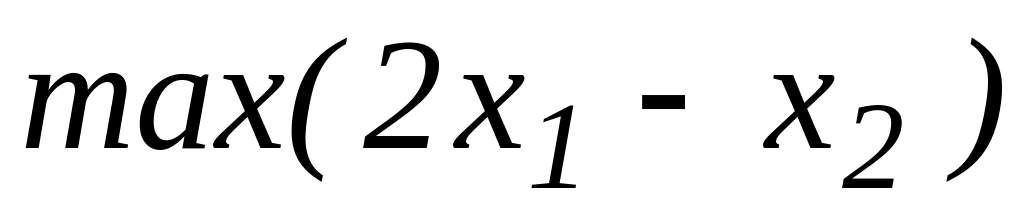2. Знайти за умов:

Ця задача відрізняється від попередньої тільки тим, що замість мінімуму нас цікавить її максимум. Отже, лінію рівня функції тепер потрібно переміщувати у напрямі вектора с. Очевидно, що як би довго ми не переміщували її в указаному напрямі, вона буде мати непустий перетин з допустимою областю. Тобто у допустимій області знайдуться точки, в котрих цільова функція має як завгодно велике наперед задане значення. Отже, ця задача не має розв’язку: цільова функція не обмежена (зверху) на допустимій множині.

Висновок

1) для n=2 геометрично очевидна наступна необхідна і достатня умова існування оптимального розв’язку

Задача лінійного програмування на максимум (на мінімум) тоді й тільки тоді має оптимальний розв’язок, коли її цільова функція обмежена зверху (відповідно знизу) в допустимій області;

2) допустима область і множина оптимальних точок – опуклі множини (якщо вони не пусті);

3) обмеженість цільової функції в допустимій області (відповідно зверху або знизу) є необхідною та достатньою умовою розв’язування;

4) оптимум задачі досягається у вершині допустимої області (якщо допустима область має вершини й задача має розв’язки).

Для випадку n=3 зазначені вище твердження залишаються справедливими, і вони мають місце для задачі лінійного програмування й у загальному випадку.

Алгоритм графічного методу розв’язання задач лінійного керування:

1. Будуємо область допустимих розв’язків.

2. Будуємо вектор с і перпендикуляр до нього (лінію рівня).

3. Рухаємо лінію рівня паралельно собі в напрямку вектора с, визначаючи останню точку.

4. Знаходимо координати x_max чи x_min та значення z.

Задача лінійного програмування полягає у відшукуванні на множині допустимих планів такого плану, який би мінімізував цільову функцію F. Такий план і буде оптимальним. Якщо кількість змінних системи обмежень та цільової функції у математичній моделі задачі лінійного програмування дорівнює 2 або 3, то таку задачу можна розв’язати графічно. Ознайомимося з графічним методом розв’язування на конкретних прикладах.

Задача. Процес виготовлення двох видів виробів заводом потребує, по-перше, послідовного оброблення на токарних та фрезерних верстатах і, по-друге, затрат двох видів сировини: сталі й кольорових металів. Дані про потреби кожного ресурсу на одиницю виготовленого виробу та загальні запаси ресурсів розміщені у таблиці 8. 3. 1. Прибуток від реалізації одиниці виробу А — 3 тис. грн., одиниці виробу В – 8 тис. грн. Визначити такий план випуску продукції, який забезпечує максимальний прибуток за умови, що час роботи фрезерних верстатів повинен бути використаний повністю.

Таблиця 7.3.1.

		Затрати на 1 виріб
		А	В	Ресурси
Матеріали	Сталь (кг)	10	70	320
	Кольорові метали (кг)	20	50	420
Обладнання	Токарні верстати (верстато-годин)	300	400	6200
	Фрезерні верстати (верстато-годин)	200	100	3400
Прибуток на виріб (у тис. грн.)		3	8

Розв’язання. Побудуємо математичну модель задачі. Позначимо через x кількість виробів виду А, через y – кількість виробів виду В. На виготовлення всієї продукції піде (10x + 70y) кг сталі та (20x + 70y) кг кольорових металів. Оскільки запаси сталі не перевищують 320 кг, а кольорових металів – 420 кг, то

Час оброблення всіх виробів на токарних верстатах дорівнює (300x + 400y) верстато-годин. З умови задачі випливає, що

Ураховуючи, що фрезерні верстати використовуються максимально, маємо

200x + 100y = 3400.

Отже, система обмежень цієї задачі така:

(1)

Загальний прибуток може бути виражений наступною функцією:

F = 3x + 8y. (2)

Виразимо y через x із рівняння 200x + 100y = 3400 і підставимо одержаний вираз замість y в останні обмеження та функцію

(3)

F = 3x + 8(34 – 2x) = -13x + 272. (4)

Здійснимо перетворення системи (3)

(5)

Очевидно, що F = 272 – 13x набуває найбільшого значення, якщо x = 16.

F_max = 272 - 13·16 = 64 (тис. грн.).

Розв’яжемо цю задачу графічно.

Математична модель цієї задачі представляється системою обмежень (1),

на множині розв’язків якої потрібно знайти найбільше значення цільової функції

F = 3x + 8y. (6)

Необхідно знайти множину точок площини (множину допустимих планів), координати яких задовольняють систему обмежень (1) (рис. 8.3.1). Нерівності та показують, що множина допустимих планів розміщена у першому квадранті. Інші нерівності системи задають у першому квадранті фігуру OACKL (вона позначена штрихуванням). Рівняння 2x + y = 34 із прямокутника OACKL виділяє множину допустимих планів. Це точки відрізка EN. Серед точок цього відрізка виберемо таку, в котрій цільова функція F досягає максимального значення. Для цього за допомогою рівняння 3x + 8y = С будуємо декілька прямих (лінії рівня F), надаючи C довільного значення (наприклад, 120, 240 й ін.). Так одержуємо сімейство паралельних між собою прямих. Із збільшенням значення С пряма 3x + 8y = C буде рухатися вгору-направо (рис. 8.3.1). Останньою точкою відрізка EN, якої торкнеться пряма

3x + 8y = C, буде точка E. Визначимо її координати.

Для цього достатньо розв’язати систему рівнянь

(7)

оскільки точка E є перетином прямих 2x + y =34 та 2x + 5y = 42. Розвязком системи (7) є пара (16; 2).

Цей розв’язок є оптимальним планом.

F_max = 3·16 + 8·2 = 64.

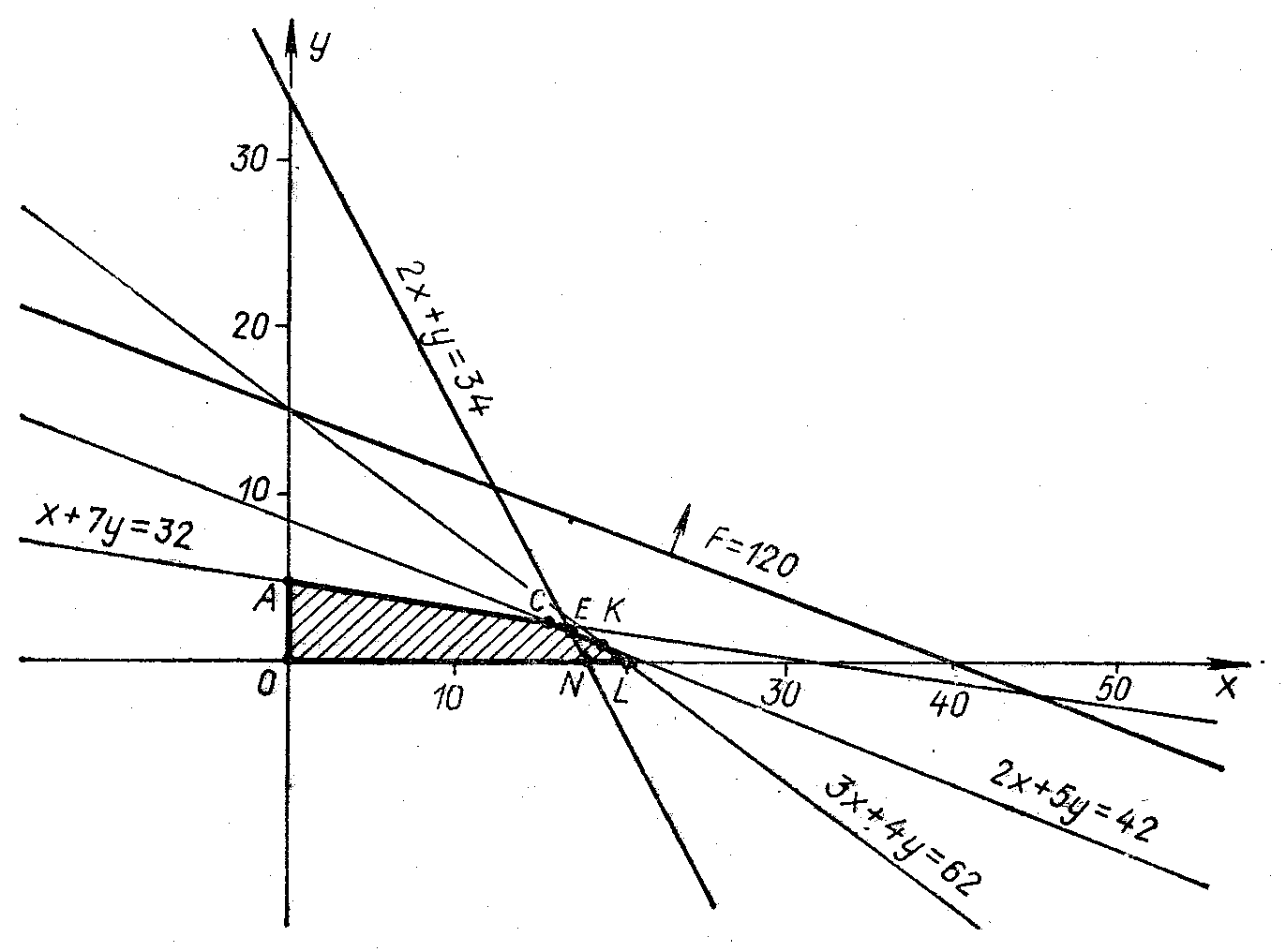
Рис. 7.3.1. Графічний розв’язок задачі