2. Загальні властивості алгоритму

Багатий досвід розроблення та застосування алгоритмів підказує низку їх загальних властивостей:

• дискретність і скінченність алгоритму (результативність);

• детермінованість алгоритму (розпізнаваність та однозначна визначеність);

• спрямованість алгоритму;

• масовість алгоритму (універсальність);

• елементарність кроків алгоритму.

Дискретність алгоритму. Будь-який алгоритм можна розглядати як процес послідовної побудови величин, що відбувається у дискретному часі за визначеним записом (програмою). У початковий момент задаються вихідні дані, а у кожний наступний момент за програмою одержуємо сукупність наступних величин. Тобто програма йде крок за кроком, незалежно від часу.

Детермінованість алгоритму. Визначеність. Сукупність величин, стримуваних у якийсь (не початковий) момент часу, однозначно визначається сукупністю величин, одержаних у попередні моменти часу. Перетворення на кожному кроці повинні бути однозначно визначеними.

Спрямованість алгоритму (результативність). Якщо спосіб отримання наступної величини з будь-якої заданої не є результативним, то повинна бути вказівка, що саме потрібно вважати результатом алгоритму. Інакше кажучи, алгоритм через скінченну кількість тактів часу (кроків) повинен привести до зупинення, яке свідчить про досягнення потрібного результату. Тобто якщо при певних вхідних даних алгоритм не може дійти до кінця за скінченну кількість кроків, то цей алгоритм не може дати точного розв’язку задачі.

Масовість алгоритму. Алгоритм служить для розв’язування цілого класу задач, при цьому початкова сукупність величин може вибиратися з деякої множини. Наприклад, у алгоритмі Евкліда числа a та b вибираються з нескінченної множини цілих чисел. У математиці проблема вважається розвязаною, якщо для неї знайдений загальний алгоритм. Тобто це можливість розвязання цілого класу задач, а не якоїсь конкретної.

Елементарність кроків алгоритму. Запис про одержання наступної сукупності величин із попередньої має бути простим і локальним. Це означає, що відповідна операція повинна бути елементарною для виконання алгоритму (чи людиною, чи машиною).

3. Приклади алгоритмів. Складність алгоритмів

Загальну схему алгоритму можна подати у такому вигляді (рис. 6.3.1):

Рис. 6.3.1. Блок-схема алгоритму

Для візуалізації роботи алгоритму можна використовувати блок-схеми. Елементи блок-схеми:

Приклад 1

Скласти алгоритм і зобразити за допомогою блок-схеми розв’язання квадратного рівняння (рис. 6.3.2).

Рис. 6.3.2. Блок-схема розв’язування квадратного рівняння

1. Визначаємо a, b, c.

2. Обчислюємо детрмінант .

3. Детермінант порівнюємо з 0.

4. Якщо D>=0, то рівнянн має два розвязки .

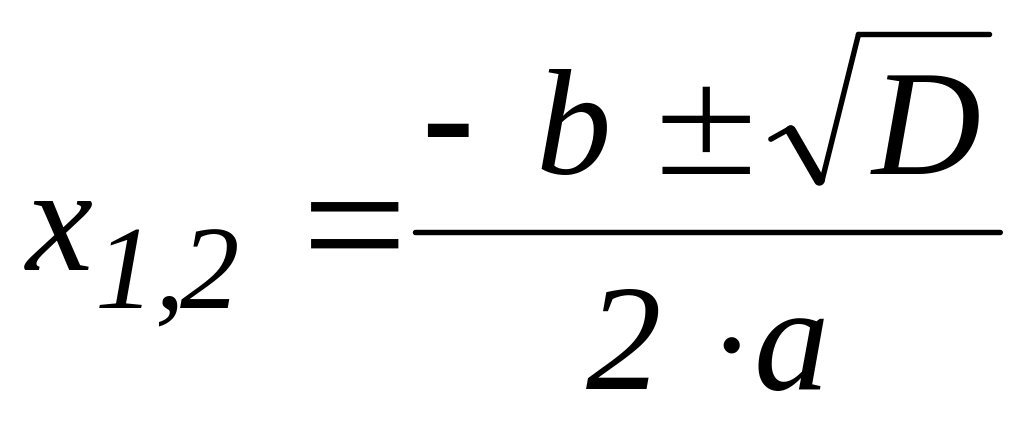5. Завершуємо роботу програми.

6. Якщо D < 0, то рівнянн не має розв’язків.

7. Завершуємо роботу програми.

Приклад 2

Відсортувати у порядку зростання задану послідовність чисел 3 –1 0 1 8 6 5 -5.

Ідея алгоритму:

1. беремо перше число;

2. порівнюємо його за величиною з наступним числом;

3. якщо перше число більше від наступного, то переставляємо ці числа місцями;

4. збільшимо лічильник i на одиницю та переходимо до наступного числа;

5. кроки 2-4 повторюємо до тих пір, поки змінна і буде рівною n.

Цикл повинен повторюватися nn разів (n — кількість елементів у масиві). Крім масиву, будемо використовувати додаткову змінну k для перестановки чисел. Перестановку чисел здійснюватимемо таким чином (рис. 6.3.3):

k = A[i];

A[i] = A[i+1];

A[i+1] = k.

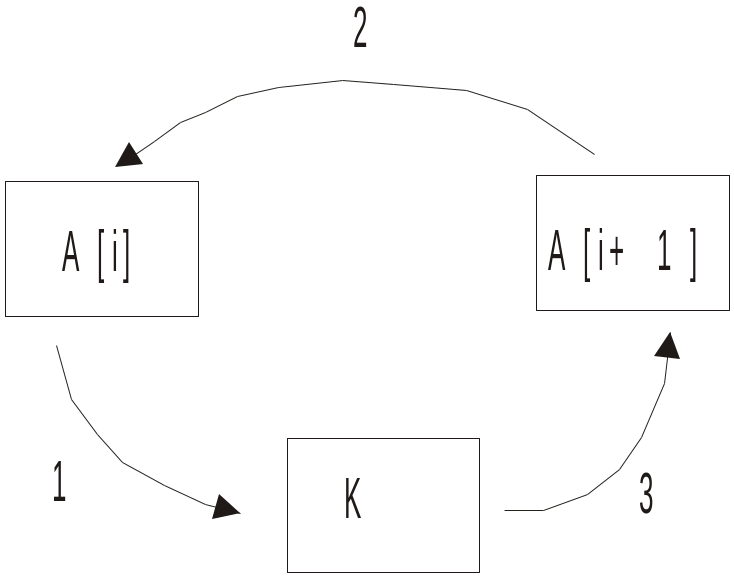
Рис. 6.3.3. Схема перестановки чисел

Вхідний масив A[1] …A[n] – послідовність довжини n, що підлягає сортуванню. Блок-схема алгоритму має такий вигляд (рис. 6.3.4):

Рис. 6.3.4. Блок-схема сортування послідовності чисел

Приклад 3. Знайти максимальне число в послідовності чисел.

Маємо наступний алгоритм:

1. беремо перше число;

2. нехай вибране перше число є максимальним;

3. кожне число послідовності порівнюємо із цим максимальним числом;

4. як тільки з’явиться число, більше від максимального, то йому надаємо значення максимального числа;

5. переходимо до пункту 3;

6. як тільки максимальне число стане більшим від n, то зупиняємо програму.

Крім масиву чисел, використовується змінна max. A[1] …A[n] – послідовність довжини n. Блок-схема має такий вигляд (рис. 6.3.5)

Рис. 6.3.5. Блок-схема знаходження максимального значення послідовності чисел

Розглядаючи різні алгоритми розв’язку однієї й тієї ж задачі, слід проаналізувати, скількох обчислювальних ресурсів вони потребують, та вибрати найбільш ефективний алгоритм. Безумовно, ефективність залежить від вибору обчислювальної моделі. Розрізняють складність самого алгоритму і складність його опису (реалізації).

Складність опису алгоритму – це величина, що характеризує довжину опису алгоритму. Складність алгоритму (складність обчислення алгоритму) – це функція, що дає числову оцінку тривалості роботи алгоритму з моменту надходження на його вхід початкових даних до моменту одержання алгоритмом вихідних даних. Для оцінювання складності алгоритмів існує багато критеріїв. Найчастіше розглядається оцінка часу повного розв’язку задачі й зростання місткості пам’яті при збільшенні обсягу вхідних даних.

Розміром задачі називається число, яке виражає міру кількості вхідних даних. Наприклад, розміром множення матриць може бути найбільший розмір матриць-чинників. Розміром задачі на графі може бути кількість ребер даного графа.

Час, котрий витрачає алгоритм, як функція розміру задачі, називається часовою складністю цього алгоритму. Обсяг пам’яті, що використовує алгоритм, як функція розміру задачі, називається місткісною складністю цього алгоритму.

При заданих обмеженнях пам’яті та швидкості комп’ютера складність алгоритму визначає, врешті-решт, розмір задач, котрі можна розв’язати за цим алгоритмом.