Продовження таблиці 5.5.1

						0	1	1	1
						1	0	0	1

Діаграму станів, що відповідає цьому автомату, подано на рисунку 5.5.1.

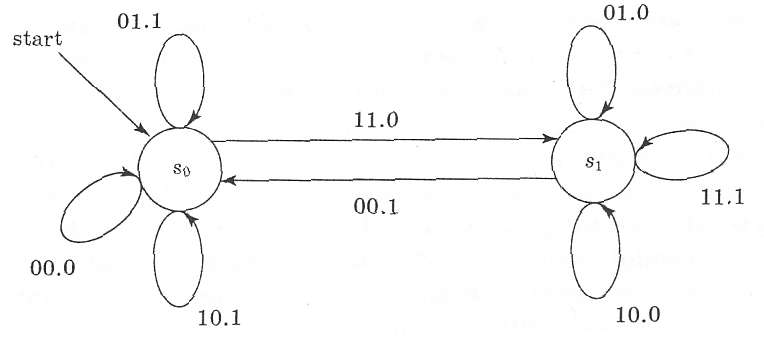
Рис. 5.5.1. Скінченний автомат Мілі для додавання

Біля кожної стрілки переходу вказано вхідну інформацію і вихідний сигнал. Наприклад, запис 01.1 біля петлі у стані означає, що коли на вхід із станом надходить пара бітів 01, то на вихід необхідно видати 1 і як наступний стан зберегти . Розглянемо роботу автомата. Якщо, наприклад, поточний стан – і на вхід поступає 01, наступний стан буде , а вихід – 0. Відбувається додавання 0+1+1=(10)₂. Тому вихідний сигнал – 0, а перенесення 1 визначає наступний стан .

Приклад 2

Побудувати автомат Мура, який на виході друкує 1, якщо кількість одиниць, прочитаних автоматом у вхідному рядку, ділиться на 3, і друкує 0 у протилежному випадку (автомат також друкує 0, якщо не прочитано жодної одиниці у початковому стані ). Вхідний алфавіт автомата . Назвемо цей автомат . Визначимо стани автомата: – початковий стан, – прочитано кількість одиниць, що дає при діленні на 3 у залишку 1, – прочитано кількість одиниць, що дає при діленні на 3 у залишку 2, – прочитано кількість одиниць, кратне 3. Звичайно, що вихідну інформацію у такому автоматі можна поставити у відповідність станам. Побудуємо таблицю переходів (табл. 5.5.2).

Таблиця 5.5.2

Таблиця станів автомата

	0	1
			0
			0
			0
			1

Припустимо, на вхід автомата надійшов рядок 0001010100. Розглянемо, яку вихідну інформацію видасть автомат. Побудуємо відповідну таблицю (табл. 5. 5. 3). Після прочитання рядка 0001010100 автомат друкує 1, тобто кількість одиниць, що прочитав автомат у вхідному рядку, ділиться на 3.

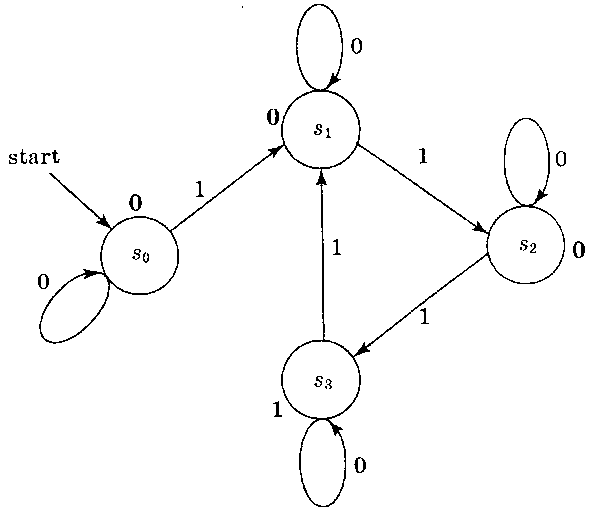
Рис. 5.5.2. Автомат Мура

Таблиця 5.5.3

Вхідна інформація автомата

Прочитаний рядок
0		0
00		0
000		0

Продовження таблиці 5.5.3

0001		0
00010		0
000101		0
0001010		0
00010101		1
000101010		1
0001010100		1

Контрольні запитання

1. Для дослідження яких питань використовуються автомати?

2. Поясніть принцип дії та побудову кожної частини автомата.

3. Що включає такт роботи автомата?

4. Чим відрізняються детерміновані й недетерміновані скінченні автомати?

5. Дайте визначення автоматів Мілі та Мура.

Лекція 6

Поняття про алгоритм. Роль алгоритмів у системах керування

1. Визначення агоритму, його види.

2. Загальні властивості алгоритму.

3. Приклади алгоритмів. Складність алгоритмів.

4. Генетичний алгоритм.

1. Визначення агоритму, його види

З давніх часів у математиці склалося інтуїтивне уявлення про алгоритм. Алгоритм – як формальний запис, який визначає сукупність операцій і порядок їх виконання для розв’язування всіх задач певного типу.

Кожний ознайомлювався з алгоритмами ще в школі. Правила, за котрими виконуються арифметичні дії, є найпростішими прикладами алгоритмів. Сам термін “алгоритм” походить від імені середньовічного узбецького математика Аль-Хорезмі, який ще у IX ст. формулював такі правила. В своєму розвитку математика нагромадила величезну кількість різних алгоритмів. Одержуючи відповідну інтерпретацію у конкретних додатках, вони становлять значну і найбільш вагому частину математичного апарату, використовуваного у техніці.

У наш час поняття алгоритму піддавалося глибокому вивченню та уточненню, головним чином, у зв’язку з проблемою алгоритмічної нерозвязності. Справа у тому, що намагання розвязати ряд задач виявилися матними, незважаючи на численні спроби видатних математиків. Наприклад, до цього часу не вдалося знайти алгоритм для розв’язання діафантових рівнянь, залишилася нерозв’язаною проблема чотирьох фарб у теорії графів. У зв’язку із цим виникло припущення про те, що далеко не для будь-якого класу задач можлива побудова алгоритму для розв’язування.

Існують два види алгоритмів: числові алгоритми, логічні алгоритми. Алгоритми, які зводять рішення поставленої задачі до арифметичних дій над числами, називаються числовими алгоритмами. Традиційним прикладом є відомий алгоритм Евкліда для знаходження найбільшого загального дільника двох заданих цілих додатних чисел a та b.

Алгоритм Евкліда полягає у такій системі послідовних дій:

1. Визнач a та b і переходь до наступної.

2. Порівняй визначені числа (a = b, a < b, a > b) і переходь до наступної.

3. Якщо визначені числа рівні, то кожне з них дає шуканий результат, якщо ні – переходь до наступної.

4. Якщо перше визначене число менше від другого, перестав їх місцями і переходь до наступної.

5. Відніми друге число від першого та визнач два числа – від’ємник і остачу– і переходь до 2.

Після п’ятої вказівки потрібно кожного разу повертатися до другої доти, доки не буде виконана третя вказівка. Заздалегідь ми не можемо вказати, скільки потрібно буде таких циклічних переходів, але нам зрозуміло, що для будь-яких двох чисел мета буде досягнута за скінченну кількість кроків.

Логічні алгоритми містять записи, що належать не до цифр, а до об’єктів будь-якої природи. Прикладом логічних алгоритмів може служити алгоритм пошуку шляху в скінченному лабіринті.