2. Скінченні автомати

Скінченний автомат складається тільки з вхідної стрічки та керуючого пристрою зі скінченною пам’яттю. Кількість його станів скінченне. Керуючий пристрій може бути детермінованим або недетермінованим, але вхідна головка – одностороння, що зміщується вправо.

Скінченний автомат – це структура виду M = (X, Y, S, f, g, F), котра визначається як система із скінченною множиною вхідних символів (сигналів) X={x_1, x_2, x_3,…, x_p}, із скінченною множиною вихідних символів Y={y_1, y_2, y_3…, y_q}, скінченною множиною станів S = {s₁, s₂, s₃,…, s_r} та двома характеристичними функціями:

f – відображення множини у множину , що визначає вибір наступного стану;

g – відображення множини у множину , що встановлює вихідний символ;

– множина завершальних станів;

 – номер такту.

Функції (, ) задають деякі відношення між елементами цих множин (рис. 6.2.1).

Рис. 5.2.1. Блок-схема скінченного автомата

Відповідно кінцевий автомат можна позначити M = (X, Y, S, , ). У двійковому структурному алфавіті p = 2ⁿ, q = 2^m, r = 2^k. Загальна блок-схема кінцевого автомата може бути подана у вигляді комбінаційної схеми, що реалізує функції ,  та пам’яті, яка зберігає на один такт попередній стан автомата (рис. 5.2.2).

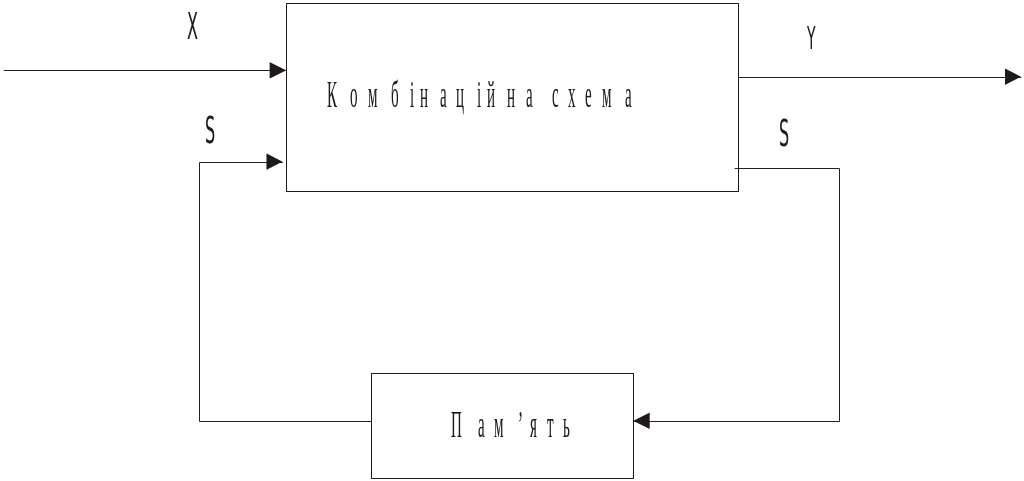
Рис. 5.2.2. Блок-схема скінченного автомата

Ці функції можна розглядати як деяке відображення множини X S (чи його підмножини D  X  S) відповідно на множини X та Y. Якщо X  S  S і

X S  Y – автомат називається повним; X S  S – називається повним по переходах. Якщо функції ,  визначені не для всіх наборів із множини X S – автомат називається неповним або частково визначеним.

Ясно, що послідовні схеми повинні мати здатність зберігати попередній стан до наступного такту, такі автомати називають автоматами з пам’яттю чи послідовними машинами. Як пам’ять можуть бути використані елементи затримки, на виходах котрих повторюються вхідні впливи із зсувом у часі на інтервал між тактами t. Інтервал між тактами може бути різним. Широко застосовуються також різні запам’ятовуючі елементи, наприклад тригери, здатні зберігати стани на виходах до тих пір, поки він не змінюється у результаті дії на їх входи. Такі види автоматів називаються дискретними.

3. Представлення скінченних автоматів

Автомат може бути заданий різними способами, наприклад, словесним описом його функціонування або переліченням елементів множин X, Y, S з указаним відношенням між ними. В аналізі та синтезі кінцевих автоматів використовують стандартні форми представлення: таблиці, графи, матриці. Елементи множин X, Y, S зручно пронумерувати порядковими числами, починаючи з нуля.

Приклад

X = {0, 1, 2, 3};

Y = {0, 1};

S = {0, 1, 2, 3}.

Представимо функції ,  двома таблицями, рядки яких відповідають станам, а стовпці – входам. Перша таблиця називається таблицею переходів, відповідає функції , і її клітинки заповнюються номерами станів та стану в даний тактовий момент.

Друга таблиця називається таблицею виходів, що відповідає функції , і її клітинки заповнюються номерами виходів y() у той же момент. Наприклад, для заданих X, Y, S такі таблиці можуть мати такий вигляд (табл. 5.3.1, табл. 5.3.2, табл. 5.3.3):

Таблиця 5.3.1

s() \X()	0	1	2	3
0	3	2	1	3
1	3	2	1	3
2	3	2	2	3
3	3	0	0	1

Таблиця 5.3.2

s() \X()	0	1	2	3
0	0	0	0	0
1	1	0	0	1
2	1	0	1	1
3	0	0	1	1

Таблиця 5.3.3

Загальна таблиця переходів:

s() \X()	0	1	2	3
0	3/0	2/0	1/0	3/0
1	3/1	2/0	1/0	3/1
2	3/1	2/0	2/1	3/1
3	3/0	0/0	0/1	1/1

Граф автомата будується таким чином: його вершини відповідають станам, а направлені дуги позначаються як диз’юнкція входів, під дією яких здійснюється перехід з одного стану в інший за напрямом дуги. У знаменниках записуємо номери виходів, відповідні цим переходам (рис. 5.3.1).

Рис. 5.3.1. Граф скінченного автомата

Оскільки із стану 0 автомат переходить у стан 1, 2, 3, то з вершини 0 графа виходять дуги з вершини 1, 2, 3. При цьому перехід із стану 1 відбувається під дією 2 та йому відповідає вихід 0, тому дуга з вершини 0 в 1 позначається як 2/0. Перехід у стан 2 здійснюється під дією 1, і йому відповідає вихід 0, тому дуга з вершини 0 у 2 помічається як 1/0. Переходи у стан 3 відбуваються під дією 0 та 3, і їм обом відповідає вихід 0, тому дуга з вершини 0 в 3 позначається як дизюнкція 0/03/0.

Аналогічно визначаються й інші дуги графа. Петлі відповідають переходам, при яких стан не змінюється. Так цей автомат переходить із стану 2 у 2 під впливом 1 і 2, котрим відповідають виходи 0 та 1. Отже, петля при вершині 2 помічається як диз’юнкція 1/02/1.

Матриця з’єднання автомата М (або матриця переходів) являє собою квадратну матрицю, у якій номери рядків і стовпців відповідають номерам станів.

Клітинка матриці на перетині і-го рядка та j-го стовпця заповнюється диз’юнкцією пар “вхід–вихід”, котра приписана дузі графа, що виходить із і-ї та j-ї вершин. За відсутності такої гілки клітинка заповнюється 0 або залишається пустою. Отже, в нашому випадку маємо (табл. 5.3.4).

Таблиця 5.3.4

Матриця з’єднання автомата М

0	1	2	3
	2/0	1/0	0/03/0	0
	2/0	1/0	0/13/1	1
		1/02/1	0/13/1	2
1/02/1	3/1		0/0	3