3. Властивості бінарних відношень

Нехай А – бінарне відношення у множині X. Визначимо основні властивості таких відношень, які повинні виконуватися для всіх (x_i, x_j)A. Говорять, що AXX:

1. Рефлексивність

Бінарне відношення А називається рефлексивним, якщо AE (E – тотожне відношення), тобто воно завжди виконується між обєктом і ним самим:

XAx.

Приклад: рівність, самообслуговування.

2. Антирефлексивність

Бінарне відношення А називається антирефлексивним, якщо AE=, тобто може виконуватися лише для об’єктів, що не співпадають: із x_iAx_j слідує, що x_ix_j .

Приклад: “x є брат y”, але не можна сказати, що x є сам собі брат; строга нерівність, бути старшим.

3. Симетричність

Бінарне відношення А називається симетричним, якщо А=А^-1, тобто при виконанні x_iAx_j  x_jAx_i.

Приклад: відстань між двома точками, “бути братом”.

4. Антисиметричність

Бінарне відношення А називається антисиметричним, якщо АА^-1E, тобто відношення x_iAx_j та x_jAx_i виконуються одночасно тоді й тільки тоді, коли x_i=x_j.

Приклад: нестрога нерівність , включення.

5. Транзитивність

Бінарне відношення АА називається транзитивним, якщо АА, тобто з xAx_j та x_jAx_k x_iAx_k виконується умова (“бути дільником”, “бути родичем”).

6. Еквівалентність

Бінарне відношення, яке одночасно є рефлексивним, симетричним, транзитивним.

4. Функціональні відношення

Функціональна залежність між змінними, або функція, є частковим випадком відношення.

Відношення між множинами X та Y ( ) є функціональним, якщо всі його елементи (впорядковані пари) різні за першим елементом: кожному або відповідає тільки один елемент , такий, що , або такого елемента взагалі не існує.

Матриця функціонального відношення, що задане на скінченних множинах X та Y , містить не більше відоднієї одиниці в кожному рядку. Якщо функціональне відношення задано у вигляді графа, то з кожної вершини, котра зображує першу координату, виходить не більше від однієї дуги.

а) функціональне б) функціональне в) нефункціональне

Рис. 4.4.1. Приклади функціонального і нефункціонального відношень

Нехай – функціональне відношення, . Відповідність від першого до другого елемента кожної пари відношення називається функцією , або відображенням множини D_F в Y.

Графіком функції (відображення) називається сукупність точок виду у декартовому добуткові .

Існує декілька видів відображень, а саме: сюрєктивне, інєктивне, бієктивне.

Функція називається сюр’єктивним відображенням, якщо . На графі, який зображує сюр’єктивне відображення, з будь-якої вершини виходить точно одна дуга, а до будь-якої вершини, що зображує елемент множини , заходить не менше від однієї дуги (рис 4.4.2).

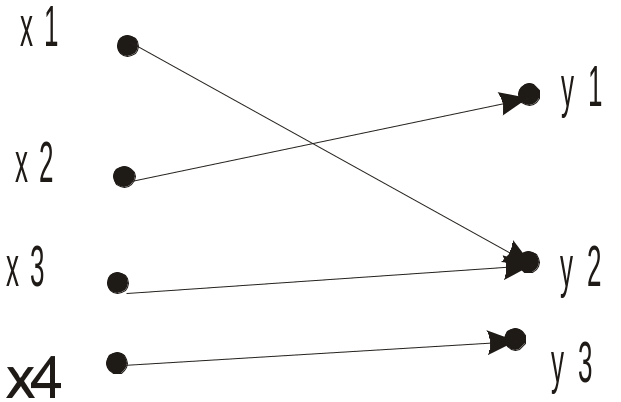
Рис. 4.4.2. Приклад сюр’єктивного відображення

Функція називається ін’єктивним відображенням, якщо з виходить . На графі, що зображує ін’єктивне відображення, з будь-якої вершини виходить точно одна дуга, а до будь-якої вершини, що зображує елемент множини , заходить не більше від однієї дуги (рис 4.4.3).

Рис. 4.4.3. Приклад ін’єктивного відображення

Функція називається бієктивним відображенням, якщо вона сюрєктивна та інєктивна. На графі, котрий зображує бієктивне відображення скінченних множин, із будь-якої вершини виходить точно одна дуга, а до будь-якої вершини, що зображує елемент множини , заходить одна і тільки одна дуга (рис 4.4.4).

Рис. 4.4.4. Приклад бієктивного відображення