2. Бінарні відношення. Способи задавання перерізів
Відношення між елементами двох множин, тобто бінарні відношення, встановлюють відповідність елементів однієї множини X елементам іншої множини Y.
Таке відношення задається деякою сукупністю впорядкованих пар (x,y), які є елементами множини XY. Але це зовсім не означає, що потрібно перелічувати всі такі пари. Часто відношення задається деяким символом, виразом у словесній або символьній формі.
Якщо А – відношення, то відповідність xAy можна записати у вигляді (x,y)A, де АXY.
Елемент x називається першою координатою, а елемент y – другою координатою впорядкованої пари.
Області визначення і значень. Множина перших координат x є областю визначення (лівою областю) Do(A), а множина других координат – областю значень (правою областю) Dз(A) відношення А. Якщо x X і yY, то Do(A)X та Dз(A) Y. У таких випадках говорять, що A є відношенням від X до Y. Його називають також відповідністю і позначають XY. Якщо Y=X, то будь-яке відношення xAy є підмножиною множини XY та називається відношенням у X.
Приклад 1: X={2,3};
Y={3,4,5,6};
XY={(2,3),(2,4),(2,5),(2,6),(3,3),(3,4),(3,5),(3,6)};
відношення “бути подільним” – A={(2,4),(2,6),(3,3),(3,6)};
відношення “=” – B={(3,3)};
відношення “>” – ;
Do(A)={2,3}=X;
Dз(A)= {3,4,6}Y.
Якщо область відношення збігається з деякою множиною X, то говорять, що відношення визначене на X.
Заслуговують уваги три випадки відношень у X:
Повне (універсальне) відношення P= X X, яке має місце для кожної пари (x1, x2) елементів із X. Наприклад, відношення “працювати в одному відділі” на множині відношень співробітників цого відділу.
Тотожне (діагональне) відношення E, рівнозначне x = x, наприклад, рівність на множині дійсних чисел.
Пусте відношення, котре не задовольняє жодна пара елементів із X, наприклад, відношення “бути братом” на множині жінок.
Бінарні відношення можна задати наступними способами:
За допомогою списку, елементами якого є пари, з котрих складається відношення.
2. За допомогою фактор-множини.
Переріз. Розглянемо відношення AXY; якщо xiX, то переріз по xi відношення А, позначений А(xi), є множиною yY таких, що (xi, y ) А.
Множина всіх перерізів відношення А називається фактор-множиною Y по відношенню А і позначається Y/A. Воно повністю визначає відношення А.
Приклад
X={ x1, x2, x3, x4, x5};
Y= { y1, y2, y3, y4};
A= {( x1, y1), (x1, y3), ( x2, y1), ( x2, y3), ( x2, y4), ( x3, y1), ( x3, y2), ( x3, y4), ( x4, y3), ( x5, y2), ( x5, y4)}.
Якщо запишемо під кожним елементом із X відповідний переріз відношення А, то елементи другого рядка утворять фактор-множину Y/A:
x1 x2 x3 x4 x5
{y1,y3} { y1,y3, y4} { y1,y2, y4} {y3} { y2, y4}.
Кінцеве відношення
представляється за допомогою
фактор-множини. Об’єднання перерізів
за елементами деякої підмножини
BX
є
перерізом
A(B)
цієї
підмножини, тобто
A(B)=
Так,
A(x2,
x3)=
A(x2)
A(x3)={
y1,
y2,
y3,
y4}.
3. За допомогою матриць. Цей спосіб – матричний – оснований на представленні відношень за допомогою прямокутної таблиці (матриці). Її стовпці відповідають першим координатам, а рядки – другим координатам. На перетині i-го стовпця та j-го рядка ставиться одиниця, якщо виконується відношення xiAyj і 0, якщо це відношення не виконується. Така матриця містить усю інформацію про відношення А. Наприклад,
|
x1 |
x2 |
x3 |
x4 |
x5 |
y1 |
1 |
1 |
1 |
|
|
y2 |
|
|
1 |
|
1 |
y3 |
1 |
1 |
|
1 |
|
y4 |
|
1 |
1 |
|
1 |
4. За допомогою графів. Вершини графа відповідають елементам множини X та Y, а дуга, направлена з вершини xi до yi , означає, що xiА yi (рис. 4.2.1).
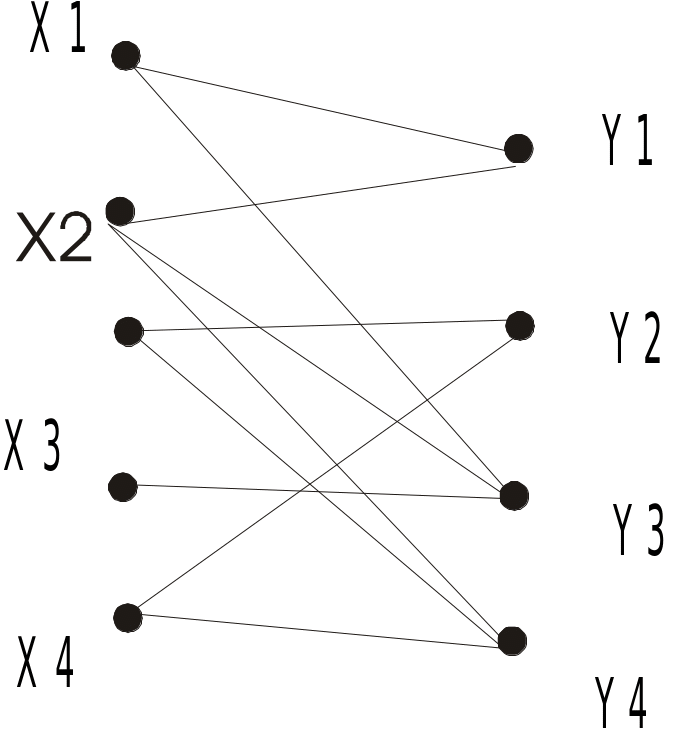
Рис. 4.2.1. Граф відношення від X до Y (біграф)
Приклад: задане відношення (рис. 4.2.2)
А={( x1, x2), (x1, x5), ( x2, x1), ( x2, x3), ( x3, x1), ( x3, x4), ( x4, x3), ( x4, x5), ( x5, x5), ( x6, x2)}.
Рис. 4.2.2. Граф відношень у множині X
Зобразимо графи повного, тотожного та пустого відношення (рис. 5.2.3).
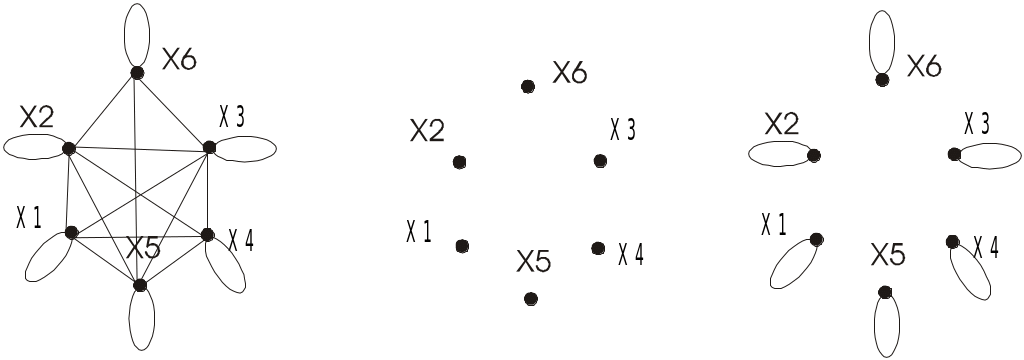
Рис. 4.2.3. Граф повного, пустого й тотожного відношень
Симетричне відношення. Оскільки відношення – це множини, то над ними виконуються всі теоретико-множинні операції. Крім того, для відношення визначаються специфічні для відношення операції: обернення (симетризація) та композиція.
Відношення, симетричне (обернене) деякому відношенню AXY, позначається через А-1 і являє собою підмножину множини Y X, утворену парами ( y, x ) Y X, для якого (x, y ) А. Перехід від А до А-1 здійснюється взаємною перестановкою координат кожної впорядкованої пари, наприклад:
обернене відношення для “ x є дільником y” буде “ y ділиться на x”;
відношення A={(2,4),(2,6),(3,3),(3,6)}, A-1={(4, 2),(6, 2),(3,3),(6, 3)}.
При переході від А до А-1 область визначення стає областю значень і навпаки. Матрицю оберненого відношення одержуємо траснпонуванням вихідної матриці. Граф оберненого відношення знаходимо з вихідного графа заміною направлень усіх дуг на протилежні.
Композиція відношень. Нехай дано три множини X, Y, Z і два відношення AXY та BY Z.
Композицією відношень A й B є відношення С, що складається з усіх тих пар (x,z) X Z для яких існує такий yY, що (x, y ) А та (y,z) B.
Як записати композицію відношень A та B? Якщо виходити із співвідношень xAy і yB z, то xCz=xABz, але для зручності прийнято записувати С=АВ або С=АВ.
Для композиції відношень справедливим є асоціативний закон, тобто D(BA)=(DB)A=DBA. Але не комутативний закон ВААВ, наприклад:
X={ x1, x2, x3, x4, x5};
Y= { y1, y2, y3, y4};
A= {( x1, y1), (x1, y3), ( x2, y1), ( x2, y3), ( x2, y4), ( x3, y1), ( x3, y2), ( x3, y4), ( x4, y3), ( x5, y2), ( x5, y4)};
В= {( y1, z2), ( y2, z1), ( y2, z2), ( y3, z3), ( y1, z2), ( y4, z3)}.
Тоді С={( x1, z2), ( x1, z3), ( x2, z2), ( x2, z3), ( x3, z1), ( x3, z2),( x3, z3), ( x4, z3), ( x5, z1), ( x5, z2), ( x5, z3)}.
Переріз С(x3)={ z1, z2, z3};
B(A(x3))=B({y1, y2, y4})={z1}{ z1, z2}{ z3}={ z1, z2, z3}.
Композиція відношень AXY та BY Z наочно представляється у вигляді графів. Перш за все необхідно до графа відношення А добудувати граф відношення В.
Граф відношення С=ВА одержимо, виключивши вершини, які відповідають елементам множини Y. При виключенні вершини yi кожний шлях, що проходить через неї від вершин x до вершин z, замінюється однією дугою з тим же направленням.
Паралельні гілки з однаковими направленнями відповідають однаковим парам у С і розглядаються як одна гілка (рис. 4.2.4).
Рис. 4.2.4. Побудова графа композиції відношень xAy та yBz
Аналогічно можна одержати матрицю композиції С=ВА як добуток матриць відношень В й А (у порядку їх слідування), яке виконується за звичайним правилом множення прямокутних матриць із наступною заміною відмінного від нуля елемента результуючої матриці. Наприклад:
|
y1 |
y2 |
y3 |
y4 |
|
|
|||||||||||||
z1 |
|
1 |
|
|
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
||||||
z2 |
1 |
1 |
|
|
|
y1 |
1 |
1 |
1 |
|
|
|
|
||||||
z3 |
|
|
1 |
1 |
|
y2 |
|
|
1 |
|
1 |
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
|
|
|
|
* |
y3 |
1 |
1 |
|
1 |
|
= |
z1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
y4 |
|
1 |
1 |
|
1 |
|
z2 |
1 |
1 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z3 |
1 |
2 |
1 |
1 |
1 |
|