5. Маршрути, цикли графів

Нерідко задача на графах потребує виділення різних маршрутів, що мають певні властивості та характеристики. Маршрути довжиною m ребер (не обов’язково різні) таких, що граничні вершини двох сусідніх ребер збігаються (рис 3.2.1).

Приклад

(e₁, e₃, e₂, e₅) – з’єднує v_{1 ,}v₅

(e₅, e₆, e₄, e₄) – з’єднує v_{3 ,}v₅

Замкнутий маршрут приводить у ту ж вершину, з якої він почався.

Маршрут, усі ребра котрого різні, називається ланцюгом, а маршрут, для якого різні всі вершини, називається простим ланцюгом. Замкнутий ланцюг називається циклом, а простий ланцюг – простим циклом, наприклад, (e₂, e₅, e₆) – ланцюг,(e₁, e₂, e₅) – простий ланцюг, (e₂, e₃, e₄, e₅) – цикл, (e₂, e₄, e₅) – простий цикл.

Цикл, який містить усі ребра графа, називається ейлеровим циклом, а граф, що містить такий цикл, називається ейлеровим графом. Простий цикл, котрий проходить через усі вершини графа, називається гамільтоновим.

Маршрут, який не містить дуг, котрі повторюються, називається шляхом, а той, що не містить вершин, які повторюються, – простим шляхом. Замкнений шлях називається контуром, а простий замкнений шлях – простим контуром.

Граф називається циклічним (контурним), якщо він містить хоч один цикл (контур). В іншому випадку він називається ациклічним (безконтурним). Поняття ланцюга та циклу застосовуються до орієнтованих графів. При цьому направлення дуг не враховуються.

Дві вершини графа називаються зв’язними, якщо існує маршрут, котрий з’єднує ці вершини. Граф, будь-яка пара вершин котрого зв’язана, називається зв’язаним графом (рис. 3.5.1).

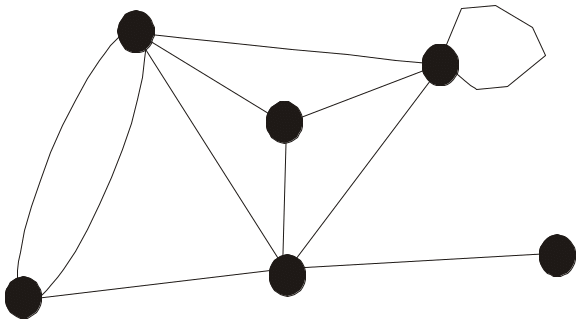
Рис. 3.5.1. Зв’язний граф

Планарність графів. Граф називається плоским, якщо існує ізоморфний йому граф, і він може бути зображений на площині без перетину ребер. На рисунку 3.5.3, хоча ребра графа перетинаються, ізоморфні йому графи не мають перетину ребер.

Два графи (так звані графи Понтрягіна–Куратовського) відіграють фундаментальну роль у теорії планарності.

а) б)

Рис. 3. 5. 2. Графи Понтрягіна–Куратовського: а) повний п’ятикутник, б) дводольний граф

Дводольний граф (рис. 3.5.2, б) є моделлю відомої задачі про три будинки і про три криниці: чи можна від кожної криниці до кожного будинку прокласти дороги так, щоб вони не перетиналися? Планарність є суттєвою властивістю графів, які моделюють комунікаційні зв’язки між об’єктами на площині (дороги між населеними пунктами, водопровідні, газопровідні мережі, лінії передач електроенергії, міжз’єднання на печатних платах електронних приладів і кристалах інтегральних схем). Плоскими графами є різні карти, з якими повязана відома проблема чотирьох фарб: чи можна пофарбувати області, на котрі плоский граф поділяє поверхню, так, щоб ніякі дві суміжні області не були пофарбовані в однаковий колір і щоб при цьому було використано не більше від чотирьох кольорів?

Контрольні запитання

1. Розкрити поняття графа. Застосування графів.

2. Дати поняття орграфа, степінь вершини.

3. Які існують типи графів?

4. Розкрити поняття суміжності, інцидентності графів.

5. Розкрити поняття орграфа ізоморфізму графа.

6. Що являє собою маршрут графа?

7. Що називається планарним графом?

Лекція 4

Аналіз систем на основі поняття відношення. Властивості бінарних відношень. Нечіткі відношення

1. Визначення впорядкованої пари та декартового добутку.

2. Бінарні відношення. Способи задавання перерізів.

3. Властивості бінарних відношень.

4. Функціональні відношення.

5. Нечіткі відношення.

1. Визначення впорядкованої пари та декартового добутку

Багато задач математики, техніки й інших сфер людської діяльності дістають зручну інтерпретацію мовою теорії відношень. Усі арифметичні операції – по суті відношення між числовими множинами. Множина деталей залишається складським майном, доки між ними не реалізуються певні відношення, які перетворюють ці деталі в якийсь механізм або прилад (телевізор, верстат, будинок, міст та ін.).

Відношення застосовують в побудові комп’ютерних баз, які організовані у вигляді таблиць даних, а також застосовуються у програмуванні. Різноманітні відошення складаються між людьми – батьки, діти, начальники, вчителі, учні. Самі дані обробляються і перетворюються за допомогою операцій, математично точно визначених для відношень. Останні реалізують у математичних термінах на абстрактних множинах реальні зв’язки між реальними об’єктами.

Для формального опису всіляких комбінацій з елементів множин, що входять до відношення, використовується поняття декартового добутку множин.

Нехай маємо множини . Декартовим добутком (добутком множин) називається множина всіх упорядкованих наборів з n елементів (що називаються кортежами довжини n), із яких перший елемент належить множині , а другий – множині , n-й – . Декартів добуток , у котрому одна й та ж множина помножується n разів сама на себе, називається декартовим степенем множини і позначається .

Приклад 1

A={a_1,a_2,a_3,a₄}, B={b₁,b₂}, тоді

А  В ={a₁,b₁},{a₁,b₂},{a₂,b₁},{a₂,b₂},{a₃,b₁},{a₃,b₂},{a₄,b₁},{a₄,b₂}.

Приклад 2

A={a_1,a₂}, тоді

A³={(a_1,a₁,a₁),(a_1,a₁,a₂),(a_1,a_2,a₁,),(a_1,a_2,a₂), (a_2,a_1,a₁),(a_2,a_1,a₂),(a_2,a_2,a₁,),(a_2,a_2,a₂)}.

Порядок пар може бути довільним, але розміщення елементів у кожній парі визначається порядком множин, що перемножуються, тому А x В В x А.

N-арне відношення R на множині – це підмножина декартового добутку цих n множин: .

Добуток множин не підлягає асоціативному та комутативному законам, але для нього виконується закон дистрибутивності відносно операцій об’єднання перетину та різниці:

Примітка. У результаті операцій об’єднання, перетину тощо завжди одержуємо множину, елементи котрої (якщо вона не пуста) належать вихідним множинам. Елементи добутку множин суттєво відрізняються від елементів співмножників і являють собою об’єкти іншої категорії.

Нехай N – множина натуральних чисел. Тоді N x N буде множиною пар натуральних чисел (p,q), кожна з котрих визначає найрізноманітніші обєкти: дроби p/q, суми p+q номери будинків і квартир, пари учасників шахового турніру. При цьому (p,q)(q,p).

Якщо n=1, то таке відношення називається унарним, n=2 – бінарним, n=3 – тернарним .