2. Типи скінченних графів

Якщо множина вершин графа скінченна, то він називається скінченним графом. Скінченний граф G=(V, E), що містить p вершин і q ребер, називається (p, q)- графом (рис. 3.2.1).

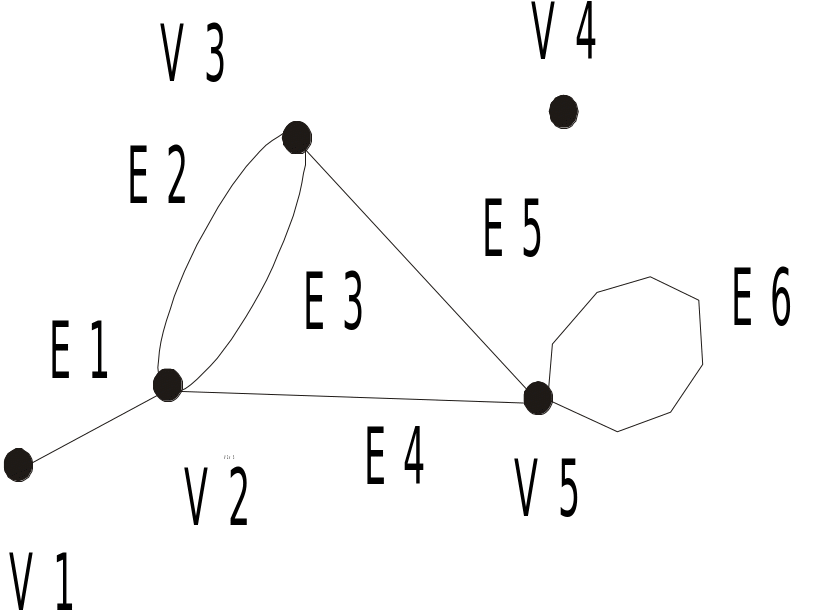
Рис. 3.2.1. Псевдограф (p, q)- графа

Нехай V={v₁, v₂, …v_p} та E={e₁, e₂, …e_q} відповідно множина вершин і ребер. Кожне ребро e_kE й з’єднує пару вершин v_i, v_j  V, є його кінцями (граничними вершинами). Для орієнтованого ребра розрізняють початкову вершину, із якої дуга виходить, та кінцеву вершину, куди дуга заходить. Ребро, граничними вершинами котрого є одна й та сама вершина, називається петлею. Ребра з однаковими граничними вершинами є паралельними і називаються кратними. У загальному випадку граф може містити й ізольовані вершини. Наприклад, для (5, 6) (рис. 3.2.1) графа V={v₁, v₂, v₃, v₄, v₅} E={e₁, e₂, e₃, e_4, e₅, e₆}; e₁, e₃ – паралельні, e₆ – петля, e₄ – ізольована вершина.

Нехай G=(V,E) є не пустий граф. Множину сусідніх вершин v_i у G позначимо як N_G(v_i) чи коротко через N(v_i). Степінь (або валентність) вершини d_G(v_i)=d(v_i) є кількістю |E(v_i)| ребер, що виходять із вершини v_i. За нашим визначенням графа, це рівнозначне кількості сусідніх вершин. Вершина із степенем 0 є ізольованою. Число є мінімальним степенем графа G, а число – максимальним степенем. Якщо всі вершини графа G мають один і той самий степінь k, тоді граф G є k-однорідним або просто однорідним. 3-однорідний граф називається кубічним. Число – середній степінь графа G. Зрозуміло, що . Середній степінь оцінює глобально те, що локально вимірюється степенями вершин – кількості ребер графа G, що припадає на одну вершину. Іноді дуже зручно виражати це відношення як . Величини d і  звичайно тісно взаємопов’язані. Якщо ми підсумуємо степені всіх вершин у графі G, то врахуємо кожне ребро двічі, по одному разу з кожного кінця. Таким чином, , . Тому .

Припущення 1. Кількість вершин непарного степеня у графі є завжди парною.

Припущення 2. Кожний граф G з одним ребром має підграф H, де .

Граф без петель і кратних ребер називається простим, або звичайним. Граф без петель, але з кратними ребрами, називають мультиграфом. Найбільш загальний випадок графа, коли допускаються петлі й кратні ребра, називається псевдографом (рис. 3.2.1). Якщо всі вершини графа ізольовані, тобто V={} та E={}, то він називається пустим.

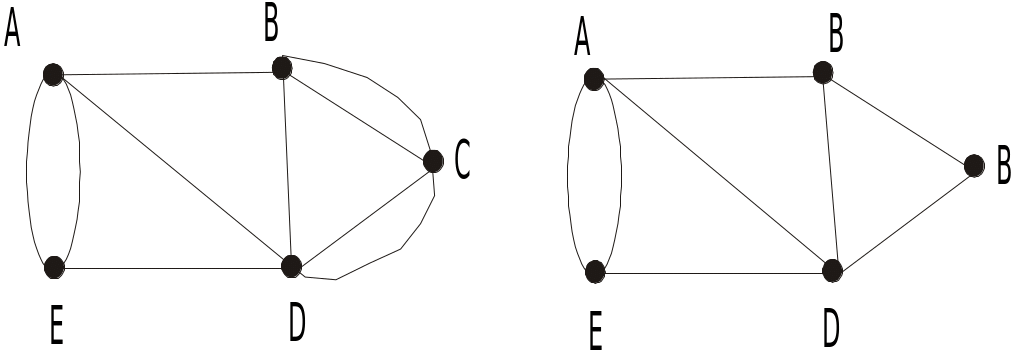
Простий граф, у якого будь-які дві вершини з’єднані ребром, називається повним. Якщо множина вершин V простого графа допускає таке розбиття на дві неперетинані множини V₁ та V₂ (V₁  V₂=), що не існує ребер, які з’єднують вершини однієї й тієї ж підмножини, то вони називаються дводольним, або біграфом (рис. 3.2.2).

а) б)

Рис. 3.2.2. Повний граф (а), дводольний граф (б)

Орієнтований граф називається простим, якщо він не має строго паралельних дуг та петель. Граф, степені всіх вершин якого однакові та рівні r, називається однорідним (регулярним).

3. Орієнтовані графи, зважені графи

Часто зв’язки між об’єктами характеризуються визначеною орієнтацією. Наприклад, на деяких вулицях допускається лише односторонній автомобільний рух, стосунки між людьми визначаються за старшинством. Орієнтовані зв’язки характеризують перехід з одного стану в інший, результати зустрічей між командами у спортивних змаганнях, різні відношення між числами (нерівність, подільність). Для визначення направленого зв’язку між вершинами графа відповідне ребро помічають стрілкою. Якщо ребра з множини Е орієнтовані, то вони називаються дугами, а граф із такими ребрами називається орієнтованим графом (орграфом). Якщо ребра не мають орієнтації, то граф називається неорієнтованим. Дуга позначається парою, тобто початковою і кінцевою вершинами. Ребро {x,y} зазвичай позначають xy (або yx). Якщо пара вершин з’єднується двома чи більшою кількістю дуг, то такі дуги називаються паралельними. При цьому дві дуги, однаково направлені по відношенню до даної вершини, називаються строго паралельними, по-різному направлені – нестрого паралельними. Ясно, що нестрого паралельні дуги, які відображають орієнтацію зв’язку в обох напрямках, по суті рівноцінні неорієнтованому зв’язку і можуть бути замінені ребром. У такому випадкові матимемо змішаний граф, що містить ребра та дуги (рис. 3.3.1).

а) б)

Рис. 3.3.1. Орієнтований (а) граф, змішаний (б) граф

В орієнтованому графі розрізняють додатні d⁺(v_i) і відємні степені вершин d^-(v_i). Очевидно, суми додатних та від’ємних степенів усіх вершин орграфа рівні між собою й дорівнюють кількості всіх дуг.

Зважені графи. Подальше узагальнення відображення зв’язків між об’єктами за допомогою графів полягає у приписуванні ребрам і дугам деяких кількісних значень, якісних або характерних властивостей. У найпростішому випадкові не може бути порядкової нумерації ребер та дуг, що вказує на черговість їх розгляду (пріоритет, ієрархію). Всі ребра й дуги можуть означати довжину (шлях сполучення), пропускну здатність (лінії зв’язку), напруження (електричні ланцюги), валентність зв’язків (хімічні формули), колір провідника (монтаж схем електричного пристрою), характер відношень між людьми (син, брат).

Вагу можна приписувати не лише ребрам і дугам, а й вершинам. Узагалі, вага вершини означає будь-яку характеристику відповідного їй об’єкта (вік людини, атомну вагу елемента, колір предмета). Особливе значення для моделювання фізичних систем набули зважені орієнтовані графи, названі графами потоків сигналів, або сигнальними графами. Вершини сигнального графа ототожнюються з деякими змінними, що характеризують стан системи, а вага кожної вершини означає функцію часу чи деякої величини, що характеризує відповідну змінну (сигнал вершини). Дуги відображають зв’язки між змінними, і вага кожної дуги являє собою числове або функціональне відношення, що характеризує передачу сигналу від однієї вершини до іншої (передача дуги). Сигнальні графи знайшли широке застосування у теорії ланцюгів та систем, а також в інших галузях науки й техніки.