Вопросы к экзамену+ответы(шпоры). Р-РС-ЭП 2 курс, 2 семестр Рябов Н.И. / Ответы / Новая папка / 5

5. Расчёт электрических цепей методом узловых потенциалов.

Режим любой цепи полностью характеризуется уравнениями, составленными на основании первого и второго законов Кирхгофа, причем для определения токов во всех В ветвях необходимо составить и решить систему уравнений с В неизвестными.

Число уравнений, подлежащих решению, можно сократить, если пользоваться методом узловых потенциалов, основанным на применении первого закона Кирхгофа и закона Ома.

Для выяснения сущности этого метода рассмотрим, например, электрическую схему, показанную на рис. 4.16.

Пусть потенциал одного из узлов, например узла 3, принят равным нулю, т. е. ϕ3=0. Такое допущение не изменяет условий задачи, так как ток в каждой ветви зависит не от абсолютных значений потенциалов узлов, к которым присоединена ветвь, а от разности потенциалов между концами ветви.

Запишем уравнения на основании первого закона Кирхгофа для узлов 1 и 2 этой схемы при выбранных положительных направлениях токов

I5 − I4 − I1 + I6 = 0

− I5 − I 6 − I 2 + I3 = 0 (4.28)

Токи в ветвях согласно закону Ома

где ϕ1 и ϕ2 — потенциалы узлов 1 и 2.

После подстановки (4.29) в (4.28) и группировки членов получим

В этих уравнениях, так же как и в уравнениях (4.30), проводимость gpp (с двумя одинаковыми индексами) представляет собой суммарную проводимость ветвей, присоединенных к узлу p, и называется собственной узловой проводимостью этого узла; проводимость gjp=gpj с двумя различными индексами равна сумме проводимостей ветвей, соединяющих между собой рассматриваемые узлы j и p, и называется общей узловой проводимостью этих узлов. Правая часть каждого из уравнений содержит алгебраические суммы произведений ветви ЭДС Epj на проводимость этой ветви g’pj для всех ветвей, присоединенных к узлу p, ток Jp равен алгебраической сумме токов всех источников тока, присоединенных к тому же узлу. В свою очередь, правая часть уравнений (4.33) ток Jp(y) — узловой ток — равен алгебраической сумме — и токов, определяемых источниками ЭДС, которые присоединены к узлу p, при этом следует иметь в виду, что для замкнутых поверхностей сумма всех узловых токов, как это вытекает из первого закона Кирхгофа, равна нулю. К узловым токам можно отнести и уже известные в каких-либо ветвях токи. Проводимости таких ветвей в выражения вида gpp и gjp не входят.

Решив уравнения (4.33), можно определить потенциалы узлов, а зная потенциалы, найти токи во всех ветвях по закону Ома.

Если в цепи имеются ветви с идеальными источниками ЭДС и сопротивлениями этих ветвей можно пренебречь, то при составлении уравнений (4.33) получается неопределенность, поскольку проводимости таких ветвей бесконечно боль шие. Такое затруднение преодолевается путем переноса заданной ЭДС из ветви с нулевым сопротивлени ем через соответствующий узел в другие ветви, присоединенные к тому же узлу и имеющие конечные значения сопротивлений. В результате такого преобразования токи во всех ветвях заданной схемы не изменяются.

Для иллюстрации расс мотрим схему (рис. 4.18, а), у которой сопротивление ветви 2-4 равно нулю, а ЭДС равна Е. Если в каждую в етвь, присоединенную, например, к узлу 2, включить источник напряжения с ЭДС, равной Е и направленно й от узла 2 (на рис. 4.18, а эти ЭДС изображены шт риховой линией), то токи во всех ветвях останутся без изменения, поскольку разности потенциалов между точками 1', 3', 4'будут, так же как и в заданной схеме, равны нулю. Теперь потенциалы узлов 2 и 4, очевидно, одинаковы и их можно объединить в одну точку (рис. 4.18,6). Для полученной схемы с тремя узлами (вм есто четырех) можно составить два независимых уравнения вида (4.33), из которых определяются искомые потенциалы двух узлов, а затем по закону Ома токи во всех ветвях схемы (рис. 4.18,6), после чего легко найти ток в ветви с сопротивлением r=0 (рис. 4.18, а) по первому закону Кирхгофа.

Рассмотренную и анал огичные ей задачи можно решить и без предварительного переноса ЭДС через узел в другие ветви. Действительно, если принять в заданной схеме (рис. 4.18, а) ϕ4=0, то потенциал ϕ2 узла 2, очевидно, будет равен Е. Для определения двух неизвестных потенциа лов ϕ1 и ϕ3 нужно составить уравнения (4.33), которые полностью совпадут с уравнениями, состав ленными для тех же узлов эквивалентной схемы (рис. 4.18,6). Перенос приходится делать, идеальные ЭДС включены в ветви, не имеющие общего узла.

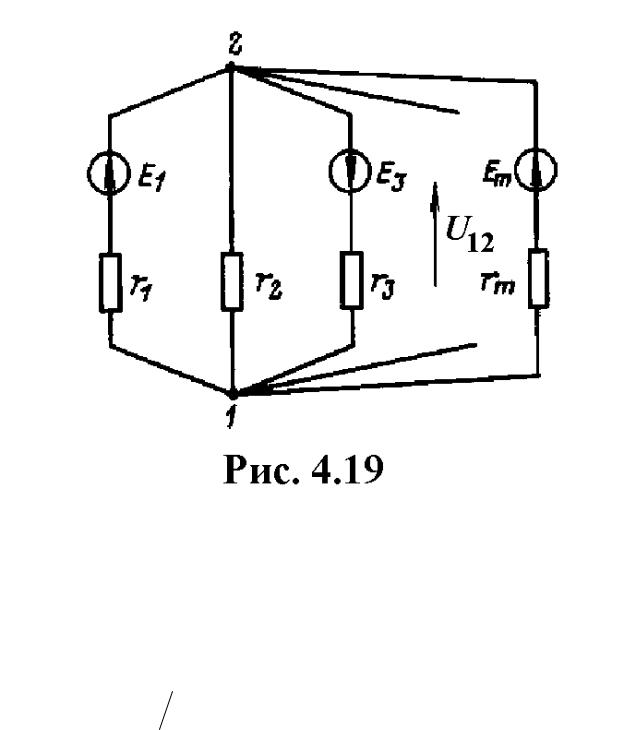
Полезно еще рассмотр еть применение уравнений (4.33) для частного слуучая схемы с двумя узлами и произвольным числом ветвей, все или часть которых содержат источники ЭДС. Требуется определить напряжение между этими узлами.

Пусть между узлами 1 и 2 включено т ветвей (рис. 4.19). Найдем напряжение U12, записав уравнение (4.33) для первого узла

где числитель представляет собой алгебраическую сумму произведений ЭДС на проводимость для всех ветвей, содержащих ЭДС (с положительным знаком записываются ЭДС, направленные к узлу 1), а знаменатель — арифметическую сумму проводимостей всех ветвей, включенных между узлами.

Если между узлами 1 и 2 включены еще источники тока, то их значения следует добавить в числитель (4.34), причем со знаком плюс записываются токи, направленные к узлу 1.

Пример. На рис. 4.20, а изображена электрическая схема с шестью неизвестными токами; ЭДС источников: Е1=6 В, Е2=12 В, Е3=18 В; сопротивления ветвей: r1=r2=r3=2 Ом и r4=r5=r6=6 Ом. Пользуясь методом узловых потенциалов, определить токи во всех ветвях.

Решение. Пусть потенциал точки 0 равен нулю. Запишем уравнения для узлов с потенциалами ϕ1

ϕ2 и ϕ3:

( g1 + g2 + g3 )ϕ1 − g2ϕ2 − g3ϕ3 = −E1 g1 − E2 g2 − E3 g3 , − g2ϕ1 + ( g2 + g5 + g6 )ϕ2 − g5ϕ3 = E2 g2 ,

− g3ϕ1 − g5ϕ2 + ( g3 + g4 + g5 )ϕ32 = E3 g3 ,

или после подстановки численных значений проводимостей и ЭДС

Решив совместно эти уравнения, найдем искомые потенциалы: ϕ1=-9 В; ϕ2=3 В; ϕ3=6 В. Для определения токов в ветвях следует задаться их положительными направлениями. При выбранных положительных направлениях токов ( рис. 4.20)