

1 1. Понятие переменного тока. Мгновенное, амплитудное, действующее значения переменного тока, их взаимосвязь.
Переменным током называют ток, изменяющийся во времени. Значение тока в любой данный момент времени называют мгновенным и
обозначают строчной (малой) буквой i. Для одного из двух возможных направлений тока через поперечное сечение проводника мгновенное значение тока i считают положительным, а для противоположного направления — отрицательным. Направление тока, для которого его мгновенные значения положительны, называют положительным направлением тока. Ток определен, если известна его зависимость от времени i=F(t) и указано положительное направление тока.
Токи, мгновенные значения которых повторяются через равные промежутки времени в той же самой последовательности, называют периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока
i=F(t)=F(t+Т).
Величина, обратная периоду, называется частотой f=1/Т. Частота измеряется в герцах. Частота равна 1 Гц, если период равен 1 с, т. е. 1 Гц=1 с-1.
Постоянный ток можно рассматривать как частный случай периодического тока, период изменения которого бесконечно велик, т. е. частота равна нулю.
Мгновенное значение синусоидального тока определяется выражением
|
2π |
|
|
|
i = I m sin( |
|
t + ψ ) , (6.1) |
|
|
|
|
|
||
|
T |
2π |
||
|
|
|
||
где Im — максимальное значение или амплитуда тока. Аргумент синуса |
|
t + ψ |
||
|
||||
|
|
|
T |
|
называется фазой. Угол ψ равен фазе в начальный момент времени (t=0) и поэтому называется начальной фазой. Фаза с течением времени непрерывно растет. После ее увеличения на 2π весь цикл изменения тока повторяется. Поэтому, когда говорят о фазе для какого-либо момента времени, обычно отбрасывают целое число 2π так, чтобы значение фазы находилось в пределах ±π или в пределах от 0 до 2π. В течение периода Т фаза увеличивается на 2π. Величина 2π/Т показывает скорость изменения фазы и обозначается буквой ω. Принимая во внимание, что f=1/T, можно написать
ω=2π/Т=2πf. (6.2)
Это выражение, связывающее ω и f, послужило основанием называть ω угловой частотой. Измеряется ω числом радианов, на которое увеличивается фаза в секунду. Так, например, при f=50 Гц имеем ω≈314 рад/с. Введя в (6.1) обозначение со для угловой частоты, получим
i=Imsin(ωt+ψ).
Для суждения о периодическом токе вводится понятие о среднем квадратичном значении тока за период, которое называется действующим значением тока, или, короче,
действующим током:
1 T
I = 
 ∫ i 2 dt (6.3)
∫ i 2 dt (6.3)
 T 0
T 0
За один период переменного тока в проводнике с сопротивлением r выделяется тепловая энергия:
T
∫ ri 2 dt
0
1 T
= rT ∫ i 2 dt = rI 2 T T 0
Отсюда следует, что действующий ток численно равен такому постоянному току, при котором за один период в проводнике с тем же сопротивлением выделяется такое же количество тепла, как и при переменном.
Установим связь между действующим значением и амплитудой Im

синусоидального тока:
|
1 |
T |
2 T |
2 |
T |
2 |
||
I 2 = |
∫i 2 dt = |
I m |
∫sin2 (ωt +ψ )dt = |
I m |
∫[1 − cos(2ωt + 2ψ )]dt = |
Im |
||
T |
T |
2T |
2 |
|||||
|
0 |
0 |
0 |
|||||
|
|
|
|
|
||||
Следовательно,
I = Im 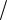

 2 . (6.4)
2 . (6.4)
