Вопросы к экзамену+ответы(шпоры). Р-РС-ЭП 2 курс, 2 семестр Рябов Н.И. / Ответы / 16.0

16. Пассивный двухполюсник на синусоидальном токе. Взаимосвязь комплексного, полного, активного и реактивного сопротивления и проводимости.

ПАССИВНЫЙ ДВУХПОЛЮСНИК

Ток и напряжение на входе любого пассивного двухполюсника (рис. 6.15) связаны законом Ома

U=ZI и I=YI,

где Z и Y — входные комплексные сопротивление и проводимость двухполюсника.

Входному комплексному сопротивлению Z=r+jx соответствует эквивалентная схема двухполюсника, состоящая из последовательного соединения активного сопротивления r и реактивного сопротивления x. Последнее в зависимости от знака следует рассматривать либо как индуктивное, либо как емкостное сопротивление. Поэтому на эквивалентной схеме (рис. 6.16, а) сопротивление x показано условно прямоугольником.

Комплексная проводимость

, (6.34)

откуда

g=r/z²; b=x/z²; (6.35)

и, наоборот,

r=gz²=g/y²; x=bz²=b/y². (6.36)

Из полученных соотношений видно, что b и x всегда имеют одинаковый знак.

Например, для схемы на рис. 6.8 (последовательный RLC контур) получаем для g и b довольно сложные выражения, причем не только b, но и g зависят от частоты:

.

Наоборот, для схемы на рис. 6.12, состоящей из параллельного соединения элементов, получаются простые выражения для проводимостей, но относительно сложные выражения для сопротивлений, причем и эквивалентное активное сопротивление зависит от частоты. По (6.36)

.

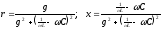Переход от сопротивления Z=r+jx к проводимости Y=g—jb и обратно соответствует замене схемы цепи с последовательным соединением элементов r и jx эквивалентной схемой с параллельным соединением элементов g и —jb и обратно (рис. 6.16, а и б).

Напряжение U можно разложить на составляющие:

U=ZI=(r+jx)I=rI+jxI=U_a+U_p

где U_a=rI — составляющая, совпадающая по фазе с током, называется активной составляющей напряжения; U_p=jxI — составляющая, сдвинутая по фазе относительно тока на угол /2, называется реактивной составляющей напряжения.

Составляющие U_a и U_p можно рассматривать как напряжения на элементах r и x эквивалентной схемы.

На рис. 6.16,в представлена векторная диаграмма двухполюсника при >0, т. е. если x — индуктивное сопротивление. Треугольник, образованный векторами U, U_a и U_p со сторонами, пропорциональными z, r и |x|, называется треугольником напряжений. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны сопротивлениям z, r и |x|, называется треугольником сопротивлений. Из треугольника напряжений следует, что

.

Входной комплексной проводимости Y=g—jb соответствует эквивалентная схема двухполюсника, состоящая из параллельного соединения проводимостей g и —jb. Последняя в зависимости от знака либо индуктивная, либо емкостная. Поэтому на эквивалентной схеме (рис. 6.16,6) проводимость b, показана условно прямоугольником. Ток на входе двухполюсника можно разложить на составляющие :

I=YU=(g—jb)U=gU—jbU=I_a+I_p

где I_a=gU — составляющая, совпадающая по фазе с напряжением, называется активной составляющей тока I_p=—jbU, — составляющая, сдвинутая по фазе относительно напряжения на угол /2, называется реактивной составляющей тока.

Составляющие I_a и I_p можно рассматривать как токи в элементах g и —jb эквивалентной схемы.

Треугольник, образованный векторами I, I_a и I_p, со сторонами, пропорциональными y, g, |b|, называется треугольником токов. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны проводимостям y, g и |b |, называется треугольником проводимостей.

Из треугольника токов имеем

Пример. Цепь состоит из конденсатора емкостью С=10 мкФ и резистора с сопротивлением r=100 Ом, включенных параллельно. Определить, каковы должны быть емкость конденсатора и сопротивление резистора, чтобы при их последовательном соединении получилась цепь, эквивалентная данной при частоте =10³ рад/с.

Решение. Проводимости данной цепи g=1/r=10^-2 См; b=‑b_C=‑С=‑10³1010^‑6=‑10^‑2 См; y²=g²+b²=210^‑4 См².

Сопротивления данной цепи r=g/y²=50 Ом; x=b/y²=‑50 Ом.

Эквивалентная цепь должна иметь такие же сопротивления. Таким образом, искомое сопротивление резистора 50 Ом, а емкость конденсатора С=—1/x=20 мкФ.

Пример. Напряжение и ток на входе пассивного двухполюсника (см. рис. 6.15) u=100sin(314t‑15°) В, i=10sin(314t+45°) А.

Определить параметры двух эквивалентных схем двухполюсника, активные и реактивные составляющие напряжения и тока.

Решение.

U_m=100‑15° В; I_m=1045° А; Z=U_m/I_m=100‑15°/1045°=10‑60°=5‑j53^1/2 Ом;

Y=1/Z=1/(10‑60°)=0,160°=0,05+j0,053^1/2 См;

r=5 Ом; x=‑53^1/2 Ом;

g=0,05 См; b=0,053^1/2 См;

=argZ=_u‑_i=‑15°‑45°=‑60°;

U_am=U_mcos=100соs-60°=50 В;

U_pm=U_m|sin|=100|sin-60°|=503^1/2 В;

I_am=I_mcos=10соs60°=5 А;

U_pm=U_m|sin|=10|sin-60°|=53^1/2 А;

u_a=50sin(314t+45°) В;

u_p=503^1/2sin(314t‑45°) В;

i_a=5sin(314t‑15°) А;

i_p=53^1/2sin(314t+75°) А.