48. Плоская электромагнитная волна в однородном диэлектрике.
Плоская электромагнитная волна в однородном диэлектрике.
В среде нет сторонних токов и зарядов, а векторы напряжённости электрического и магнитного полей зависят только от времени t и одной координаты z, тогда:
Первое уравнение Максвелла и уравнение для напряжённости электрического поля принимают вид:
Из двух последних уравнений
следует, что
не зависит ни от времени, ни от
пространственных координат, следовательно,
.
Второе уравнение Максвелла и уравнение для напряжённости магнитного поля принимают вид:
Из двух последних уравнений
следует, что
не зависти ни от времени, ни от
пространственных координат, следовательно,
.
Тогда система уравнений распадается на две системы:
Системы А и В описывают два
независимых друг от друга поля, в которых
векторы
и
взаимно перпендикулярны.
Рассмотрим систему А:
Продифференцируем первое уравнение по времени, а второе – по координате:
подставляя, получим:
.
Вводя обозначение:
,
получим волновое уравнение:
.
Обозначив:
,
получим:
.
Решением этого уравнения
являются произвольные функции
и
,
т.к.
.
Тогда:
.
Каждое частное решение
и
являются волновыми функциями или
волнами. Рассмотрим
и
.
Если
то:
,
т.е. значения функции
распространяются в положительном
направлении оси z со
скоростью v.
Поверхность, на которой волновая функция в заданный момент времени принимает одинаковые значения, называется волновой функцией, она совпадает с поверхностью равных значений аргумента, или фазы волновой функции.
Уравнение волновой поверхности:
,
это – плоскость z=const,
движущаяся вдоль оси z
в положительном направлении со скоростью
v. Т.е.
- плоская волна. Частное решение
также плоская волна, которая движется
вдоль оси z в отрицательном
направлении со скоростью v.
Аналогично:
.
Подставим Ex и Hy в первое уравнение:
.
Чтобы равенство выполнялось при любых значениях t и z, положим:
откуда:
волновое сопротивление среды:
.
В вакууме диэлектрическая проницаемость равна электрической постоянной ε0:
,
магнитная проницаемость равна магнитной постоянной μ0:
,
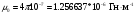скорость распространения волн v равна скорости света:
,
для произвольной среды:
.
Решение уравнения Максвелла представляет собой наложение двух плоских волн, движущихся вдоль оси z в противоположных направлениях, они называются прямой и обратной волнами. Эти волны – поперечного типа: электрический и магнитный векторы лежат в плоскости, перпендикулярной направлению распространения волны.
Рис. 8. Ориентация векторов в плоской волне: а) прямая, б) обратная.
Прямая волна:
,
обратная волна:
,
справедливо соотношение:
Отсюда следует, что и для прямой и для обратной волны количества энергии, запасённой в электрическом и магнитном полях равны друг другу:
.
Вектор Пойнтинга прямой волны направлен по оси z, вектор Пойнтинга обратной волны – в противоположном направлении.
Скорость движения энергии vЭН совпадает со скоростью движения волновой поверхности v. Если прямая волна распространяется в направлении оси z, то за промежуток времени dt через участок S плоскости, перпендикулярной оси z, пройдёт количество энергии dW, равное её величине, заключённой в параллелепипеде длиной vЭНdt и сечением S, т.е.
,
или учитывая предыдущее равенство:
,
с другой стороны, эта величина рассчитывается с помощью вектора Пойнтинга:
,
таким образом:
.
Общее решение системы А является наложением прямой и обратной (падающей и отражённой) волн. В случае бесконечного пространства отражённой волны нет.
Рассмотрим падающую волну, когда электромагнитное поле в точке z=0 меняется во времени по гармоническому закону sint (иногда cost) или в символическом изображении по закону ejωt. Поле в произвольной точке z представляется в виде:
,
или в символическом изображении:
где
.
Зависимость составляющих поля E и H от времени в фиксированной точке z.
Зависимость E и H от z в фиксированный момент времени.
Отсюда видно, что в любой фиксированной точке z составляющие поля имеют не зависящие от z амплитуды Eп и Hп=Eп/Z0 и различные фазы. С увеличением z имеет место отставание фазы на величину kz. Поэтому коэффициент k называют фазовым множителем или коэффициентом фазы. Т.к. величина k=ω/v=2π/λ, где λ - длина волны, определяемая как расстояние, на котором фаза меняется на 2π, то k называется волновым числом. На рисунках показаны: зависимость составляющих поля E и H от времени в фиксированной точке z и зависимость E и H от z в фиксированный момент времени. В последующие моменты времени распределение вдоль оси z будет меняться так, как если бы кривые перемещались вдоль положительного направления оси z со скоростью v. Это – бегущая волна.
Ориентация векторов напряжённости электрического и магнитного полей и вектора Пойнтинга.
Рис. 8. Ориентация векторов в плоской волне: а) прямая, б) обратная.
Зависимость составляющих поля E и H от времени в фиксированной точке z.
Зависимость E и H от z в фиксированный момент времени.