44. Теорема Умова - Пойнтинга о сохранении энергии в электромагнитном поле.
Теорема Умова – Пойнтинга о сохранении энергии в электромагнитном поле.
В произвольном объёме V сосредоточена энергия, равная:
. 101\* MERGEFORMAT (.)
Из первого и второго уравнений Максвелла имеем:
.
Умножая скалярно первое
равенство на
,
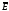а второе на
и складывая, получим:
. 202\* MERGEFORMAT (.)
Из определения векторного произведения следует:
,
учитывая, что:
,
перепишем (1.75) в виде:
,
интегрируя по объёму и меняя знак, получим:
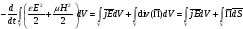303\* MERGEFORMAT (.)
где вектор Пойнтинга:
.
Рис. 23. Взаимная ориентация векторов напряжённости электрического поля, напряжённости магнитного поля и вектора Пойнтинга.
Энергия электромагнитного
поля в каждой точке движется по нормали
к плоскости векторов
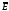и
в сторону поступательного перемещения
правого винта, вращаемого от вектора
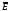к вектору
на наименьший угол. Количество энергии,
протекающей через единичный участок
этой плоскости в единицу времени:
.
Рис. 24. Возможные направления вектора Пойнтинга при убывании энергии в объёме V.
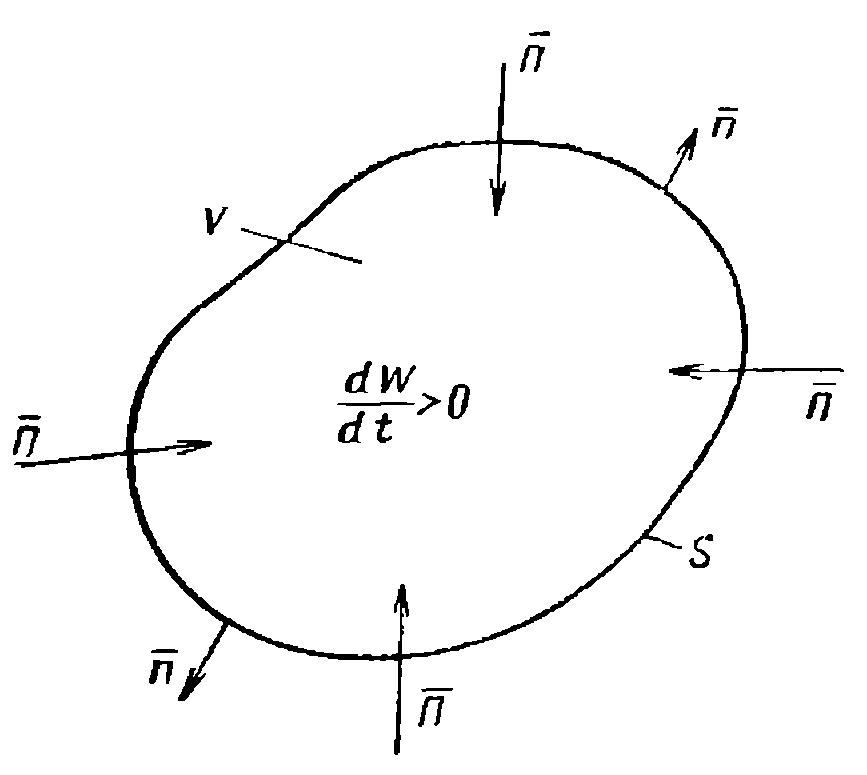
Рис. 25. Возможные направления вектора Пойнтинга при увеличении энергии в объёме V.
В проводнике с током (рис. 25)
вектор напряжённости магнитного поля
к его поверхности, вектор напряжённости
электрического поля
имеет нормальную
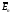и тангенциальную
составляющие, причём последняя направлена
так же, как ток. Поэтому вектор Пойнтинга
у поверхности имеет вид:
.
Первое слагаемое вектора
Пойнтинга
направлено вдоль проводника и определяет
энергию переносимую вдоль проводника.
Второе слагаемое
направлено вглубь проводника, на
постоянном токе это энергия, переходящая
в тепло. Т.о. энергия, переносимая вдоль
проводника определяется нормальной
составляющей вектора напряжённости
электрического поля
,
а энергия, входящая в проводник (потери)
определяется тангенциальной составляющей.
Рис. 26. Поле на поверхности проводника с током.
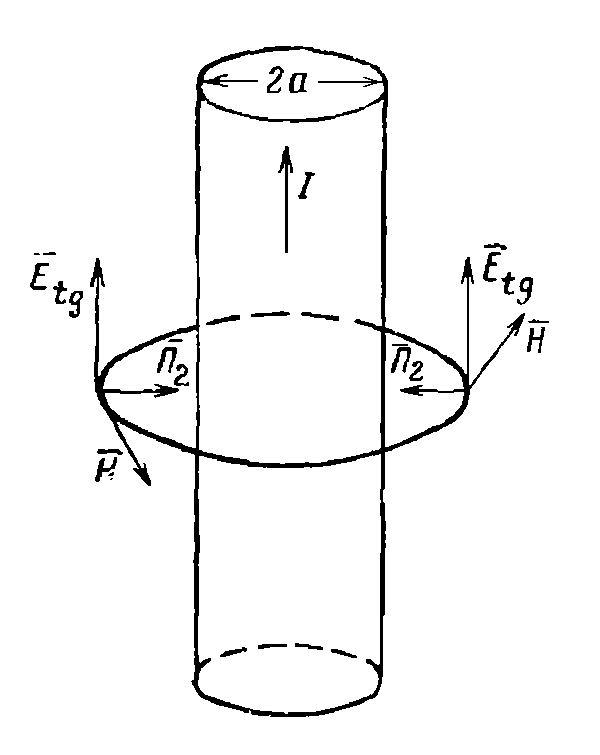
Рис. 27. Движение энергии внутри проводника с током.
Рассчитаем поток энергии,
входящей в проводник на участке длиной
l. Проводник имеет
форму цилиндра с радиусом a
и по нему течёт ток I.
На рис. 27. показано направление векторов
у поверхности проводника. Т.к.
и
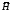перпендикулярны друг к другу, касательны
к поверхности проводника и одинаковы
во всех точках проводящей поверхности,
то поток мощности внутрь проводника
равен:
,
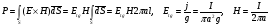где: S - поверхность проводника, j - плотность тока в проводнике. Тогда:
.
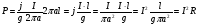Поток электромагнитной энергии равен количеству тепла, выделенному по закону Джоуля – Ленца.
Передача энергии вдоль линии
постоянного тока. На рис. 28 а) схема
линии, на рис. 28 б) силовые линии поля в
поперечном сечении. Если сопротивление
линии равно нулю, у поверхности проводов
вектор напряжённости электрического
поля имеет только нормальную составляющую.
У потребителя R основной
составляющей напряжённости электрического
поля является тангенциальная. Направление
векторов
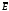и
вблизи верхнего и нижнего проводов
таково, что в обоих случаях вектор
Пойнтинга направлен от источника к
потребителю.
Рис. 28. Движение энергии вдоль линии постоянного тока.
а) схема линии, б) силовые линии поля в поперечном сечении.
Энергия течёт к нагрузке в диэлектрике, окружающей провода, энергия вошедшая в провод (если его сопротивление ненулевое), целиком превращается в тепло. Т.о. провода являются направляющими для передачи энергии в диэлектрике.