Task 4. Investigation of resonance phenomena in an electrical circuit

Objective:

1. Experimental determination of the effect of frequency sinusoidal voltage to the re-presses of the series and parallel circuits, RLS, conditions of ground-loop resonance and the construction of the resonance curves.

2. Consolidate skills simulation in Matlab.

Task will be executed in two phases - in section A study sequential RLS-chain, in section B - circuit with parallel inductance and capacitance.

To successfully conduct research to learn the content of the job, exposition a theoretical introduction, and the rules of the assembly of electrical circuits in Matlab.

Задание 4. Исследование резонансных явлений в электрической цепи

Цель исследования:

1. Экспериментальное определение влияния частоты синусоидального напряжения на режимы работы последовательной и параллельной RLС-цепей, определение условий возникновения резонанса и построение резонансных кривых.

2. Закрепление навыков моделирования в Matlab.

Задание выполняется в два этапа – в разделе А исследуется последовательная RLС-цепь, в разделе Б – цепь с параллельным включением индуктивности и ёмкости.

Для успешного проведения исследований необходимо усвоить содержание задания, изложенное в теоретическом введении, и правила сборки электрических схем в Matlab.

Section A. The study of resonance phenomena in an electrical circuit

with series inductance and capacitance

1A. Theoretical introduction

In this study the resonance phenomena in electrical circuits are considered sisinusoidal current, containing a resistor R, inductance L and capacitor C (RLC-circuit). In this regard, we consider some concepts and definitions.

Characteristics of sinusoidal

Instantaneous value of the sinusoidal current is given by the following form (see waveforms of task 3): _(4.1)

Раздел А. Исследование резонансных явлений в электрической цепи

с последовательным включением индуктивности и емкости

1А. Теоретическое введение

В данном исследовании резонансные явления рассматриваются в электрических цепях синусоидального тока, содержащих резистор R, индуктивность L и конденсатор C (RLC-цепи). В связи с этим рассмотрим некоторые понятия и определения.

Характеристики синусоидального тока

Мгновенное значение синусоидального тока определяется выражением следующего вида (см. осциллограммы задания 3):

(4.1)

Wherе - maximum value or amplitude of current.Argument of sin determines stage or phase of the harmonic current variation and thus is called phase angle, or just a phase.The value represents the value of phase angle at the initial time and so called the initial phase angle, shorter than the initial phase. Phase angle with time is continuously increasing. After increasing the phase angle on or any multiple of the cycle of current variation is repeated. During the period of time equal to one period T, phase angle is changed to . The value measures the rate of change of phase angle and is denoted by the letter _{Taking into account that the frequency of the sinusoidal voltage we can write:}

_{( 4.2)}

где – максимальное значение или амплитуда тока. Аргумент синуса определяет стадию или фазу гармонического изменения тока и поэтому называется фазным углом или просто фазой. Величина представляет значение фазного угла в начальный момент времени ( ) и поэтому называется начальным фазным углом, короче начальной фазой. Фазный угол с течением времени непрерывно возрастает. После увеличения фазного угла на или на любое кратное весь цикл изменения тока повторяется. За промежуток времени, равный одному периоду Т, фазный угол меняется на . Величина измеряет скорость изменения фазного угла и обозначается буквой Принимая во внимание, что частота синусоидального напряжения , можно записать

. (4.2)

This expression, which connects and , served as the basis for the name value of the angular frequency.It is measured with a number of radians, on which the phase angle is changed per second.For example at

we have

Introducing the notation

for angular frequency, expression will write as: (4.3)

Это выражение, связывающее и , послужило основанием для наименования величины угловой частотой. Измеряется радианов, на которое меняется фазный угол за секунду. Так, например, при имеем Вводя обозначение для угловой частоты, выражение (4.1) запишем в виде

(4.3)

Obtained in the job two analytical expressions for the capacitive and inductive in resistance in the light of this concept of angular frequency ω written respectively as: and _{These resistance were called reactance, in contrast to resistance R.}

_{Effective value of alternating current. From experiments and practice it is known that the mechanical force of interaction of two conductors, which runs the same current that is proportional to the instantaneous current. The thermal effect of the current and proportional to the square of current. To assess the effect of alternating current is introduced mean square critical value for the current period T, which is called active (or effective) value AC.}

Полученные в задании 2 аналитические выражения для ёмкостного и индуктивного сопротивлений с учётом введенного понятия угловой частоты запишутся соответственно в виде: and Эти сопротивления получили название реактивных сопротивлений в отличие от активного сопротивления R.

Действующее значение переменного тока. Из экспериментов и практики известно, что механическая сила взаимодейсивия двух проводников, по которым протекает один и тот же ток, пропорциональна квадрату мгновенного значения тока. Тепловое действие тока также пропорционально квадрату тока. Для суждения о действии переменного тока вводится среднее квадратическое значение тока за период Т, которое называется действующим (или эффективным) значением переменного тока.

Relationship between the current value I and the amplitude I_m of sinusoidal current Im is determined by ; similar dependence connects and voltage .

Resonance in the unbranched chain

Resonance of such mode is called an electric circuit containing a resistor, capacitor and inductor, which Х_С = Х_L or Due to Х_С = Х_{L opposite phase voltage at the inductance and capacitance are equal in value (see waveforms of task 3), so the resonance in the unbranched chain, ie in series connection R, L and C is called a resonance voltage.}

Связь между действующим значением I и амплитудой I_m синусоидального тока опреде-ляется соотношением ; аналогичная зависимость связывает и напряжения .

Резонанс в неразветвлённой цепи

Резонансом называется такой режим электрической цепи, содержащей резистор, кон-денсатор и катушку индуктивности, при котором Х_С = Х_L or При Х_С = Х_L противоположные по фазе напряжения на индуктивности и ёмкости равны по величине (см. осциллограммы задания 3), поэтому резонанс в неразветвлённой цепи, т.е. при последовательное соединение R, L и C получил название резонанса напряжений.

From the expression followthat resonance can be achieved by changing either the frequency of the applied voltage or circuit parameters - the capacity or inductance.

For given parameters L and C frequency change alters the circuit reactance . Change reactance leads to changes in the chain. In the resonance mode inductive and capacitive reactance . (4.4)

The value is called characteristic impedance of the circuit or circuit.

Angular frequency at which resonance occurs is called resonance angular frequency

At resonance the voltage across the inductance and capacitance can greatly exceed the applied voltage to the circuit.

Из условия следует, что резонанса можно достичь, изменяя либо частоту приложенного напряжения, либо параметры цепи – ёмкость или индуктивность.

При заданных параметрах L и C изменение частоты приводит к изменению реактивного сопротивления цепи . Изменение реактивного сопротивления приводит к изменению режима цепи. В режиме резонанса индуктивное и ёмкостное сопротивления

. (4.4)

Величина называется характеристическим сопротивлением цепи или контура.

Угловая частота, при которой наступает резонанс, называется резонансной угловой частотой

При резонансе напряжения на индуктивности и ёмкости могут значительно превышать приложенное к цепи напряжение.

Thus, the resonance mode:

1. Reactance circuit is zero(X = Х_L – Х_C = 0);

2. Current in the circuit reaches its maximum 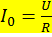- is the current value of the current at resonance;

3. 3. The voltage on the active resistance R equal to the voltage source U.

The ratio of voltage to the inductance or capacitance to voltage applied to the circuit at resonance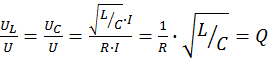 (4.5)

called the coefficient of resonance or Q factor circuit. Coefficient of resonance points, how many times the voltage across the inductance or capacitance is greater than the voltage applied to the circuit. It is obvious that , if Dependence of the current in the circuit from the frequency change made ​​to represent the boundary graphically so-called resonance curve. Resonance curves of successive RLC-circuits are constructed from the results of simulation modes for variations of the frequency of the source sys-sinusoidal voltage.

Таким образом, в режиме резонанса:

1. Реактивное сопротивление цепи равно нулю (X = Х_L – Х_C = 0);

2. Ток в цепи достигает максимального значения – это действующее значение тока при резонансе;

3. Напряжение на активном сопротивлении R равно напряжению источника U.

Отношение напряжения на индуктивности или ёмкости к напряжению, приложенному к цепи, при резонансе

(4.5)

называют коэффициентом резонанса или добротностью контура.

Коэффициент резонанса указывает, во сколько раз напряжение на индуктивности или на ёмкости больше, чем напряжение, приложенное к цепи. Очевидно, что , если

Зависимость тока в исследуемой цепи от изменения частоты принято представлять графически так называемой резонансной кривой. Резонансные кривые последовательной RLC-цепи строятся по результатам моделирования режимов при вариациях частоты источника синусоидального напряжения.

2A. Assembling the principal electric circuit diagrams

Load the Simulink Library Browser (toolbar button MATLAB). Create a new model (File à New à Model). To simulate our scheme we use SymPowerSystem.

As the circuit elements using a combination of Series RLC Branch (connected in series resistance, inductance and capacitance) of the Library Elements (Fig. 4.1).