Тема в. Исследование зависимости остаточного ресурса системы авионики
от продолжительности безотказной работы и заданного уровня безотказности
(радиоэлектронное оборудование – варианты 25 – 36)
1B. Theoretical introduction
Under the remaining life of the system after some operating time t, if the system to this point has kept a usable state, understand its running time, since the instant t, to move it inoperable at the established modes of application of (flight conditions).
Information about the residual operating time can better ensure the sequel operation of avionics.
Considered in a modular control system of electronic display (EIS) consists of elements and components of electronic equipment. When calculating the reliability of systems in which failures are predominant electronic components (ICs, transistors, capacitors, etc.), as a theoretical model of reliability using the Xia-DN-distribution. Consequently, for programming the calculations of the residual system resources will be used by electronic display nonmonotonic diffusion (DN) distribution.
To quantify the residual life of products and avionics systems apply the following two indicators
1В. Теоретическое введение
Под остаточным ресурсом системы после некоторой наработки t, если система к этому моменту сохранила работоспособное состояние, понимают её наработку, начиная с момента t, до перехода её в неработоспособное состояние при установленных режимах применения (режимах полёта).
Информация об остаточной наработке позволяет более эффективно обеспечивать дальнейшую эксплуатацию авионики.
Рассматриваемая в модульной контрольной работе Система Электронной Индикации (СЭИ) состоит из элементов и компонентов электронной техники. При расчётах надёжности систем, у которых преобладающими являются отказы электронных элементов (микросхемы, транзисторы, конденсаторы и т.п.), в качестве теоретической модели надёжности используется DN-распределение. Следовательно, для программирования вычислений остаточных ресурсов системы электронной индикации будет использоваться диффузионное немонотонное (DN) распределение.
Для количественной оценки остаточного ресурса изделий и систем авионики применяют следующие два показателя:
The average residual life of r(t), defined as the expectation of remaining life after the operating time t. Средний1 остаточный ресурс r(t), определяемый как математическое ожидание остаточного ресурса после наработки t. |
Dependence for estimating the mean residual life in general has the form:
(5.4)
where t - uptime of the system from the beginning (t = 0) of its operation, flight hours;
R(t) - probability of system uptime with an operating time of t;
f(t) - density of use to failure in the operation of the system.
Зависимость для оценки среднего остаточного ресурса в общем случае имеет вид:
(5.4)
где t – продолжительность безотказной работы системы от начала (t = 0) её эксплуатации, лётных часов;
R(t) – вероятность безотказной работы системы при наработке t;
f(t) – плотность распределения наработки до отказа при эксплуатации системы.
Gamma-percent residual resource rg(t), defined as operating time, starting from some instant t, during which the product worked flawlessly will be conditional state probability level g. Гамма-процентный остаточный ресурс rg(t), определяемый как наработка, начиная с некоторого момента t, в течение которой безотказно проработавшее изделие будет иметь условную вероятность безотказной работы уровня g. |
Analytical expression for the gamma-percent residual resource rg (t) in general form is written in accordance with the above-stated definition of this indicator longevity sequence:
(5.5)
where g – specified level of reliability - the probability of failure-free operation, expressed as a percentage;
– state
probability of the interval of use rg(t),,
calculated from the condition that within time t
the
system was operational;
Аналитическое выражение для гамма-процентного остаточного ресурса rg(t) в общем виде запишется в соответствии со сформулированным выше определением этого показателя долговечности:
(5.5)
где g – заданный уровень безотказности – вероятность безотказной работы, выраженная в процентах;
– вероятность безотказной работы системы на интервале наработки rg(t), вычисленная при условии, что в течение времени t система была работоспособной;
–
state
probability at an operating time t plus the gamma-percent residual
resource rg(t)
In
DN-reliability model state probability for any value t of use is
determined by the dependence of the form:
(5.6)
– вероятность безотказной работы при наработке t плюс гамма-процентный остаточный ресурс rg(t).
В DN-модели надёжности вероятность безотказной работы при любом значении наработки t определяется зависимостью вида:
(5.6)
where F (×) - the normal function of the normalized distribution of the argument in parentheses.
Shows the calculated values to estimate the residual resource r(t) and rg(t)avionics system, taking into account the accepted model of reliability.
Expression for calculating the expectation of the residual life of r(t) has the following form:
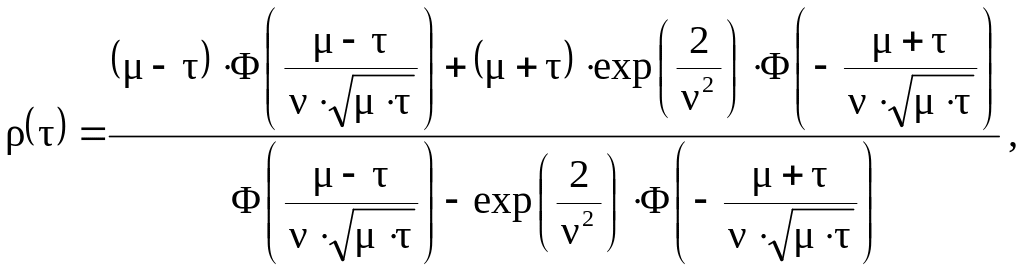(5.7)
where m – mean time to system failure (fail-safe feature of the system), flight hours;
n - the coefficient of variation (range) operating time to failure of the system relative to the mean m.
где Ф(×) – функция нормального нормированного распределения от аргумента в круглых скобках.
Приведём расчётные зависимости для оценки значений остаточных ресурсов r(t) и rg(t) системы авионики с учётом принятой модели надёжности.
Выражение для расчёта математического ожидания остаточного ресурса r(t) имеет следующий вид:
(5.7)
где m – средняя наработка системы до отказа (характеристика безотказности системы), лётных часов;
n – коэффициент вариации (разброс) наработки системы до отказа относительно среднего значения m.
2B. Algorithm for estimating the gamma-percent residual life of EIS
The expression for the gamma-percent residual resource rg(t)is obtained from (5.4), which is written as
(5.8)
substituting the corresponding expressions for R (t) (5.8) becomes:
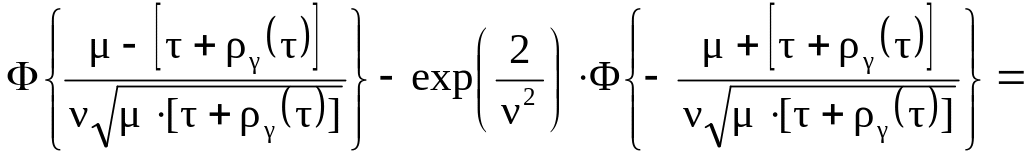
(5.9)
The
right-hand side of (5.9) is defined as the numerical values of
m, ν, t and g are known (given) and denote it
(5.10)
In the left-hand side of (5.9) the argument of the normalized normal distribution expressed in terms of dimensionless operating time:
.
(5.11)
Expression (7) is, thus, to the form (5.12)
(5.12)
with one unknown x, which depends on two parameters - X (g1, n). (5.12) with respect to X - transcendental, since the required X explicitly from the equation is not expressed, a solution is possible by numerical methods.
Then for a known value of the dimensionless (reduced) the estimated operating time X dependence for estimating the gamma-percent residual life of the product we get from (5.11):
Consistent implementation of the decisions described here determines the dependency algorithm for prediction of gamma-percent residual life of electronic display