2.Приток жидкости к скважине , расположенной вблизи непроницаемой границы.

Такая задача может возникнуть при расположении добывающей скважины возле сброса или границы выклинивания продуктивного пласта .

В этом случае реальную скважину-сток зеркально отображают относительно непроницаемой границы фиктивной скважиной-стоком . Решение аналогично предыдущему случаю. В данном случае скорость фильтрации на непроницаемой границе направлена вдоль границы , т.е. граница является линией тока и фильтрация через неё отсутствует.

. (9)

; ;

. (10)

. (11)

; . (12)

. (13)

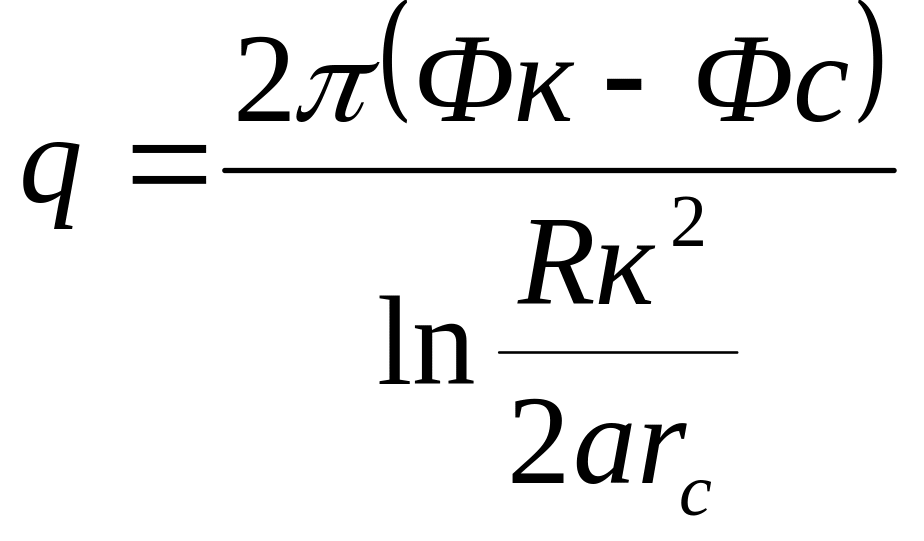. (14)

3. Приток жидкости к скважине , эксцентрично расположенной в круговом пласте.

Пусть в плоском пласте постоянной толщины h с круговым контуром питания радиуса Rк , на котором поддерживается постоянный потенциал Фк, эксцентрично расположена скважина-сток А, на которой поддерживается постоянный потенциал Фс . Требуется определить дебит скважины и потенциал в любой точке пласта .

Отобразим скважину-сток А фиктивной скважиной-источником А’ , расположенной на расстоянии а от скважины А. Расстояние а определим из условия постоянства потенциала на окружности контура питания (в точках и ).

.

(15)

. (16)

Из (15) и (16) :

. (17)

Откуда

(18)

Для того чтобы определить дебит скважины А , запишем выражение потенциала на её забое :

. (19)

Вычитая (19) из (15) , получим :

. (20)

Подставляя (16) в (20) , получим :

(21)

Из (21) дебит скважины :

. (22)

При эксцентриситете формула (22) обращается в формулу Дюпюи.

Потенциал в любой точке пласта М :

. (23)

Вычитая из (23) (19) и учитывая (16) , получим :

. (24)