
- •Курс лекций
- •Подземная гидромеханика
- •I. Основные понятия и законы фильтрации
- •1.Фильтрационные характеристики пористых сред.
- •Кривая распределения пор по диаметрам
- •2. Закон фильтрации Дарси.
- •3. Закономерности неламинарной фильтрации.
- •4. Особенности фильтрации при малых скоростях.
- •II. Дифференциальные уравнения фильтрации флюидов в нефтегазоносных пластах
- •1. Уравнение неразрывности.
- •2. Дифференциальное уравнение движения.
- •3. Уравнения состояния флюида и пористой среды.
- •4. Режимы нефтегазоводоносных пластов.
- •III. Установившееся движение несжимаемой жидкости в пористой среде
- •Дифференциальное уравнение установившейся
- •2. Прямолинейно-параллельный фильтрационный поток.
- •3. Плоскорадиальный фильтрационный поток.
- •4. Радиально-сферический фильтрационный поток.
- •IV. Фильтрационные течения несжимаемой жидкости в неоднородных пластах
- •1. Прямолинейно-параллельный фильтрационный поток в слоисто-неоднородном пласте.
- •Прямолинейно-параллельный фильтрационный поток в
- •3. Плоскорадиальный фильтрационный поток в зонально-неоднородном пласте.
- •V. Одномерные фильтрационные потоки при нелинейных законах фильтрации
- •1. Прямолинейно-параллельный фильтрационный поток.
- •2. Плоскорадиальный фильтрационный поток.
- •VI. Установившаяся плоская фильтрация
- •1. Точечные стоки и источники.
- •2. Метод суперпозиции.
- •III. Приток жидкости к группе скважин в пласте
- •VII. Метод отображения источников и стоков
- •1.Приток жидкости к скважине в пласте с прямолинейным контуром питания.
- •2.Приток жидкости к скважине , расположенной вблизи непроницаемой границы.
- •3. Приток жидкости к скважине , эксцентрично расположенной в круговом пласте.
- •VIII. Гидродинамика несовершенных скважин
- •2. Установившаяся фильтрация упругой жидкости.
- •3. Прямолинейно-параллельный фильтрационный поток идеального газа.
- •4. Плоскорадиальный фильтрационный поток
- •5. Плоскорадиальный фильтрационный поток реального газа по закону Дарси.
- •X. Неустановившееся движение упругой жидкости
- •1. Упругий режим пласта и его характерные особенности.
- •2.Упругий запас жидкости в пласте.
- •3.Дифференциальное уравнение неустановившейся
- •4.Плоскорадиальный фильтрационный поток упругой
- •5. Интерференция скважин в условиях упругого режима.
- •6. Приближенные методы решений.
- •XI. Взаимное вытеснение несмешивающихся жидкостей.
- •Прямолинейно – параллельное вытеснение нефти водой.
- •2.Плоскорадиальное вытеснение нефти водой.
- •3.Конус подошвенной воды.
- •XII. Фильтрация многофазных систем.
- •1 .Характеристики многофазной фильтрации.
- •2. Дифференциальные уравнения многофазной фильтрации.
- •3. Одномерная фильтрация двухфазной жидкости.
- •XIII. Движение жидкостей в трещиноватых
- •1. Особенности фильтрации в трещиноватых
- •2.Уравнение неразрывности потока в трещиноватых
- •4. Установившаяся одномерная фильтрация
- •XIV. Фильтрация неньютоновских жидкостей
- •Законы фильтрации неньютоновских жидкостей.
- •Одномерная фильтрация вязкопластичной жидкости.
- •I. Основные понятия и законы фильтрации . . . . . . . . 3
- •1. Фильтрационные характеристики пористых сред. . . . . . . . 3
- •2. Закон фильтрации Дарси. . . . . . . . . . . . . . . . . . . . . 5
- •5. Интерференция скважин в условиях упругого режима. . . . 60
- •2. Дифференциальные уравнения многофазной фильтрации . . .72
- •1. Особенности фильтрации в трещиноватых
3. Плоскорадиальный фильтрационный поток в зонально-неоднородном пласте.
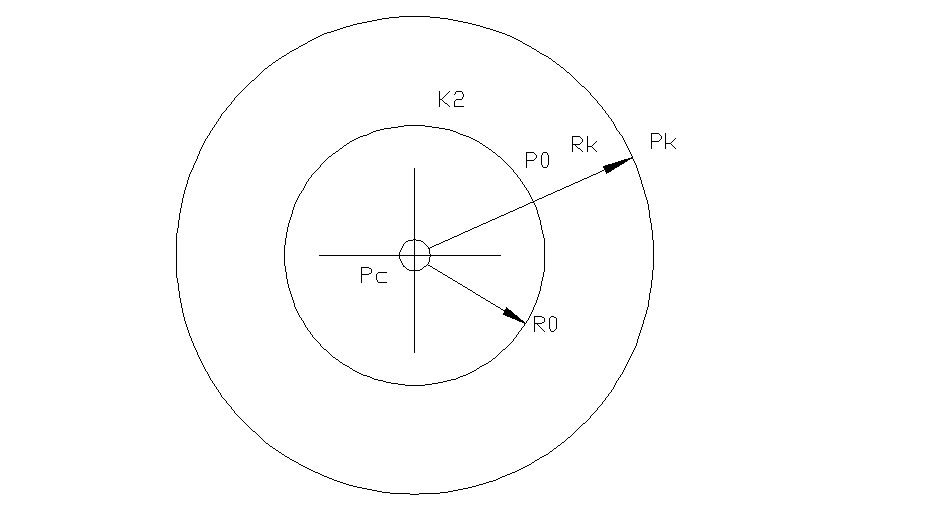
Если при плоскорадиальном притоке жидкости к гидродинамически совершенной скважине по закону Дарси зоны разной проницаемости имеют кольцеобразную форму, то формула дебита скважины для двухзонального пласта имеет вид :
Q
=
 . (12)
. (12)
Распределение давления по зонам:
 ;
;
![]()
![]() (13)
(13)
 ;
;
![]() . (14)
. (14)
Возможен
случай, когда проницательность пласта
в призабойной зоне является функцией
:
![]() --- возрастает
или уменьшается от
--- возрастает
или уменьшается от
![]() -на забое скважины до
-на забое скважины до
![]() на
границе призабойной зоны
на
границе призабойной зоны
![]() .
. ![]()
![]() .
.
Если в призабойной зоне проницаемость изменяются линейно:
![]() ,
(15)
,
(15)
![]() ,
,
![]() ,
,
то дебит скважины можно определить по формуле:
 .
(16)
.
(16)
V. Одномерные фильтрационные потоки при нелинейных законах фильтрации
1. Прямолинейно-параллельный фильтрационный поток.
Рассмотрим прямолинейно-параллельный фильтрационный поток, фильтрация которого подчиняется нелинейному степенному закону
![]() (
(
![]() )
, (1)
)
, (1)
где С и n – известные опытные константы.
Степенной нелинейный закон (1) описывает турбулентные режимы фильтрации.
![]()
. (2) Из (1) и (2) получаем:
![]() .
(3)
.
(3)
 .
(4)
.
(4)

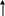
 Р
Р![]()
 Р
Р

Р![]()






 h
Х
h
Х
0 х
Из (4) дебит потока:
Q=
c(![]() .
(5)
.
(5)
Проинтегрируем (3) следующим образом:
 .
(6)
.
(6)
![]() .
(7)
.
(7)
Подставив в (7) Q из (5) получим:
. (8)
Таким образом распределение давления при нелинейном законе фильтрации линейно и в точности совпадает с распределением давления в аналогичном потоке при фильтрации по линейному закону Дарси.
2. Плоскорадиальный фильтрационный поток.
Рассмотрим плоскорадиальный фильтрационный поток несжимаемой жидкости, фильтрация которого подчиняется квадратичному закону Краснопольского:
![]() .
(9)
.
(9)
Обозначим
![]() и запишем (9) в дифференциальной форме:
и запишем (9) в дифференциальной форме:
![]() .
(10)
.
(10)
Из
(10) …..
![]() . (11)
. (11)
Интегрируем
(11)…
 ; (12)
; (12)
![]() ,
(13)
,
(13)
откуда:
 .
(14)
.
(14)
Так
как
![]() <<
<<![]() ,
то (14) можно записать в виде:
,
то (14) можно записать в виде:
![]() .
(15)
.
(15)
Проинтегрируем (11) следующим образом:
 .
(16)
.
(16)
Используя (14), получим распределение давления в пласте:
 .
(17)
.
(17)
Т.о. в данном случае распределение давления имеет тот же вид, что и для линейного закона Дарси, но для радиально-сферического фильтрационного потока.
