Файловый архив студентов. Файловый архив студентов.
1302 вуза, 5134 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Московский государственный институт электроники и математики (технический университет)
Предмет:
Электротехника
Файл:

Домашние работы по Электротехнике / Mine_var2

.doc
Скачиваний:
19
Добавлен:
20.05.2014
Размер:
544.26 Кб
Скачать
☆

Министерство Образования

Российской Федерации

Московский Государственный Институт

Электроники и Математики

(Технический Университет)

Кафедра "Вычислительные системы и сети"

Домашняя работа

по дисциплине “ Электротехника ”

на тему

“ Переходные процессы в линейных электрических цепях ”

Выполнил: Мурашёв И.А

Группа ЭП-41

Проверил: Артамонов А. Т.

Вариант 16

Москва 2003

Задание:

В момент времени t=0 коммутирует рубильник 1, а через промежуток времени t1-рубильник 2 (t1 принять равным постоянной времени первоначального переходного процесса).

Требуется определить:

  1. Выражение для токов i1(t) и i2(t) классичечким методом;

  2. Ток i2(t) операторным методом;

  3. Практическую длительность второго переходного процесса, а в случае колебательного характера этого процесса также и период свободных колебаний и логарифмический декремент колебаний;

  4. Построить график i1(t) для обоих переходных процессов, причем оба переходных процесса должны быть расположены один за другим по оси времени.

Выполнение:

  1. Найдем выражение для токов i1(t) и i2(t) классичечким методом.

П ри замыкании рубильника 1 начнется первый переходный процесс. Найдем ток i1 в этом случае (i2 равен 0, т.к. рубильник 2 не замкнут):

iL(0-)=iL(0+)=i1(0+)=0A

i1св(0+)=0А-2А=-2А

Теперь составим выражение для входного сопротивления относительно зажимов ab:

Теперь заменив в этом выражении jw на p и приравняв его нулю получим характеристическое уравнение:

Т .к. характеристическое уравнение имеет один корень, то:

П остоянная интегрирования А определяется по значению свободного тока i1св(0+):

И тогда выражение для тока i1 имеет вид:

И в конце найдем постоянную времени этого переходного процесса:

Теперь, в момент времени t=т, замыкается рубильник 2 и начинается второй переходный процесс. Найдем выражение для токов i1 и i2 в этом случае. Но теперь не все начальные условия нулевые:

i1(0-)=i1(т)=1,265A

UС(0-)=0B

i

i3

с

1пр по-прежнему равно 2А, т.к. постоянный ток через конденсатор не течет, ток в ветви с индуктивностью не может измениться скачком по 1 закону коммутации, следовательно i1(0-)= i1(0+)=1,265А и тогда:

i1св(0+)=1,265А-2А=-0,74А

С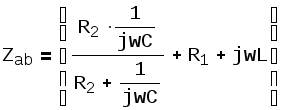 оставим выражение для входного сопротивления относительно зажимов ab в этом случае:

Т еперь заменив в этом выражении jw на p и приравняв его нулю получим характеристическое уравнение:

Привидя это уравнение к общему знаменателю и приравняв числитель нулю получим:

Э то уравнение имеет следующие корни:

Т.к. мы имеем два комплексно сопряженных корня, то характер свободного процесса описысывается следующей формулой:

В этой формуле –y=-200 и w0=400 (из решений характеристического уравнения). Определение А и ф в этом случае проводят по значениям

i1св(0+) и i’1св(0+). Продифференциируем выражение для i1св:

Запишем выражения для i1св и i’1св при t=0+:

В этой системе нам не известно только значение i’1св, найдем его, составив уравнение для контура ECR1L по 2-му закону Киргофа:

i1(0+)R1 + Li’1(0+) + UC(0+) = E

Перейдем от этого уравнения к уравнению для свободных токов:

i1св(0+)R1 + Li’1св(0+) + UCсв(0+) = 0

Здесь нам не известно только UCсв(0+), найдем его:

UC(0-)= UC(0+)=0B

UC = UCпр + UCсв

UCпр= i1прR2 = 80В

UCсв(0+)= UC(0+)- UCпр=0B-80B=-80B

Теперь найдем i’1св(0+):

-0,7410 + 0,05 i’1св(0+) – 80 = 0

i’1св(0+)=1748

Теперь найдем А и ф:

Аsinф = -0,74,

-Аysinф + Aw0cosф = 1748.

Решая эту систему получим, что А = 4,06 и ф = -10,49. И тогда выражение для тока i1 при втором переходном процессе имеет вид:

Теперь найдем выражение для тока i2. Для этого вначале найдем выражение для UС, а потом продифференциировав это выражение по времени получим выражение для i2.

Т .к. мы имеем два комплексно сопряженных корня, то характер свободного процесса UСcв описысывается следующей формулой:

З десь также –y=-200 и w0=400, и для того чтобы найти А1 и ф1 необходимо решить систему:

Чтобы ее решить нам необходимо вычислить U’Cсв(0+), а для этого вначале вычислим i2св(0+), составив систему уравнений для свободных токов, состаящую из двух уравнений, одно из которых мы составим по 1-му закону Киргофа для узла С, а второе по 2-му закону Киргофа для контура ER2R1L:

i3св(0+)R2 + R1i1св(0+) + Li’1св(0+) = 0,

i1св(0+) = i2св(0+) + i3св(0+).

40i3св(0+) - 100,74 + 17480,05 = 0,

i1св(0+) = i2св(0+) + i3св(0+).

Решая эту систему получим, что i3св(0+) = -2A и i2св(0+) = 1,26.

I2св(0+) = СU’Cсв(0+)

1,26 = 12510-6U’Cсв(0+)

U’Cсв(0+) = 10080В

Теперь найдем А1 и ф1:

А1sinф1 = -80,

-А1ysinф1 + A1w0cosф1 = 10080.

Решая эту систему получим, что А1 = -81,36 и ф1 = 79,51. Тогда:

И тогда выражение для тока i2 выглядит следующим образом:

i2 = CU’c = 12510-6(-81,36(-200)e-200tsin(400t+79,51) - 81,36 

 400e-200tcos(400t+79,51)) = 2,034e-200t( sin(400t+79,51)-2 

 cos(400t+79,51)) = 4,55  e-200t  sin(400t+16,07).

  1. Во-втором задание мы найдем выражение для тока i2 при втором переходном процессе операторным методом:

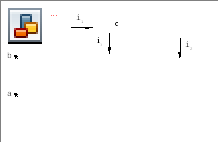
Составим систему уравнений для изображений токов по законам Киргофа для послекоммутационной схемы, изображенной слева (составим по 1-ому закону Киргофа уравнение для узла С и два уравнения по 2-му закону Киргофа для контуров ECR1L и ER2R1L) и найдем выражение для изображения тока I2:

Решая эту систему получим (здесь i1 = 1,265А – начальный ток при втором переходном процессе, который мы вычислили в пункте 1):

Уравнение М(р)=0 имеет корни:

И тогда

N(p1)= 0,4365 + 0,127j = 0,455e16,2j (вычисляем значение числителя при р = р1, а затем переводим его в показательную форму )

N(p2)= 0,4365 - 0,127j = 0,455e-16,2j (вычисляем значение числителя при р = р2, а затем переводим его в показательную форму)

M’(p)= 2LCR2p + R1R2C + L (производная знаменателя)

M’(p1)= 0,2j = 0,2e90j (вычисляем значение знаменателя при р = р1, а затем переводим его в показательную форму)

M’(p2)= -0,2j = 0,2e-90j (вычисляем значение знаменателя при р = р2, а затем переводим его в показательную форму)

Теперь от изображения I2 перейдем к его оригиналу i2, воспользовавшись формулой разложения:

В нашем случае формула примит вид:

Воспользовавшись формулой Эйлера упростим выражение в квадратных скобках:

И наконец запишем окончательное выражение для оригинала i2, при этом переведя cos в sin, воспользовавшись тригонометрической формулой cos = sin(90+):

  1. Вычислим практическую длительность второго колебательного процесса:

Т еперь вычислим период свободных затухающих колебаний:

Найдем логарифмический декремент затухания:

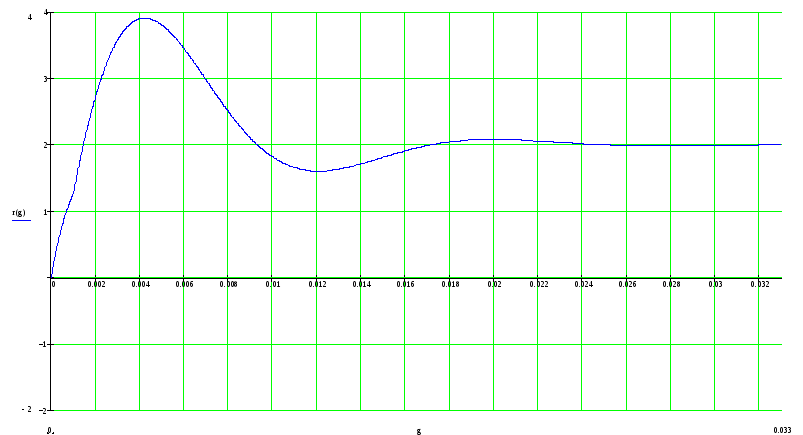
  1. З десь построен график i1(t) для обоих переходных процессов (смотрите следующую страницу):

9

Соседние файлы в папке Домашние работы по Электротехнике
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности