Московский Государственный Институт Электроники и Математики

(технический университет)

Домашнее задание № 2

по электротехнике

Переходные процессы

Проверил: Выполнила:

Артамонов А. Т. студентка группы С-33

Федяшина Ю. А.

Москва-2002

Задание.

Схема №20Б.

В заданной схеме E=100В /постоянная э.д.с./ или J=10А /постоянный ток/, остальные параметры указаны в таблице числовых вариантов.

В момент времени t=0 коммутирует рубильник 1, а через промежуток времени t1 – рубильник 2. t1 принять равным постоянной времени первоначального переходного процесса /если процесс имеет две постоянных времени, то большей постоянной времени/, или периода свободных колебаний, если первоначальный процесс колебательный /t1 можно округлить/.

Требуется определить:

1. Выражения для токов i1(t) и i2(t) классическим методом.

2. Ток i2(t) операторным методом.

3. Практическую длительность второго переходного процесса, а в случае колебательного характера этого процесса также и период свободных колебаний и логарифмический декремент колебаний.

4. Построить график i1(t) для обоих переходных процессов, причем оба переходных процесса должны быть расположены один за другим по оси времени.

№ группы	Вариант схемы	R1 Ом	R2 Ом	R Ом	L мГн	C мкФ
3	Б	8	50	20	80	200

Эквивалентные преобразования схемы:

J- вырожденный источник тока (Rвн.=)

E=J*R2

E=10*50=500В

Преобразованная схема:

Задание 1.

1.Анализ цепи после первой коммутации.

1.1.Анализ цепи до коммутации.

i1(0_)=0

U_c(0_)=0

1.2. Определение независимых начальных условий.

i1(0₊)=i1(0_)

U_c(0₊)=U_c(0_)

1.3. Составление дифференциального уравнения цепи после коммутации.

В торой закон Кирхгофа:

1 .4. Анализ установившегося режима в цепи после коммутации (при t=t1). В результате находим принужденную составляющую (частное решение дифференциального уравнения).

i 1=const 

1.5. Определяем свободную составляющую. Составляем характеристическое уравнение цепи, находим его корни.

где - постоянная времени первого переходного процесса.

i1_св.=Ae^Pt=Ae^-t/

1 .6. Находим общий вид решения неоднородного уравнения (y=yсв.+yпр.)

1 .7. Определение постоянных интегрирования. (Их находим по начальным условиям).

1 .8. Определение реакции цепи, соответствующей заданным начальным условиям.

2.Анализ цепи после второй коммутации.

t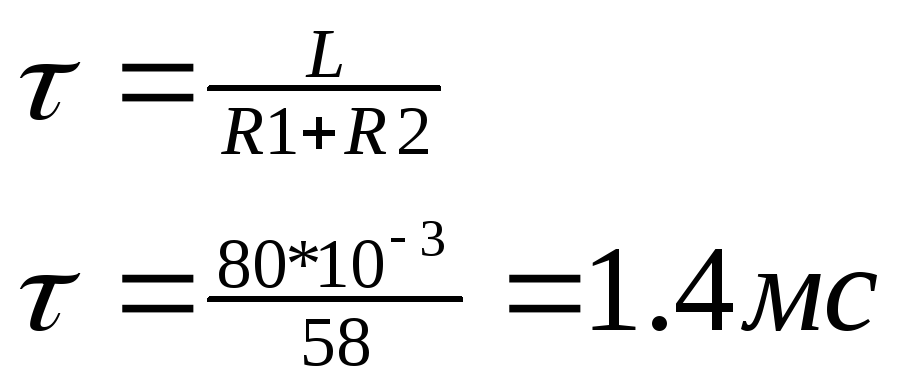 1= (по условию)

2.1. Анализ цепи до коммутации.

U _c(t1_)=0

2.2. Определение независимых начальных условий.

2 .3. Составление дифференциального уравнения цепи после коммутации.

Применим метод узловых и контурных уравнений:

-m=3 (количество ветвей)

-n=2 (количество узлов)

-составляем n-1=1 уравнение по I з. Кирхгофа.

Первый узел:

i3=i1+i2

- составляем [m-(n-1)]=2 уравнения по II з. Кирхгофа.

- полученная система уравнений:

2.4. Анализ установившегося режима в цепи после коммутации (при t=). В результате находим принужденную составляющую ( частное решение дифференциального уравнения).

i2_пр.=0

2 .5. Определяем свободную составляющую. Составляем характеристическое уравнение цепи, находим его корни.

D =-1792*10^-4

P1,2=-jсв., где св.-частота свободных колебаний.

2.6.Находим общий вид реакции цепи.

I = i_пр + i_св

2.7.Определение постоянных интегрирования.

I1(t1₊) = =Aexp(P1t1) + Bexp(P2t1) +

I2(t1₊) = i3(t1₊) – i1(t1₊) = 1.4-

-1.4 = R2C(P1Aexp(P1t1) + P2Bexp(P2t1))

2.8. Определение реакции цепи, соответствующей заданным начальным условиям.

I1(t) =13.706/j*exp((363+j*228)*t) + 127.466*exp((363-j*228)*t) + 8.62

I2(t)=10^-2(363+j*228)*exp((363+j*228)*t)+10^-2(363-j*228) *exp((363-j*228)*t)

Задание 2.

1.Анализ переходных процессов после первой коммутации.

1.1.Анализ цепи до коммутации.

I1(0_)=0

U_c(0_)=0

1.2.Составление операторной эквивалентной схемы цепи после коммутации. Для этого все элементы цепи заменяем их операторной схемой замещения.

1.3.Составляем уравнение в операторной форме.

1 .4. Решаем уравнение.

1.5. От операторных выражений переходим к функциям времени.

2. Анализ переходных процессов после второй коммутации.

2.1. Анализ цепи до коммутации.

i3(t1_)=i1(t1_)=E/(R1+R2)*(1-exp(-t1/)=5.4A

u_c(t1_)=0

2.2. Составление операторной эквивалентной схемы цепи после коммутации. Для этого все элементы цепи заменяем их операторной схемой замещения.

2.3. Составление уравнений в операторной форме.

Метод контурных токов:

I1(p)-контурный ток первого контура

I2(p)-контурный ток второго контура

I2(p)=

N(p) = (E*L – i1(t_)*L*R2)*p + E*R1

M(p) =

P1 =363+j*228

P2 =363-j*228

i2(t)=10^-2(363+j*228)*exp((363+j*228)*t)+10^-2(363-j*228)*exp((363-j*228)*t)

Задание 3.

Практическая длительность второго переходного процесса равна 7 мс.

Период свободных колебаний равен 28 мс

Логарифмический декремент затухания равен 3.6.

Задание 4.