МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И

МАТЕМАТИКИ

( ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ )

ДОМАШНЕЕ ЗАДАНИЕ №4

по курсу “Электротехника ”

Исполнитель: Руководитель:

Студентка Александрова И.Н. Артамонов А.Т.

Группа С - 32

Москва 2002 г.

Исходные данные:

E = 100 B;

R1 = 100 Ом;

R2 = 25 Ом ;

L = 288 мГн;

C = 34.7 мкФ.

Задание 1.Определение выражений для токов i1(t) и i2(t) классическим методом.

А) Анализ переходных процессов после первой коммутации.

1. Анализ цепи до коммутации.

I1(0_)=0

Uc(0_) = 0

2. Определение независимых начальных условий.

I1(0₊) = I1(0_)

Uc(0₊) = Uc(0_)

3. Составление дифференциального уравнения цепи после коммутации.

Запишим второй закон Кирхгофа для контура:

4. Анализ установившегося режима в цепи после коммутации при t=t1_, в результате находим принужденную составляющую (частное решение дифференциального уравнения).

i1_пр =

5. Определение свободной составляющей. Для этого составляем характеристическое уравнение цепи и находим его корни.

- постоянная времени первого переходного процесса

i1_св = Ae^Pt = A*exp

6. Находим общий вид реакции цепи.

I1 = i1_пр + i1_св = A*exp +

7. Определение постоянных интегрирования.

8. Определение реакции цепи соответствующей заданным начальным условиям.

Б) Анализ переходных процессов после второй коммутации.

Время t1, через которое коммутирует рубильник 2 равно постоянной времени первого переходного процесса = 2.3 мс.

1. Анализ цепи до второй коммутации.

= 0.5 А

2. Определение независимых начальных условий.

3. Составление дифференциального уравнения цепи после коммутации.

Воспользуемся методом узловых и контурных уравнений:

1) количество ветвей – m=3;

2) количество узлов – n=2;

3) записываем (n-1) = 1 уравнение по первому закону Кирхгофа

i1 = i2 + i3;

4) выбираем контуры и составляем (m-(n-1)) = 2 уравнения по второму закону Кирхгофа

5) получаем систему уравнений

4. Анализ установившегося режима в цепи после коммутации при t=, в результате находим принужденную составляющую (частное решение дифференциального уравнения).

i2_пр = 0

i1_пр = i3_пр =

5. Определение свободной составляющей. Для этого составляем характеристическое уравнение цепи и находим его корни.

LR2CP² + (L + R1R2C)P + R1 + R2 = 0

P1 = -500.681 P2 = -999.279

6. Находим общий вид реакции цепи.

I = i_пр + i_св

7. Определение постоянных интегрирования.

Uc(t1₊) = i1(t1₊)R2 – E

I1(t1₊) = =Aexp(P1t1) + Bexp(P2t1) +

I2(t1₊) = i1(t1₊) – i3(t1₊) = - 0.5 А

0.5 - = R2C(P1Aexp(P1t1) + P2Bexp(P2t1))

A = -5.188 A

B = 48.394 A

8. Определение реакции цепи соответствующей заданным начальным условиям.

I1(t) = -5.188*exp(-500.681*t) + 48.394*exp(-999.279*t) + 0.8

I2(t) = -0.712*exp(-500.681*t) + 4.195*exp(-999.279*t)

Задача2. Определить ток i2(t) операторным методом.

А) Анализ переходных процессов после первой коммутации.

1. Анализ цепи до коммутации.

I1(0_)=0

Uc(0_) = 0

2. Составление операторной эквивалентной схемы цепи после первой коммутации.

3. Составляем уравнение в операторной форме.

= I1(p)*(Z1(p) + Z2(p) + Z_l(p)) = I1(p)*(R1 + R2 + pL)

5. Решаем полученное уравнение.

I1(p) =

6. От операторных выражений переходим к функциям времени.

 1- exp(-t)

I1(p) =

Б) Анализ переходных процессов после второй коммутации.

1. Анализ цепи до второй коммутации.

= 0.5 А

2. Составляем операторную эквивалентную схему цепи после второй коммутации.

3. Составляем уравнения в операторной форме.

Составляем уравнения по методу контурных токов.

I_i(p), I_ii(p) – операторные контурные токи.

Умножим второе уравнение на , сложим с первым и выразим I_ii(p)

I_ii(p) = =

=

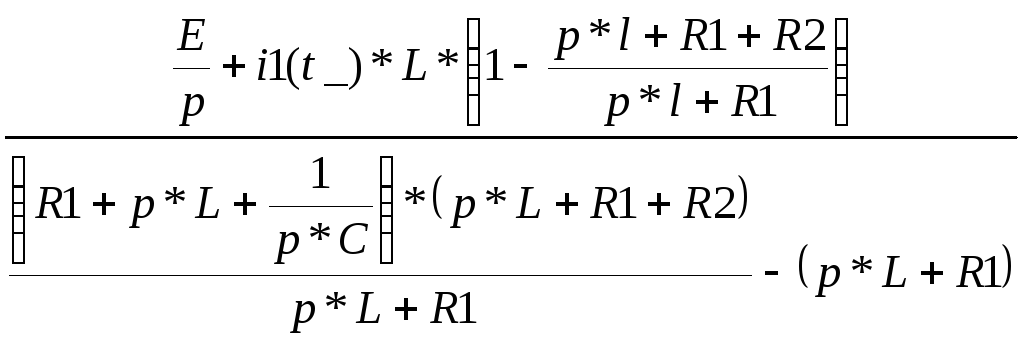I2(p) = I_ii(p)

N(p) = (E*L – i1(t_)*L*R2)*p + E*R1

M(p) =

P1 = -500.681 P2 = -999.279

M¹(p) = 2L*R2*p + R1*R2 +

M¹(p1) = 3589.905

M¹(p2) = -3589.906

N(p1) = -2617.161

N(p2) = -15181.831

i2(t) = -0.729*exp(-500.681*t) + 4.229*exp(-999.279*t)

Задание 3. Определить практическую длительность второго переходного процесса.

1 = 2 мс 2 = 1 мс

Практическая длительность второго переходного процесса равна 5, то есть 10 мс.

З адание4. Построить график i1(t) для обоих переходных процессов.

8