5.2 Счетчики с последовательным переносом

5.2.1 Последовательный суммирующий счетчик

Как следует из таблицы 5.1 самый младший разряд Q0 меняет свое состояние с каждым счетным импульсом, смена состояния каждого последующего разряда происходит, если предыдущий переходит из единичного в нулевое состояние. Если использовать Т-триггеры, соединенные так, как показано на рисунке 5.1, то получим именно такую последовательность смены состояний триггеров.

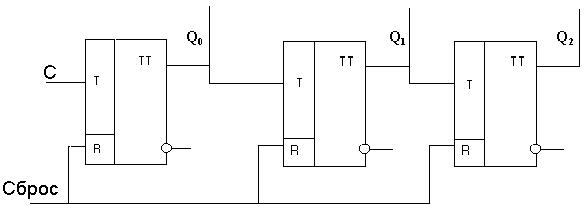
Рисунок 5.1- Последовательный суммирующий счетчик

На рисунке 5.2 показаны временные диаграммы работы суммирующего счетчика

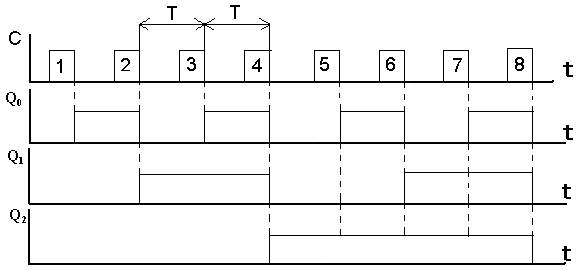
Рисунок 5.2- Временные диаграммы работы суммирующего счетчика

Каскадное включение п таких триггеров образует счетчик с коэффициентом счета Ксч = 2n. При этом необходимо помнить, что каждый триггер обладает Ксч = 2, а при их последовательном соединении коэффициенты счета перемножаются. На рисунке .2 видно, что период следования импульсов после каждого триггера увеличивается вдвое, и после последнего превышает период входных импульсов в Ксч раз. Соответственно частота уменьшается в такое же количество раз, т.е. делится на число, равное Ксч. Это свойство положено в основу использования счетчиков в качестве делителя частоты.

5.2.2 Последовательный вычитающий счетчик

Возможен и другой вариант последовательного включения триггеров, когда их входы соединены с инверсными выходами предшествующих триггеров, как показано на рисунке 5.3. Так получают двоичный вычитающий счетчик, смена состояний которого показана в таблице 5.2.

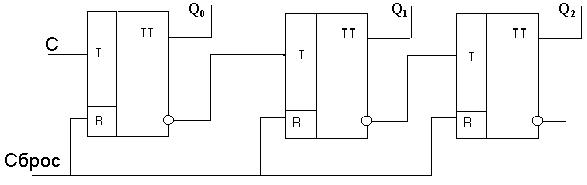
Рисунок 5.3 - Последовательный вычитающий счетчик

На рисунке 5.4 показаны временные диаграммы работы вычитающего счетчика.

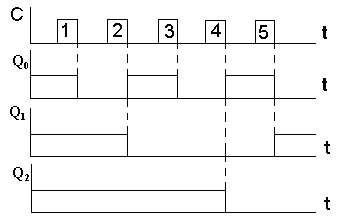
Рисунок 5.4- Временные диаграммы работы вычитающего счетчика

На рисунках 5.1 и 5.3 показаны схемы двоичных последовательных счетчиков, т. е. таких счетчиков, в которых при изменении состояния определенного триггера возбуждается последующий триггер, причем триггеры меняют свои состояния последовательно.

Если в данной ситуации должны изменить свои состояния п триггеров, то для завершения этого процесса потребуется п интервалов времени, соответствующих времени изменения состояния каждого из триггеров. Такой последовательный характер работы является причиной двух недостатков последовательного счетчика:

- меньшая скорость счета по сравнению с параллельными счетчиками,

- возможность появления ложных сигналов на выходе схемы.

Допустимая скорость счета в счетчиках обоих типов определяется максимальной скоростью переключения одного триггера.

Определяя максимальную скорость счета последовательного счетчика, следует учитывать наиболее неблагоприятный случай изменения состояния всех т триггеров. Суммарную продолжительность переходного процесса можно определить как сумму времен запаздывания отдельных элементов, соединяющих триггеры, и времен срабатывания всех триггеров. Найденное таким образом максимальное время перехода счетчика из одного состояния в другое следует считать предельным. Обычно реальное время перехода меньше предельного, так как в ряду последовательно включенных триггеров данный триггер начинает переход из одного состояния в другое еще до окончания переходного процесса в возбуждающем его элементе.

Последовательный характер переходов триггеров счетчика является источником ложных сигналов на его выходах. Например, в счетчике, ведущем счет в четырехразрядном двоичном коде с «весами» 8421, при переходе от числа 710 = 01112 к числу 810 = 10002 на выходе появится следующая последовательность сигналов: 0111– 0110 – 0100 – 0000 – 1000. Это означает, что при переходе из состояния 7 в состояние 8 на выходах счетчика на короткое время появятся состояния 6; 4; 0. Эти дополнительные состояния могут вызвать неправильную работу других устройств.