Некоммерческое акционерное общество

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

 

Кафедра электроснабжения промышленных предприятий

 

 

 

 

 

 

 

 

МАТЕМАТИЧЕСКИЕ ЗАДАЧИ И

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ В ЭЛЕКТРОЭНЕРГЕТИКЕ

 

Методические указания и задания к расчетно-графической работе № 1

(для студентов очной формы обучения специальности 050718 – Электроэнергетика)

 

 

 

 

 

 

 

 

 

 

 

Алматы 2006

СОСТАВИТЕЛЬ: Н.А. Туканова. Методические указания и задания к расчетно-графической работе № 1 (для студентов очной формы обучения специальности 050718 – Электроэнергетика). – Алматы: АИЭС, 2006. – 20 с.

 

 

 

 

Данная разработка включает задания на расчетно-графическую работу №1 и методические указания по их выполнению, а также список необходимой литературы.

Ил. 1, табл.11, библиогр. - 12 назв.

 

 

Рецензент: канд. техн. наук, доцент С.А. Бугубаев.

 

 

 

 

 

Печатается по плану издания Алматинского института энергетики и связи на 2006 год.

 

 

 

 

 

Алматинский институт энергетики и связи, 2006 г.

С одержание

 

 

Введение	4
1 Задание № 1. Решить систему линейных уравнений графическим методом. Построить область допустимых решений и определить точку экстремума функции	4
2 Задание № 2. Методом неопределенных множителей Лагранжа определить оптимальную реактивную мощность синхронных двигателей	8
3 Задание № 3. Определить вероятность нагрузки трансформаторов питающей подстанции; математическое ожидание, дисперсию, среднеквадратичное отклонение случайной величины нагрузки трансформатора; показатели надежности системы электроснабжения относительно шин 0,4 кВ; величину недоотпущенной электроэнергии за год относительно шин 0,4 кВ	14
Список литературы	19

 

 

 

 

 

 

 

 

 

 

Введение

Согласно учебному плану, студенты, обучающиеся по специальности 050718 – Электроэнергетика, изучают курс «Математические задачи и компьютерное моделирование в электроэнергетике», в котором предусмотрены две расчетно-графические работы, состоящие из трех заданий каждая и предполагающие самостоятельное закрепление студентами пройденных разделов дисциплины.

К сдаче экзамена по курсу студенты допускаются после успешного выполнения и защиты расчетно-графических работ.

 

 

1 Задание № 1

Решить систему линейных уравнений графическим методом. Построить область допустимых решений и определить точку экстремума функции, согласно заданию.

Исходные данные для задачи принимаются по таблице 1.1, согласно правилам выбора вариантов.

 

Таблица 1.1 - Исходные данные

Начальная буква фамилии студента	А, Д	Б, Е	В, Г, Я	Ж, З, И, Л	К, Ю	М, О	Н, П	Р, Т, У, Ф	С, Ч, Ц	Х, Ш, Щ, Э
Элементы целевой функции
C1	1	2	1	-1	5	2	2	1	-4	5
C2	-2	1	5	3	2	1	3	-2	5	1
C3	3	-1	4	2	-1	-1	6	-3	6	-3
C4	10	-1	-6	-	-	-1	3	-	-	1
f(x)	max	min	max	min	max	min	max	min	max	min

 

1.1 Методические указания

Решение систем линейных уравнений графическим методом.

В системе координат х₂´х₁ неравенство определяет полуплоскость с граничной прямой а₁х₁ + а₂х₂ = а₀.

Если задана система неравенств, то для построения области допустимых решений (ОДР) строят граничные прямые, далее определяются полуплоскости, где выполняются данные неравенства.

Чтобы получить координаты ОДР (вершин), необходимо решить систему уравнений прямых, пересекающихся в этих вершинах.

При числе n>2 неравенство

а₁х₁ + а₂х₂ + ...+ a_nx_n £ а₀ эквивалентно уравнению

а₁х₁ + ...+ a_nx_n + x_n+1 = a₀; x_n + 1 ³ 0 и

а₁х₁ + ...+ a_nx_n ³ 0.

Аналогично а₁х₁ + ... + a_nx_n - x_n+1 = 0.

Переменную x_n+1 называют дополнительной (балансовой).

Если задана система неравенств

,

то ее можно заменить эквивалентной системой линейных уравнений с (n+m) переменными.

,

причем x_n+1³0, ..., x_n+m³0.

Вектор - потенциал , перпендикулярный к прямым базисных переменных, указывает направление скорейшего возрастания функции f, вектор - направлен в наискорейшем убывании функции f.

Данная задача решается с помощью программы Mathcad. Для этого необходимо ввести данные из таблицы 1.1, соответствующие уравнению функции, и из таблицы 1.2, соответствующие уравнениям ограничений. Задать требования по выполнению принципа неотрицательности полученных решений. Построить на графике область допустимых решений и вектор-потенциал, по его направлению определить точку экстремума функции и ее координаты. Определить значение функции и переменных в точке экстремума.

 

Таблица 1.2 - Исходные данные

		Последняя цифра № зач. кн.
		Элементы Ai, Bj ,Cij	0	1	2	3	4	5	6	7	8	9
Источники, потребления и стоимость передачи единицы мощности	Мощность источников, Aij	a11	1	2	1	1	2	1	2	-1	1	6
		a12	1	3	-1	1	1	1	-1	1	2	-1
		a13	2	-4	2	2	1	2	1	2	-3	4
		a14	-6	-5	-1	-	-	-1	2	-	-	2
		a21	1	5	2	2	3	2	2	1	4	-9
		a22	1	-6	1	-3	2	1	1	-5	6	8
		a23	4	1	-3	1	1	-3	1	-1	2	7
		a24	-8	-1	1	-	-	1	1	-	-	1
		a31	4	4	1	2	5	1	-1	1	2	-4
		a32	2	1	1	-5	3	1	4	1	-3	5
		a33	1	-2	1	6	4	1	-2	3	1	6
		a34	-4	3	1	-	-	1	-2	-	-	1
	Мощность потребителей, Bj	b1	1	1	2	-5	5	2	1	2	4	5
		b2	1	3	6	3	6	6	2	1	10	7
		b3	3	2	7	5	7	7	3	5	1	8
		b4	-	-	-	-	-	-	-	-	-	-
	Знаки ограничений ( ≤ ; ≥; =)	1	=	≤	=	≥	≤	=	≤	≤	=	≤
		2	=	≤	=	≤	=	=	≤	≤	=	≥
		3	=	≤	=	≤	≥	=	≤	≤	=	≥

 

1.2 Пример

f(x₄, x₅)=4x₄+x₅

Given

5x₁-2x₂+2x₃+x₄-x₅=13

2x₁-2x₂+x₃-x₄+x₅=5

x₁+2x₂+4x₄-2x₅=5

Далее необходимо построить выражения уравнений ограничений в зависимости от х₄ и х₅.

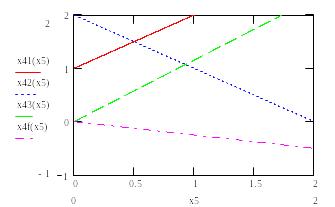
Строим график.

По графику определяем направление вектор - потенциала, который в данном случае имеет координаты (0,0) и (4,1); далее строим перпендикуляр к этому вектору, по которому мы узнаем направление наискорейшего возрастания функции. Первая точка пересечения перпендикуляра с ОДР, будет являться min функции, а последняя - max. В нашем случае: min f (0,0), а max f (1,1). По полученным значениям определяются все переменные и значение функции в точке экстремума.

 

 

2 Задание № 2

К шинам РУ 6-10 промышленного предприятия присоединены N синхронных электродвигателей, требуется с помощью метода неопределенных множителей Лагранжа определить оптимальную реактивную мощность от каждого из синхронных двигателей, пренебрегая сопротивлениями кабелей. Реактивная нагрузка, подлежащая компенсации на стороне 6-10 кВ, определяется вариантом задачи. Данные к задаче для каждого из вариантов принимаются по таблицам 2.1, 2.2 и 2.3. Технические характеристики двигателей приведены в таблице 2.4.

 

Таблица 2.1 – Исходные данные

Удельная стоимость	Предпоследняя цифра номера зачетной книжки
	0	1	2	3	4	5	6	7	8	9
сo (у.е./кВт)	55	60	65	70	75	50	72	68	80	73

 

Таблица 2.2 – Исходные данные

Мощность, подлежащая компенсации	Последняя цифра номера зачетной книжки
	0	1	2	3	4	5	6	7	8	9
QА, Мвар	1,4	1,6	1,3	1,5	1,2	0,8	0,9	1,5	1,2	0,8

Таблица 2.3 – Исходные данные

Кол-во и пара-метры СД	Начальная буква фамилии
	А, Д	Б, Е	В, Г, Я	Ж,З, И, Л	К, Ю	М, О	Н,П	Р, Т, У, Ф	С, Ч, Ш	Х,Ц, Щ, Э
N	4	5	6	4	5	5	4	4	4	4
Uн(кВ)	6	6	10	6	6	10	10	10	6	6
Рн(кВт	1000	2500	3200	6300	800	1250	4000	1600	400	6300
n об/мин	1000	750	750	1000	750	1000	750	1000	500	1000
	600	500	600	750	500	600	600	600	300	750
	500	600	500	600	375	500	500	375	187	600
	250	250	375	500	300	300	1000	250	167	500
		300	300		167	250
			250