Случайные величины и законы их распределения

Случайным событием называется такое событие, исход которого заранее не предсказуем с абсолютной точностью. Даже если опыты и испытания по изучению возможных исходов событий проводятся многократно и в одних и тех же условиях, их результаты непостоянны. Однако при массовых экспериментах, при изучении массовых процессов и явлений наблюдается некоторая степень устойчивости (статистическая устойчивость) возможных результатов событий. Объективной характеристикой (своеобразным показателем качества) случайных событий является число р, называемое вероятностью события. Аналогично понятие случайности может быть отнесено и к количественной оценке (величине), характеризующей в той или иной степени качество продукции.

Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.

Закон распределения случайной величины х

Показатель качества, Х	х1	х2	…	хn
Вероятность результата, р	р1	р2	…	рn

при этом , где суммирование распространяется на все (конечное или бесконечное) множество возможных значений данной случайной величины X.

Закон распределения непрерывной случайной величины удобно задавать при помощи так называемой функции плотности вероятности f(x). Вероятность р(a < х < b) того, что значение, принятое случайной величиной X, попадет в промежуток (а, b), определяется равенством

Функция плотности вероятности f(x) обладает следу­ющими свойствами:

1. f(x) ³ 0;

2. 

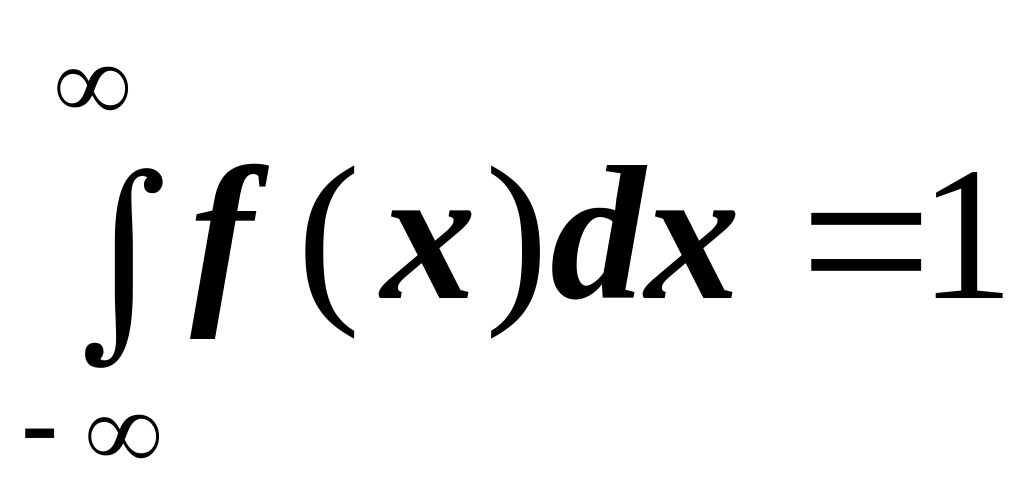
Если все значения случайной величины X заключены в про­межутке (А, В), то последнее условие может быть заменено условием .

Функция F(х) существует как для дискретных, так и для непрерывных случайных величин. Если f(x) - функция плотности распределения вероятности непрерывной случай­ ной величины X, то

F(x) = .

Важнейшие свойства функции распределе­ния вероятности:

1) F (х) — неубывающая функция своего аргумента,

2) F(- оо) = 0,

3) F(+ oo) = l.

f(x)

x

F (х)

x

M(x)

Математическим ожиданием дискретной случайной величины называется сумма произведений значений слу­чайной величины на вероятности этих значений.

Дисперсией случайной величины называют математиче­ское ожидание квадрата отклонения случайной величины от ее математического ожидания:

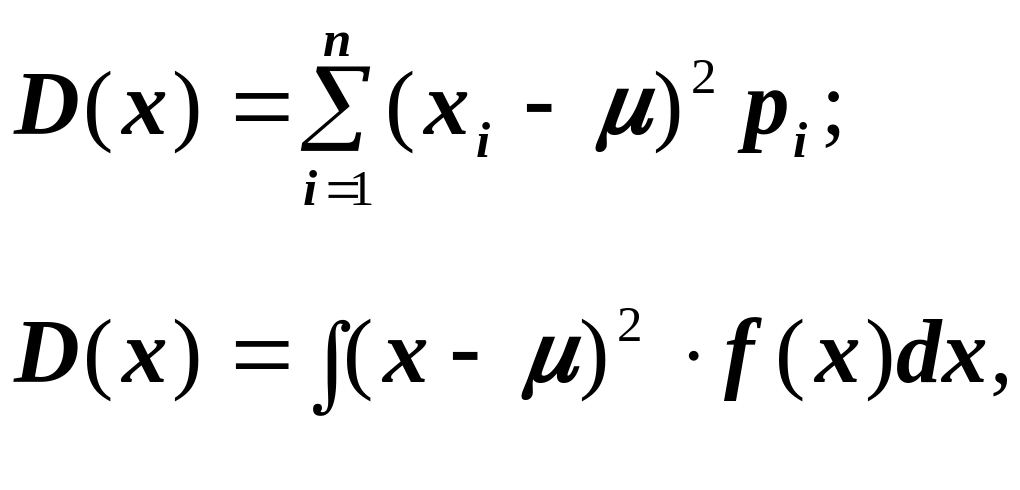
Биномиальный закон распределения. Закон Пуассона

Если вероятность наступления случайного события в каждом испытании равна р, то, как известно, вероятность того, что при п испытаниях событие осуществится т раз, определяется формулой Бернулли:

Закон распределения случайной величины X, могущей принимать п+1 значение (0, 1, ...., п), описываемый формулой Бернулли, называется биномиальным.

Закон распределения случайной величины X, могущей принимать любые целые неотрицательные значения (0, 1, ...., п), описываемый формулой

носит название закона Пуассона.

Математическое ожидание и дисперсия случайных ве­личин, распределенных по биномиальному закону и закону Пуассона, определяются по следующим формулам:

а) биномиальный закон: М (х) = пр; D(x) = npq;

б) закон Пуассона: М(х) = λ; D(x) = λ.