10.2. Основні характеристики рядів динаміки

Завдання статистики полягає в тому, щоб шляхом аналізу рядів динаміки розкрити і охарактеризувати закономірності, що проявляються на різних етапах розвитку того чи іншого явища, виявити тенденції розвитку та їх особливості.

В процесі аналізу динаміки розраховують і використовують наступні аналітичні показники динаміки: абсолютний приріст, коефіцієнт росту, темп росту, темп приросту і абсолютне значення одного відсотка приросту.

Розрахунок цих показників ґрунтується на абсолютному або відносному порівнянні між собою рівнів ряду динаміки. При цьому порівнюваний рівень називається поточним, а рівень, з яким проводять порівняння – базисним. За базу порівняння часто приймають або попередній рівень, або початковий (перший) рівень ряду динаміки.

Якщо кожний рівень порівнюється з попереднім, то отримують ланцюгові показники динаміки, а якщо кожний рівень порівнюють з одним і тим самим рівнем, взятим за базу порівняння, то такі показники називаються базисними.

Абсолютний приріст (∆_у) обчислюється як різниця між поточним та базисним рівнями і показує, на скільки одиниць підвищився або зменшився рівень порівняно з базисним за певний період часу.

або

де ∆_у – абсолютний приріст;

у_і – поточний рівень ряду динаміки;

у₀ – початковий (перший) рівень ряду динаміки;

у_і-1 – попередній рівень ряду динаміки.

Абсолютний приріст зі змінною базою інакше називають швидкістю зростання.

Коефіцієнт зростання (К_з) вираховується як відношення порівнюваного рівня до базисного і показує, у скільки разів порівнюваний рівень більший або менший за базисний

або

Між ланцюговими і базисними коефіцієнтами зростання існує певний взаємозв'язок. Добуток кількох послідовних ланцюгових темпів зростання дорівнює базисному темпу зростання за відповідний період і, навпаки, поділивши наступний базисний темп зростання на попередній, отримаємо відповідний ланцюговий темп зростання.

Темп зростання (Т_з) – це відсоткове вираження коефіцієнта зростання

або

Темп приросту (Т_п ) визначається як відношення абсолютного приросту до абсолютного попереднього або початкового рівня і показує на скільки відсотків порівнюваний рівень більший або менший рівня, прийнятого за базу порівняння.

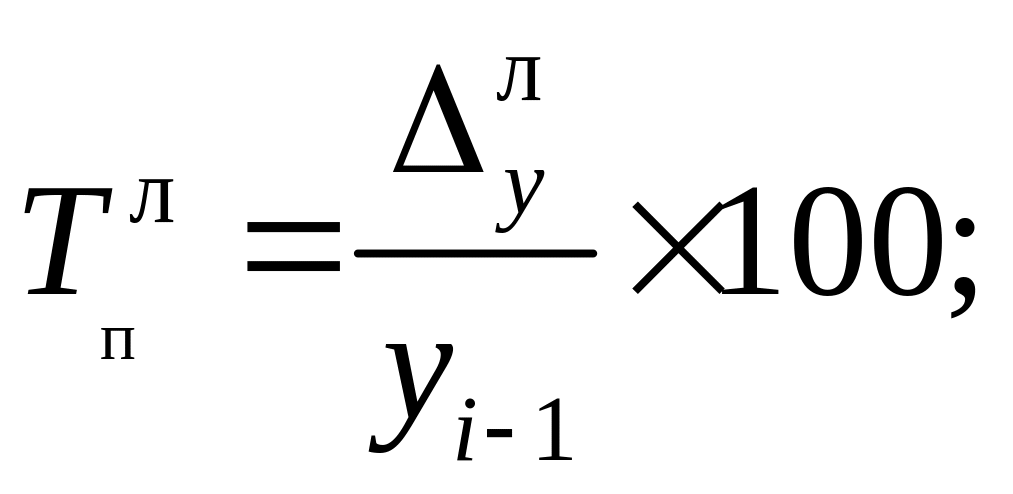
або

або

Абсолютне значення одного відсотка приросту (А) визначається шляхом ділення абсолютного приросту на темп приросту за один і той самий період. Абсолютне значення одного відсотка приросту можна вирахувати технічно більш легким шляхом, діленням початкового рівня на 100.

Подамо приклад розрахунку усіх вищенаведених показників в табл. 10.1.

Таблиця 10.1 – Розрахунок показників динаміки обсягу продукції

за 2005-2010рр.

Роки	Обсяг продукції, тис. грн. (у)	Абсолютний приріст, тис. грн.		Темп зростання, %		Темп приросту, %		Абсолютне значення 1% приросту, тис.грн. (А)
		базисний	ланцюговий	базисний	ланцюговий	базисний	ланцюговий
2005 2006 2007 2008 2009 2010	20 23 27 28 30 33	– 3 7 8 10 13	– 3 4 1 2 3	– 115 135 140 150 165	– 115,0 117,4 103,7 107,1 110,0	– 15,0 35,0 40,0 50,0 65,0	– 15,0 17,4 3,7 7,1 10,0	– 0,20 0,23 0,27 0,28 0,30

Ряди динаміки, як правило подаються не тільки в таблицях, але й показуються на графіках. За графічного зображення динамічного ряду на осі абсцис відкладається шкала часу, а на осі ординат – шкала рівнів ряду (рис. 10.1).

Якщо абсолютна або відносна швидкість динаміки у межах періоду, що вивчається, неоднакова, порівняння однойменних характеристику за різні інтервали часу вимірюється прискорення (уповільнення) динаміки. Різниця абсолютних ланцюгових приростів характеризує абсолютне прискорення (+) чи уповільнення (–) динаміки. Для додатних абсолютних приростів можна визначити відносне прискорення ( ). Якщо інтервали часу неоднакові, використовують середні абсолютні прирости відповідних інтервалів (див. п. 10.3).

Рис. 10.1. Динаміка обсягу продукції за 2005–2010 pp.

На основі темпів зростання або темпів приросту (базисних або середніх) проводять порівняльний аналіз інтенсивності динаміки паралельних рядів, наприклад доходи міського телефонного та мобільного зв’язку.

Таке співвідношення називають коефіцієнтом випередження

або

де – відповідно темпи зростання і темпи приросту порівнювальних рядів динаміки.

За допомогою цих коефіцієнтів можна порівнювати динамічні ряди однакового змісту, але вони відносяться до різних територій (країни, регіони, райони і т.п.) або до різних організацій, або ряди різного змісту, що характеризують один і той же об’єкт.