5.2. Середня арифметична та її властивості

Найбільш поширеним видом середніх величин у статистці є середня арифметична. Середня арифметична застосовується у тому випадку, коли обсяг ознаки, що варіює є сумою індивідуальних її значень. Вона буває простою і зваженою.

Середня арифметична проста застосовується тоді, коли середнє значення ознаки розраховується за незгрупованими одиницями сукупності. Для цього суму індивідуальних значень (обсягу) ознаки, що варіює слід розділити на число цих значень. Якщо індивідуальні значення ознаки позначити через х₁, х₂, ..., хп, а середню арифметичну величину через , то розрахунок її можна представити наступною формулою:

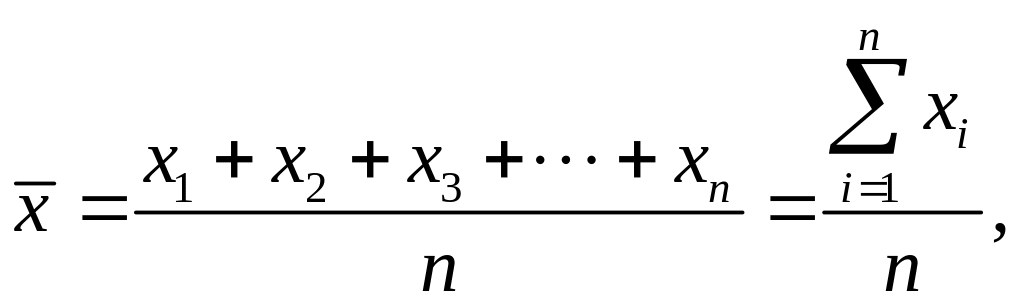
де – середня величина ознак;

х, х₂, х_3,...,х_п – індивідуальні значення ознаки;

∑ (велика грецька літера «сігма») – знак суми;

п – кількість варіантів.

Розглянемо приклад. Необхідно визначити середній стаж роботи 12 працівників відділення поштового зв’язку.

Таблиця 5.1 – Розподіл працівників за стажем

Порядковий номер працівника	1	2	3	4	5	6	7	8	9	10	11	12
Стаж працівника (роки)	6	4	5	3	3	5	5	6	3	7	4	5

роки.

Як видно, середня арифметична може бути дробним числом, якщо навіть індивідуальні значення ознаки задані тільки цілими числами.

Це випливає із сутності середньої арифметичної, яка є величиною абстрактною (теоретичною), тобто вона може приймати таке числове значення, яке не зустрічається у представленій сукупності індивідуальних значень ознаки.

Якщо в сукупності варіанти зустрічаються по кілька разів, то їх об’єднують у групи і, таким чином, переходять від середньої арифметичної простої до зваженої.

Середня арифметична зважена обчислюється як частка від ділення суми добутків варіантів і їх частот на суму частот. Вона визначається за формулою:

де – частоти (ваги), які показують скільки разів зустрічаються значення ознаки в сукупності.

Отже, для обчислення середньої арифметичної зваженої потрібно:

а) кожний варіант перемножити на його частоту;

б) знайти суму їх добутків;

в) суму добутку поділити на суму ваг.

Наведемо приклад. Маємо дані про заробітну плату працівників і чисельність працівників, які отримують дану заробітну плату.

Таблиця 5.2 – Розподіл працівників за заробітною платою

Табельний номер працівника	Заробітна плата одного працівника, грн. (х)	Число працівників, чол. (f)
1 2 3 4 5	1500 1800 2000 2100 2500	10 17 40 18 15
Разом:	×	100

Середня заробітна плата за такими даними становитиме:

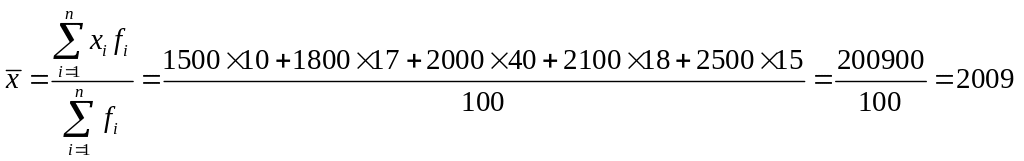грн.

Іноді середні величини потрібно обчислити не з конкретних значень варіантів досліджуваної ознаки, а із значень величин, виражених у вигляді інтервалів. У таких випадках потрібно для кожного інтервалу знайти його середину за простою середньою між верхньою і нижньою межами кожного інтервалу і після цього проводити обчислення за формулою середньої арифметичної зваженої:

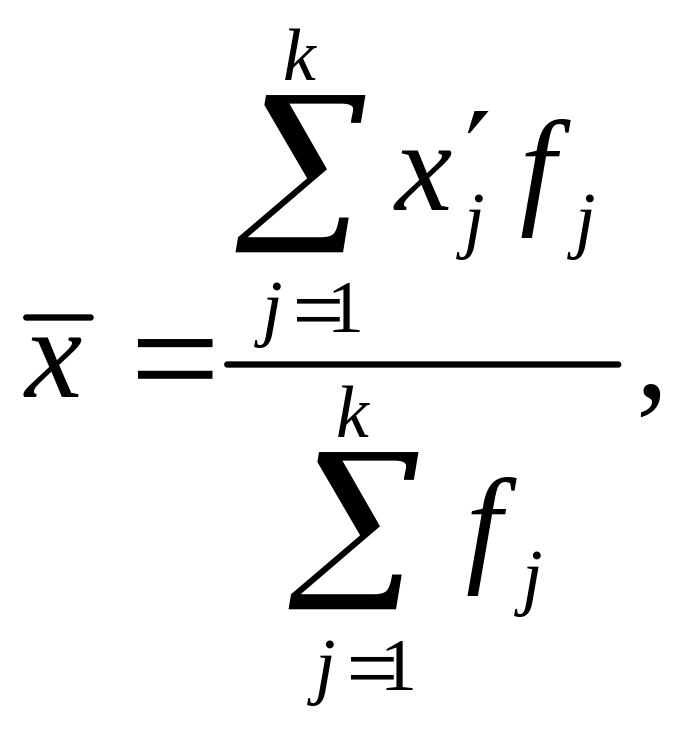
де – середина j-го інтервалу;

k – кількість інтервалів.

У низці випадків замість частот при знаходженні середньої використовують будь-які інші величини. Частоти окремих варіантів можуть бути виражені не тільки абсолютними величинами, але, і відносними величинами – частостями (w_i). Замінивши в даному випадку абсолютні значення частот відповідними відносними величинами, отримаємо той самий результат:

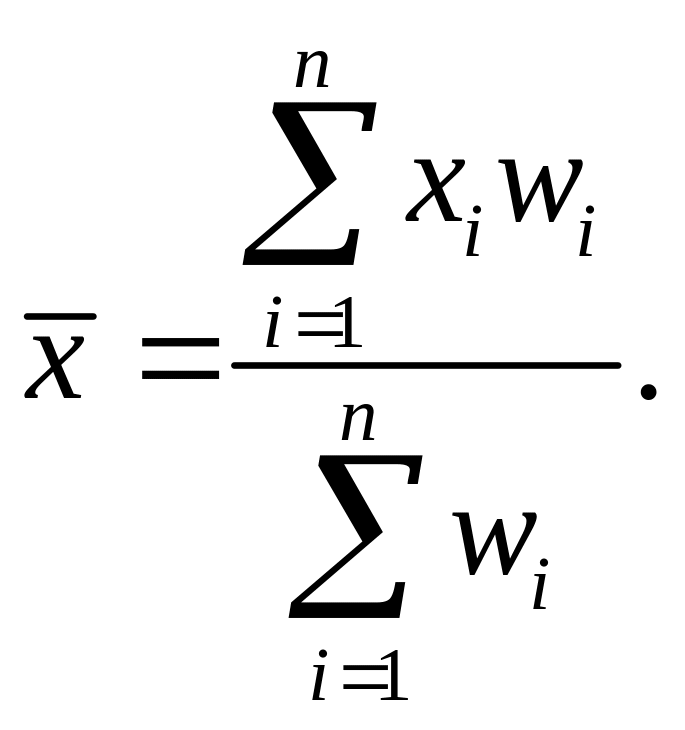
Покажемо обчислення середньої на основі інтервального ряду.

Приклад. Розрахувати середню тривалість заняття телефонної лінії ММТС на добу:

Таблиця 5.3 – Тривалість заняття лінії ММТС

Тривалість телефонних з'єднань, хв. (xj)	Частка населення, % (wj)
До 10	45,0	5	225,0
10 – 20	14,8	15	222,0
20 – 30	13,2	25	330,0
30 – 40	10,5	35	367,5
40 – 50	8,5	45	382,5
50 – 60	4,5	55	247,5
Понад 60	3,5	65	227,5
Разом	100,0	–	2002,0

Для обчислення середньої величини треба в кожному інтервалі визначити серединне значення х', після чого провести зважування звичайним порядком x'w. У закритому інтервалі серединне значення визначається як напівсума значень нижньої і верхньої меж. Іноді завдання визначення середньої за величинами інтервального ряду ускладнюється тим, що невідомі крайні межі початкового і кінцевого інтервалів. У цьому випадку передбачається, що відстань між межами даного інтервалу така ж сама, як і в сусідньому інтервалі.

Середня тривалість заняття телефонної лінії ММТС на добу складе:

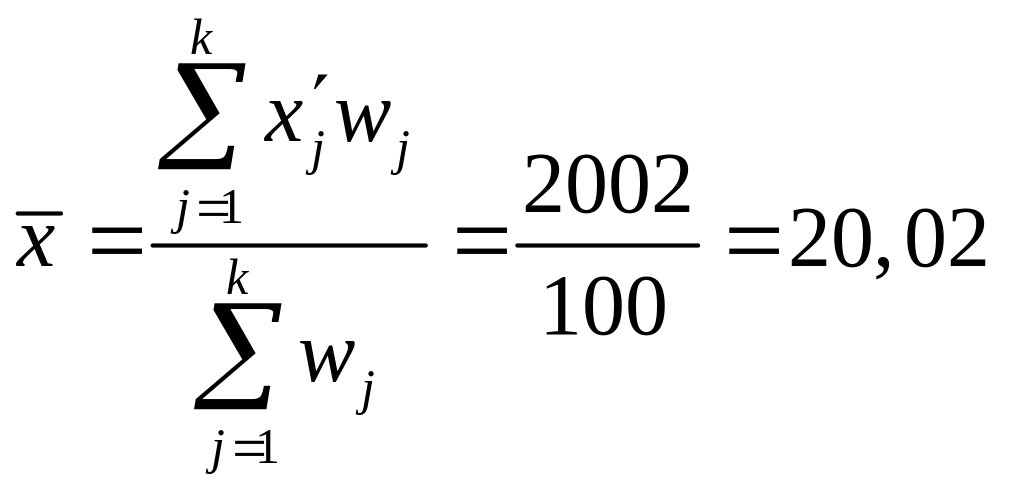хв.

На практиці часто виникає необхідність визначення загальної середньої з групових або приватних середніх. Варіантами у такому разі виступають середні значення ознаки за групою ( ), а вагами – чисельність одиниць кожної групи (f_j). Розрахунок такої середньої здійснюється за формулою середньої арифметичної зваженої, яка за вказаних умов має наступний вигляд:

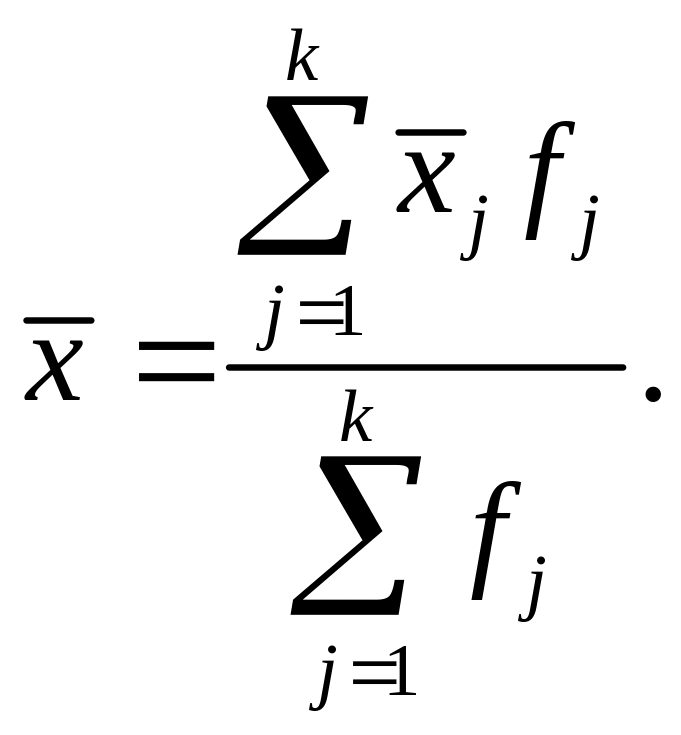
Основні властивості середньої арифметичної. Середня арифметична має деякі математичні властивості, що мають практичне значення для спрощеного обчислення середньої за даними варіаційного ряду:

1. Від зменшення або збільшення частот кожного значення ознаки х в A разів величина середньої арифметичної не зміниться. Якщо всі частоти розділити або помножити на будь-яке число, то величина середньої не зміниться.

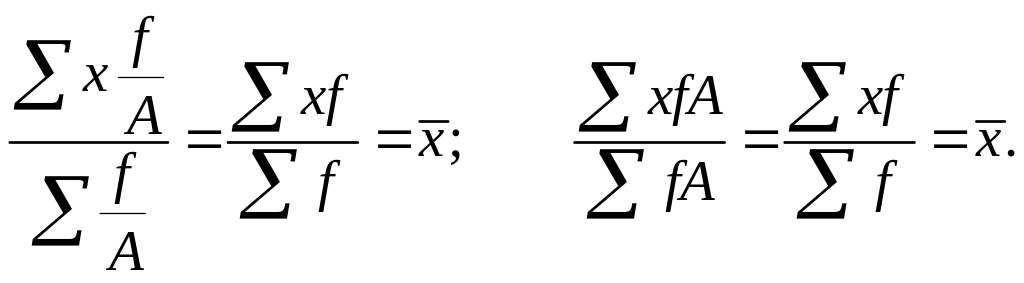
Ця властивість дає можливість частоти замінити питомими вагами, називаними частостями, а також, коли частоти всіх варіантів однакові, обчислювати середні за формулою середньої арифметичної простої. Зазначена властивість важлива тоді, коли абсолютні числа – частоти не відомі, а відомі лише питомі ваги, тобто відносні величини структури сукупності. Тоді середня обчислюється так:

якщо d – в %,

або

якщо d – у частках одиниці.

2. Якщо всі індивідуальні значення ознаки збільшити або зменшити на одне і те ж постійне число А, то і середня зміниться відповідним чином, тобто

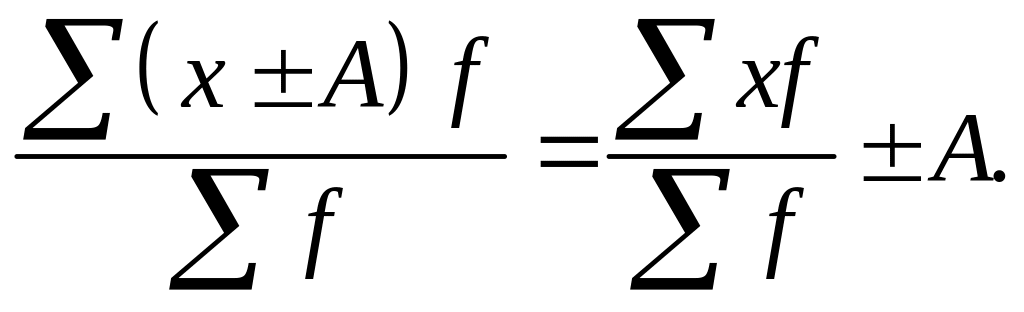
3. Якщо всі індивідуальні значення ознаки збільшити або зменшити в А число разів, то і середня зміниться відповідним чином, тобто

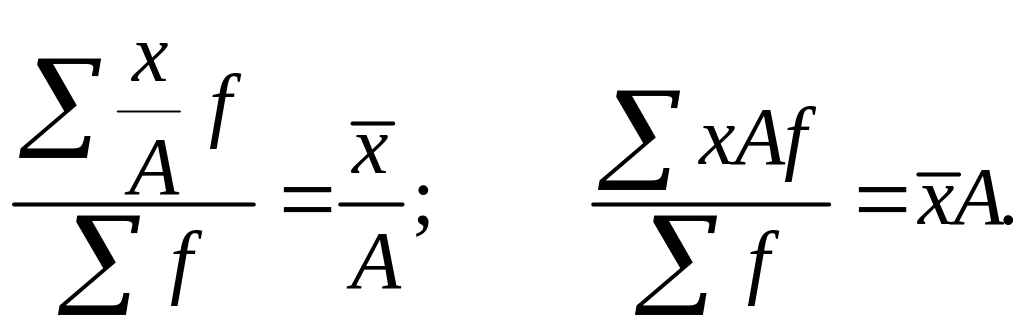
4. Сума відхилень окремих значень ознаки (x) від їх середнього значення ( ) дорівнює 0, тобто

(для середньої арифметичної простої);

(для середньої арифметичної зваженої).

Логічно ця властивість означає, що оскільки середня арифметична є рівнодіючою, то відхилення варіант в один бік від неї компенсується відхиленнями в інший.

Викладені вище властивості середньої арифметичної дозволяють у багатьох випадках спростити її розрахунки: можна з усіх значень ознаки відняти довільну постійну величину, різницю скоротити на загальний множник, а потім обчислену середню помножити на загальний множник і додати довільну постійну величину.