Міністерство освіти України
Чернівецький державний університет імені Юрія Федьковича
МЕТОДИЧНІ ВКАЗІВКИ І ЗАВДАННЯ
ДО ЛАБОРАТОРНИХ РОБІТ З КУРСУ
“ТЕОРІЯ КЕРУВАННЯ ”
Чернівці
ЧДУ
1998
УДК 618.516
Методичні вказівки і завдання до лабораторних робіт з курсу “Теорія керування” / Укл.: Сопронюк Ф.О., Гайдайчук І.В. – Чернівці: ЧДУ, 1998. – 32 с.
Друкується за ухвалою редакційно-видавничої ради Чернівецького державного університету імені Юрія Федьковича
Укладачі: Сопронюк Федір Олексійович, доктор фізико-математичних наук, доцент;
Гайдайчук Ігор Васильович, кандидат фізико-математичних наук, асистент
Літературний редактор: Лупул О.В.
Вступ
Запропоновані методичні вказівки і завдання до лабораторних робіт відповідають курсу “Теорія керування”, який читається для студентів третього курсу спеціальностей “Інформатика” і “Прикладна математика”. Вони покликані допомогти студентам денної та заочної форм навчання більш глибоко засвоїти лекційний матеріал і навчитися застосовувати набуті знання для дослідження та керування конкретними об’єктами, технологічними процесами.
Структура та зміст даної розробки відповідають вимогам “Освітньо-професійної програми вищої освіти України”. До її складу увійшли такі теми:
Передаточні функції ланок лінійних систем керування. Цифрові регулятори.
Дослідження керовності механічних коливних систем.
Модальні регулятори та їх реалізація.
Керування дискретними лінійними системами.
Оптимальне керування. Принцип максимуму Понтрягіна.
Вказані теми охоплюють майже весь лекційний матеріал, передбачений програмою для вищих навчальних закладів. До кожної з них наведені відповідні теоретичні обгрунтування, деякі ілюструються розв’язаннями типових прикладів, запропоновані варіанти завдань для самостійної роботи і перерахована допоміжна література.
Лабораторна робота № 1 Передаточні функції ланок лінійних систем регулювання. Цифрові регулятори
Література: [1, с. 124-141], [3, с. 41-43].
Мета роботи: Вивчити теорію з проблем регулювання в системах керування та розробити алгоритми побудови цифрових пропорційно-інтегрально-диференціальних (ПІД) і адаптивних регуляторів для забезпечення необхідного режиму функціонування керованої системи, якщо невідома її математична модель.
Зміст роботи: Реалізувати однією з мов програмування алгоритм керування об’єктом за допомогою ПІД чи адаптивного регулятора.
Методичні вказівки Нехай структурна схема системи керування має вигляд
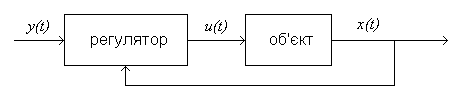
де
– бажана траєкторія руху об’єкта,
– реальна траєкторія руху об’єкта,
– керування, яке розраховується
регулятором і подається на вхід об’єкта.
Точний
вигляд рівняння, що описує реакцію
об’єкта
на вхідне керування, є наперед невідомим,
але вважається, що в будь-який момент
часу
можна вимірювати значення стану об’єкта
.
Цифровий регулятор може бути або
пропорційно-інтегрально-диференціальним
(ПІД) регулятором, або адаптивним.
Керування за допомогою ПІД регулятора розраховується за формулою
,
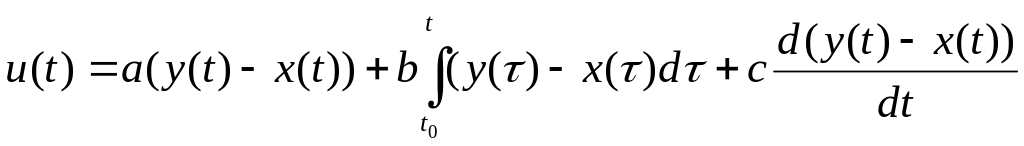де
коефіцієнти
,
,
– параметри регулятора,
–
початкове
значення параметра
,
з якого починається керування об’єктом.
Якщо
використовується адаптивний регулятор,
то значення стану об’єкта
вимірюються в певні моменти
часу
:
,
,
...
.
Позначимо одержані значення так:
...
Припустимо,
що стан об’єкта
при
можна визначити за формулою
,
(1.1)
де
,
–
параметри адаптивного регулятора;
,
...
– керування, які подаються на вхід
об’єкта
при таких значеннях параметра
:
,
...
;
,
– невідомі коефіцієнти, які потрібно
знайти.
Для
забезпечення функціонування системи
керування з адаптивним регулятором
необхідно задати значення станів об’єкта
та параметрів керування
,
а також коефіцієнти
,
,
які пропонується вибирати довільно на
нульовій ітерації, але так, щоб
.
На подальших ітераціях робота адаптивного регулятора складається із двох таких фаз:
фаза самоналагоджування. На кожній ітерації з номером
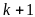для обчислення нових значень коефіцієнтів
,
розв’язується
задача знаходження мінімуму функції
де
– параметр налагодження адаптивного
регулятора.
Якщо для мінімізації функції
використати градієнтну процедуру, то
обчислення нових значень коефіцієнтів
здійснюється за такими рекурентними
формулами:
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
фаза обчислення керування. Для цього в (1.1) замість
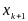потрібно підставити значення
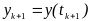і розрахувати
за формулою
.
Завдання для самостійної роботи
Зобразити
на екрані комп’ютера
графік траєкторії
та стану системи керування
,
якщо керування здійснюється за допомогою
ПІД або адаптивного регулятора і
математична модель об’єкта
керування задається передаточною
функцією
.
Це означає, що залежність стану об’єкта
від керування
при нульових початкових умовах (
,
для
)
описується лінійним диференціальним
рівнянням другого порядку зі сталими
коефіцієнтами
.
№ п/п |
Тип регуля-тора |
Передаточна функція |
Параметри |
Бажана траєкторія y(t) |
1 |
ПІД |
|
a=0.5, b=0.3, c=0.2 |
5 |
2 |
Адаптив-ний |
|
n=4, m=1, r=100 |
5 |
3 |
ПІД |
|
a=0.3, b=0.3, c=0.2 |
Sin(0.1t) |
4 |
Адаптив-ний |
|
n=4, m=1, r=100 |
sin(0.1t) |
5 |
ПІД |
|
a=0.5, b=0.2, c=0.1 |
Cos(0.1t) |
6 |
Адаптив-ний |
|
n=5, m=2, r=100 |
Cos(0.1t) |
7 |
ПІД |
|
a=0.5, b=0.3, c=0.2 |
5+0.1cos(0.1t) |
8 |
Адаптив-ний |
|
n=3, m=1, r=100 |
5+0.1cos(0.1t) |
9 |
ПІД |
|
a=0.6, b=0.3, c=0.1 |
sin(0.1t) |
10 |
Адаптив-ний |
|
n=3, m=1, r=100 |
sin(0.1t) |
11 |
ПІД |
|
a=0.4, b=0.4, c=0.1 |
7+0.1sin(0.1t) |
12 |
Адаптив-ний |
|
n=5, m=1, r=100 |
7+0.1sin(0.1t) |
13 |
ПІД |
|
a=0.3, b=0.5, c=0.1 |
Arctg(t) |
14 |
Адаптив-ний |
|
n=4, m=2, r=100 |
Arctg(t) |
15 |
ПІД |
|
a=0.6, b=0.3, c=0.1 |
5 – exp(-t) |
16 |
Адаптив-ний |
|
n=5, m=1, r=100 |
5 – exp(-t) |
17 |
ПІД |
|
a=0.5, b=0.3, c=0.1 |
sin(0.2t) |
18 |
Адаптив-ний |
|
n=4, m=2, r=100 |
sin(0.2t) |
19
|
ПІД |
|
a=0.3, b=0.6, c=0.1 |
cos(0.2t) |
20 |
Адаптив-ний |
|
n=6, m=1, r=100 |
cos(0.2t) |
21 |
ПІД |
|
a=0.2, b=0.8, c=0 |
5 |
22 |
Адаптив-ний |
|
n=5, m=2, r=100 |
5 |
23 |
ПІД |
|
a=0.3, b=0.6, c=0 |
Arctg(t) |
24 |
Адаптив-ний |
|
n=4, m=3, r=100 |
arctg(t) |
25 |
ПІД |
|
a=0.4, b=0.5, c=0.1 |
sin(0.2t) |
26 |
Адаптив-ний |
|
n=4, m=2, r=100 |
sin(0.2t) |
27 |
ПІД |
|
a=0.5, b=0.5, c=0 |
|
28 |
Адаптив-ний |
|
n=5, m=1, r=100 |
|
