Тема Перестановок и подстановок.
Перестановкой
степени н
называют любую упорядоченную запись
натуральных чисел(1,2,…н) в строку, одно
за другим. Sn-
группа всех возможных перестановок в
степени n.
Теорема.
Существует
n!
Различных перестановок в степени
n
Перестановки
образуют беспорядок, если 2 числа образуют
инверсию, если большее число находится
левее меньшего. В противном случае
порядок.
Перестановка четная, если
общее число инверсий четное.
Теорема.
Транспозиция- преобразования перестановки,
при котором 2 элемента меняются местами,
четность перестановки меняется на
противоположную.
подстановкой
n-й
степени называется любое отображение
множества натуральных чисел самого на
себя. Существует n!
подстановок в степени n.
Перестановка
четная, если общее кол-во инверсий обеих
строк четное.
Симметрическая группа
подстановок- множество х, называется
группа всех перестановок х, (т.е. биекцией
х--х),
относительно операции композиции.
5.Определители.
Определитель(детерминант) матрицы –
сумма n!
слагаемых, каждое из которых представляет
собой произведение n-элементов
матрицы, взятых по одному из каждой
строки и каждого столбца. При этом
слагаемое берется со знаком +, если
индексы его сомножителей образуют
четную перестановку. Минор матрицы А -
определитель такой квадратно й матрицы
Б, порядка к,который называется также
порядком этого минора, элемента которой
стоят в матрице А на пересечении строк
с номерами a1,a2…ak,
и столбцов с номерами b1,b2,bk.
Транспонированная
матрица- А
в степени Т полученная из исходной
матрицы А, заменой строк на столбцы.
Вырожденные матрицы- называют квадратную
матрицу, определитель которой равен
нулю. Алгебраическим
дополнением
элемента аij,
матрицы А называется число Аij,
равно -1 в степени i+j*Mij.
Где М и j
дополнительный минор определитель
матрицы, получающийся из исходной
матрицы А,путем вычеркивания i-ой
строки и j-го
столбца. Обратная
матрица. Такая
матрица А в степени -1, при умножении на
которую исходная матрица А дает в
результате
единичную матрицу Е.
2.2Любая транспозиция элементов меняет четность перестановки.
Доказательство.
Утверждение теоремы представляется вполне очевидным в случае транспозиции соседних элементов, поскольку взаимная перестановка элементов ij и ij+1 приводит к появлению или исчезновению инверсии между ними.
Транспозицию элементов ij и ij+k можно рассматривать как результат k последовательных транспозиций элемента ij с соседними элементами, расположенными справа от ij , и последующих k - 1 транспозиций элемента ij+k с соседними элементами, расположенными слева от ij+k :
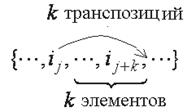
Полное число транспозиций k + (k + 1) = 2 k + 1 является нечетным числом, что означает изменение четности перестановки.
2.3 Существует n! различных перестановок множества S = {1, 2, ..., n}.
Доказательство.
В произвольной перестановке множества S в первой позиции может располагаться любое из первых n натуральных чисел.
Для каждого из этих n вариантов во вторую позицию можно поместить любое из оставшихся (n -1) чисел, в третью – любое из оставшихся (n - 2) чисел и так далее. Последняя n-ая позиция может быть замещена единственным оставшимся элементом.
Таким образом, общее число различных перестановок множества S равно n(n – 1)(n – 2)...1 = n! .
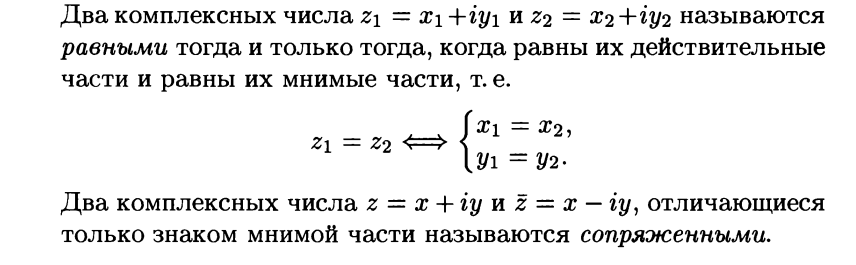Комплексные
числа.
Корни из единицы. Это комплексные корни многочлена х в степени n, -1(n>=1). другими словами, это комплексные числа N-я степень которых равна единице.
Два комплексных числа a + b·i и a - b·i называются сопряженными. Сопряженные комплексные числа в сумме дают действительное число
4 тема Алгебра многочленов от одной неизвестной. Фактор группы и фактор кольца
Теорема Виета
Для начала сформулируем саму теорему: Пусть у нас есть приведённое квадратное уравнение вида x^2+b*x + c = 0. Допустим, это уравнение содержит корни x1 и x2. Тогда по теореме следующие утверждения допустимы:
1) Сумма корней x1 и x2 будет равняться отрицательному значению коэффициента b.
X1+X2 = - b ;
2) Произведение этих самых корней будет давать нам коэффициент c .
X1*X2 = c ;