Шкала профессионального престижа (сокращенный вариант)263

Вид занятий	Баллы	Вид занятий	Баллы
Физик	82	Машинистка	41
Профессор колледжа	78	Водопроводчик	41
Судья	76	Фермер	41
Адвокат	76	Ювелир	37
Врач	74	Часовщик	37
Дантист	74	Стюардесса	36
Банкир	72	Механик	35
Летчик	70	Булочник	34
Министр	69	Сапожник	33
Гражданский инженер	68	Бульдозерист	33
Социолог	66	Водитель грузовика	32
Политолог	66	Кассир	31
Математик	65	Продавец	29
Школьный учитель	63	Мясник	28
Бухгалтер	57	Домработница	25
Библиотекарь	55	Железнодорожник	24
Специалист по компьютерам	51	Газовщик	22
Брокер	51	Таксист	22
Репортер	51	Официант	20
Менеджер в офисе	50	Наемный работник на ферме	18
Офицер полиции	48	Горничная	18
Музыкант	46	Сантехник	17
Секретарша	46	Дворник	17
Пожарный	44	Чистильщик обуви	9
Почтовый служащий	43

В социологии общественного мнения часто используется таблица сопряженности – таблица, содержащая частоты совместного появления значения двух признаков, измеренных в данной совокупности единиц анализа. Строки таблицы сопряженности соответствуют значениям одного из признаков, а столбцы – значениям другого. Частота, стоящая на пересечении определенной строки и определенного столбца, представляет собой число респондентов, имеющих определенное значение по одному признаку и определенное значение по другому признаку. Наряду с частотами, в расположенных на пересечении строк и столбцов клетках часто располагаются относительные частоты (обычно приводимые в виде процентов). Наряду с относительными и абсолютными частотами в таблицах сопряженности приводятся также суммарные частоты по отдельным значениям признаков, а также другая вспомогательная информация. Основное назначение таблицы сопряженности – компактное и удобное для обозрения представление исходной информации в целях выявления связей между признаками. Надо отметить, что таблица сопряженности представляет основной материал анализа, полученный в результате обработки данных.

В ходе интерпретации социологической информации часто приходится прибегать к наглядному изображению статистических величин не только в виде таблиц, но и в виде графики. При этом используются графики разного вида. Строятся графики в прямоугольной системе координат, в которой на одной оси отмечается общая численность (доля, в процентах) респондентов по группам, а на другой оси – значения (порядок) признака. Графическое изображение полученного распределения результатов исследования дает возможность почти сразу определить изучаемую структуру, уловить структурные сдвиги и выявить тенденции изменений.

По итогам массовых опросов часто составляют таблицы с процентным распределением полученных ответов. Для получения показателя, выраженного в процентах (%), число элементов, обладающих определенной спецификой, делится на сумму всех элементов данной категории и умножается на 100. Процентование широко используется при относительных сравнениях («во столько раз…», «в n-ой степени…» и др.).

Одним из самых распространенных графических отображений распределений является полигон, когда величины признака откладываются на оси абсцисс, а частоты или относительные частоты – на оси ординат. Полигон преимущественно используется для графического отображения дискретных рядов.

Другим распространенным видом обобщения является гистограмма («гисто» – клетка) – графическое изображение интервального ряда. В отличие от полигона, здесь отображаются не дискретные, а непрерывные ряды. Здесь на оси абсцисс откладываются границы интервалов, на которых строятся прямоугольники с высотой, пропорциональной плотности распределения соответствующих интервалов.

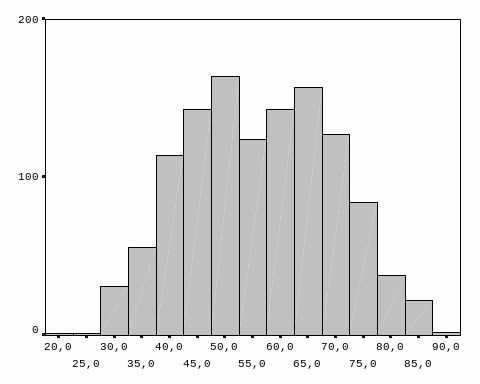
Кумулята – то же, что и гистограмма, но здесь каждый столбик накладывается на другой так, что высота последующего является суммой высот столбиков кумуляты. Кумулята округляет индивидуальные значения признака и выглядит как возрастающая ломаная линия. Она позволяет быстро определить удельный вес той или иной совокупности.

Диаграмма – метод представления частотных распределений путем изображения категории в виде полосы равной ширины, длина которой пропорциональна числу или частоте каждой из обозначенных категорий. Диаграмма – это обобщенное название разнообразных графических изображений. Диаграммы используются для отображения информации простым для восприятия способом. Например, широкое применение составления диаграмм нашло в контент-анализе.

Круговая диаграмма (пи-график, пи-диаграмма) – диаграмма, на которой заштриховывается сектор, соответствующий той или иной частоте категории для данной выборки. Круговая диаграмма применяется для интерпретации изменений относительно величин.

Прямоугольная диаграмма – изображение в виде прямоугольников.

Аксонометрическая диаграмма – изображение в виде брусков.

Фигурная диаграмма – разница в распределении признаков иллюстрируется в виде соответствующих фигур, сопровождаемых цифровыми данными.

Надо помнить, что форму представления данных можно избрать любую, лишь бы она способствовала глубокому содержательному анализу полученных данных. В научном исследовании это всегда выявление закономерностей, определение тенденций и т.д., поэтому для облегчения работы с частотными распределениями зачастую используют «статистики», т.е. некоторые числовые функции, описывающие результаты наблюдений. Наибольшее распространение в социологии общественного мнения получили так называемые «меры центральной тенденции» и «меры разброса (изменчивости)».

Данные меры представляют собой различные способы осмысления центральной или средней позиции группы наблюдений, чисел и др. Они указывают на расположение типичного (среднего) значения признака, вокруг которого группируются остальные наблюдения. Среди мер центральной тенденции наиболее распространенными являются мода, медиана и среднее арифметическое. «Мода – это такое значение в совокупности наблюдений, которое встречается чаще всего. Например, если в выборке содержится 60% православных, 30% мусульман и 10% представителей других конфессий, то модальным значением будет «православный».²⁶⁴ Мода рассчитывается там, где используется мера номинального уровня. Определяется поиском повторяющегося значения.

Медиана – значение, занимающее центральное положение, имея множество величин выше или ниже себя. Медиана лучше всего подходит к мерам порядкового уровня, где относительные расстояния между категориями не известны.

Среднее арифметическое (среднее) вычисляется путем суммирования всех индивидуальных значений и деления суммы на общее число случаев или наблюдений. Среднее используется при мерах интервального уровня (кроме случаев, когда имеется ряд предельных значений, искажающих распределение). «Средняя арифметическая есть интегральная, обобщенная величина, позволяющая сравнить между собой не только группы одного ряда распределений, но и сами ряды распределения в том случае, если они строятся по идентичным признакам».²⁶⁵ Среднее число используется для оценки «нормального» уровня показателей, когда можно пренебречь максимальными и минимальными величинами как малозначимыми.

Меры дисперсии – это различные вычисления степени, в которой совокупность индивидуальных величин (наблюдений, чисел и др.) группируется вокруг центральной точки. Выделяют шесть мер дисперсии. Размах – самая простая мера, касающаяся фактического распространения величин и равная разности между максимальной и минимальной величинами. Средняя дисперсия – мера отклонения совокупности величин от средней, которая используется только с мерами интервального уровня. Ее вычисляют возведением в квадрат среднего арифметического отклонения индивидуальных величин от их средней. Низкое значение средней дисперсии является признаком большой степени однородности величин, а высокая – низкой степени. Стандартное квадратическое отклонение – квадратный корень средней дисперсии. Стандартная ошибка – оценка степени, в которой средняя данной совокупности величин, извлеченных из выборки, отклоняется от истинной средней всей совокупности. Асимметричное отклонение определяет степень отклонения влево или вправо совокупности мер от симметрии кривой нормального распределения. Куртозис показывает степень, в которой «кривая» совокупности наблюдений является более рельефной или более слабой, чем нормальное распределение, чей куртозис равен нулю.²⁶⁶

ПР-службы, как правило, сами не занимаются массовыми опросами, а заказывают проведение соответствующих социологических исследований различным фондам, научно-исследовательским организациям и т.д. Вследствие этого всегда возникает вопрос о достоверности представляемых в отчетах аналитических данных. Национальный совет по опросам общественного мнения США предлагает оценивать степень полезности результатов проведенных опросов следующим образом:

1. Кто проводит опрос? Надежная фирма не скрывает свое авторство и охотно предоставляет информацию, поэтому любой «безымянный» опрос должен вызывать сомнения в его достоверности и научности.

2. Кто оплачивал опрос, и с какой целью? Кто-то всегда заинтересован в результатах опроса. Выявление заказчика опроса и понимание его цели заставляет с большим вниманием (и даже подозрением) отнестись к методологии проведения исследования.

3. Сколько человек было проинтервьюировано? Чем больше людей опрошено, тем меньше вероятность ошибки.

4. Как были выбраны люди для интервью? В научных опросах используется специальная методология отбора респондентов и формирования случайной выборки.

5. Какие критерии заложены в основу формирования выборки: место жительства, этническая принадлежность, профессия, политические убеждения? Телефонные опросы отражают только мнение семей, имеющих телефон. Мнение какого-либо сегмента общественности может существенно отличаться от мнения всего населения в целом. Необходимо знать, из группы населения были выбраны респонденты. Так, во время предвыборных опросов решающим моментом является определение мнения целевой (реально голосующей) группы, а не населения в целом.

6. Основываются ли выводы на ответах опрошенных? Один из способов манипуляции результатами опросов – выдавать мнение отдельной группы за мнение всего населения в целом.

7. Кого следовало опросить, кто не был опрошен? Необходимо знать, сколько людей отказалось отвечать или со сколькими людьми из выборки вообще не удалось вступить в контакт.

8. Когда проводился опрос? Самые разные события могут повлиять на результаты опроса или же мгновенно превратить абсолютно точные и научные выводы в устаревшие.

9. Как проводились интервью? Надо помнить, что, например, опросы в местах большого скопления людей (торговых центрах и т.д.) представляют несомненный интерес для заказчика, решающего свою конкретную задачу, однако не могут отражать мнение всего населения.

10. Не является ли опрос результатом добровольных звонков или писем респондентов? В таком случае выборка абсолютна нерепрезентативна (респонденты могут быть ангажированы, а один респондент может дать сотню ответов).

11. Какова ошибка прогноза? Значение отклонения от прогноза особенно важно в случаях, когда определяется рейтинг нескольких лиц (при политических опросах), компаний, товаров или услуг.

12. Какие еще ошибки могут исказить результаты? Источником ошибок может быть некорректная постановка вопроса, плохая подготовка интервьюеров и т.д.

13. Какие вопросы задавались? Результаты исследований (особенно по деликатным вопросам) сильно зависят от постановки вопросов.

14. В каком порядке задавались вопросы? Важно понять, не находятся ли в анкете перед основным вопросом те, которые могут оказать психологическое воздействие на респондента. Например, если перед вопросом об оценке того или иного политического лидера стоит вопрос о состоянии экономики, то на ответе обязательно скажется оценка экономической ситуации респондентом.

15. Какие еще вопросы проводились по этой теме? Совпали ли результаты? Если нет, то почему? Сравнение с другими аналогичными исследованиями позволяет проверить достоверность результатов. Например, различие может быть объяснено сопоставлением времени проведения опросов.

16. Опрос закончен, что дальше? Опрос позволяет сделать прогноз. Ни один опрос не даст окончательного решения на будущее. Все течет, все изменяется.

17. Не был ли вопрос лишь завуалированной попыткой сбора средств? Иногда анкеты заканчиваются просьбой внести вклад в какой-либо фонд или присоединиться к какой-либо партии. Это был не опрос.²⁶⁷

Выводы

1. Обработка данных включает в себя: а) редактирование и кодирование информации с целью унификации и формализации полученной в ходе социологического исследования информации; б) создание переменных; в) статистический анализ, при котором выявляются статистические (количественные) зависимости и закономерности, позволяющие сделать некоторые качественные обобщения и выводы.

2. Измерение производится с помощью различных шкал, которым соответствуют различные правила математического анализа данных. В социологических исследованиях применяются, как правило, шкалы трех основных типов: номинальная ранговая (порядковая) и интервальная. Простейшая шкала – номинальная (фиксирует дихотомичный ответ: «да» или «нет» и т.п.). Ранговая шкала зафиксирует более определенное состояние, отражающее ранжированное распределение типа «согласен» – «скорее согласен, чем не согласен» – «не знаю» – «скорее не согласен, чем согласен» – «не согласен». Интервальная шкала более детальна, глубока. Она допускает обстоятельную математическую обработку информации.

3. С точки зрения Г. Осипова и Э. Андреева социологические шкалы различаются прежде всего по трем моментам: природе шкалируемого явления, уровню числового представления, способам получения числового представления. Так, по уровню измерения выделяются шкалы номинальные, порядковые, интервальные, пропорциональные. По методу составления шкалы подразделяются на составляемые с помощью метода суждения (Л. Терстоун), метода суммарных оценок (Л. Лайкерт) и метода шкалограмм (Л. Гуттман).

4. В анализе данных массовых опросов используют методы ранжирования, статистические методы обработки данных и т.д. Сначала производится группировка непрерывных количественных признаков в интервалы. При необходимости строятся ряды распределения данных.

Затем вычисляются проценты, коэффициенты, индексы, основные характеристики распределения рядов данных. Частотные распределения представляются в виде графиков и диаграмм.

При необходимости сопоставления распределение признаков для различных групп респондентов составляют таблицы. Таблицы сопряженности служат для проверки гипотезы о статистической связи между признаками. Обычно гипотезы проверяются по критерию «хи квадрат». Для измерения связи применяют различные коэффициенты.

5. Представленный в виде таблиц, схем, графиков, диаграмм и т.д. материал, подвергается системному анализу со стороны специальной исследовательской группы, после чего готовится соответствующий отчет (публикация в СМИ, научная статья или монография и т.д.).