2. Комитетные методы решения задач распознавания Комитеты

Нас интересует случай, когда теоретико-множественная задача не разрешима. Идея комитетного метода распознавания состоит в использовании нескольких классификаторов, каждый из которых дает свой результат. Далее по какому-либо общему правилу голосования на основе полученных результатов от каждого классификатора выдается итоговый результат.

Определение. Для исходной системы и числа конечное подмножество называется -комитетом в классе , если для всех выполнено неравенство (относительная доля , лежащая в , превосходит ). Если , то -комитет называется просто комитетом.

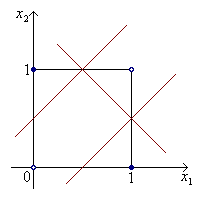
Пример комитета для несовместной системы. Рассмотрим задачу исключающего или. , , , . Пусть а – множество линейных классификаторов. Опишем множество : , , , , . Пусть . Построим комитет :

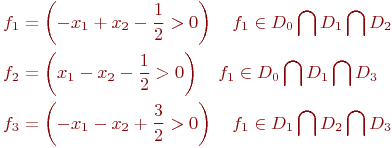
			Класс
	0	0	B(0)	0	0	1
	1	1	B(0)	0	0	0
	0	1	A(1)	1	0-	1
	1	0	A(1)	0	1	1

, , , . .

Следовательно, есть комитет в классе линейных классификаторов.

Определение. Пусть (подмножества, возможно, бесконечные) и – класс функционалов. Набор функционалов называется разделяющим комитетом для множеств и , если

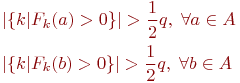
Утверждение. Чтобы набор был разделяющим комитетом для и необходимо, чтобы для каждой пары и нашелся такой , что и .

Доказательство. Если – число функционалов , – число функционалов , то

И, т.к. найдется функционал, обладающий обоими свойствами, утверждение доказано.

Теорема. Пусть ; , . И пусть (нет нулевой точки); , (не коллинеарны). Тогда для таких и существует разделяющий комитет в классе аффинных функционалов: .

Доказательство. Построим комитет из элементов (функционалов):

Для каждого функционала необходимо найти и в – пару, которая определяет функционал , причем , т.е. и , т.е. не ортогонален остальным . Другими словами каждая гиперплоскость должна иметь направляющий вектор, ортогональный своему прецеденту и не ортогональный всем остальным.

Пусть . Выберем следующим образом:

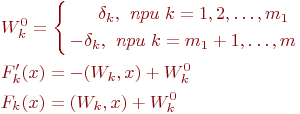
Покажем, что построенное множество функционалов является комитетом для и . Рассмотрим

и правильно классифицируют . Посмотрим, как будет работать каждй такой функционал на остальных :

Т.к. , то знак определяется знаком .

Рассмотрим . и голосуют правильно, т.е. соответствует правильное положение гиперплоскостей. и имеют разные знаки. Следовательно, каждая пара и правильно классифицирует на всех и дает одну правильную классификацию на остальных . Таким образом, количество правильно голосующих за равно .