Задание для самостоятельной работы

Задача 9. Вычислить .

Задача 10. Вычислить .

Задача 11. Вычислить .

Задача 12. Вычислить .

Задача 13. Вычислить .

Задача 14. Найти предел .

Задача 15. Найти предел .

Занятие №8. Исследование функций и построение графиков с помощью производной

Краткая информация о новых учебных элементах

1. Значение функции в точке называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках слева и справа от .

2. Функция может иметь экстремум (максимум или минимум) в тех точках, которые лежат внутри области определения функции и в которых производная равна 0. Такие точки называются критическими.

3. Функция будет иметь экстремум в тех точках, где ее производная меняет свой знак, а сама функция непрерывна.

4. Если в некотором интервале кривая расположена ниже любой своей касательной, то она называется выпуклой вверх, а если она расположена выше любой своей касательной, то называется выпуклой вниз в этом интервале.

5. Направление выпуклости кривой характеризуется знаком второй производной .

Если меняет свой знак при переходе через точку, в которой или не существует, то данная точка является точкой перегиба.

6. Асимптотой кривой называется такая прямая, к которой график функции неограниченно приближается. Если 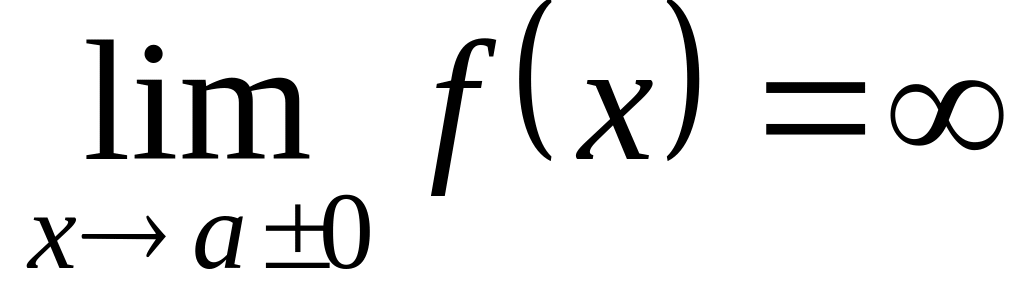, то прямая 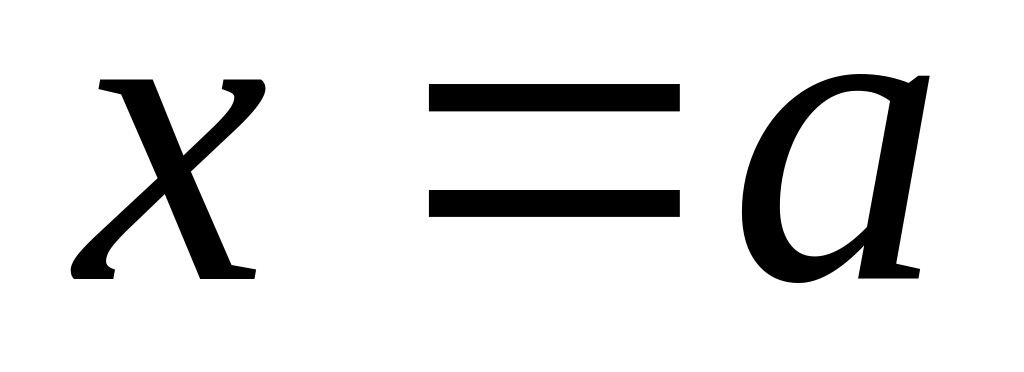называется асимптотой вертикальной. Если существует наклонная асимптота, то ее уравнение имеет вид:

причем , .

Задача 1. Исследовать функцию и построить ее график.

1. Область определения данной функции – все действительные числа, так как функция представляет собой многочлен.

2. Точки пересечения с осями.

Если точка лежит на оси Оу, то .

Если точка лежит на оси Ох, то .

Для решения кубического уравнения

а) рассмотрим делители свободного члена : ; если , то , значит корень данного уравнения.

б) разделим многочлен на двучлен , т.е. :

в) решим квадратное уравнение:

.

Значит, график пересекает ось Ох в точке и касается в т. .

3. Промежутки знакопостоянства функции.

Итак, многочлен, определяющий данную функцию можно разложить на множители: . Определим знак функции в каждом из интервалов:

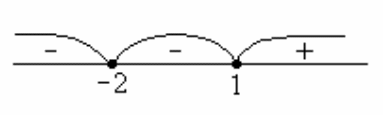
Если , то .

Если , то .

Если , то .

Значит, на график функции располагается ниже оси Ох, а на - выше.

4. Чётность.

Вычислим .

и .

Значит, функция не обладает данными свойствами.

5. Исследование на экстремум.

;

критические точки.

Составим таблицу и определим знак производной в каждом интервале.

				0
	+	0		0	+
		max		min

Найдем значения функции в точках экстремума.

;

.

Изобразим эти точки на графике.

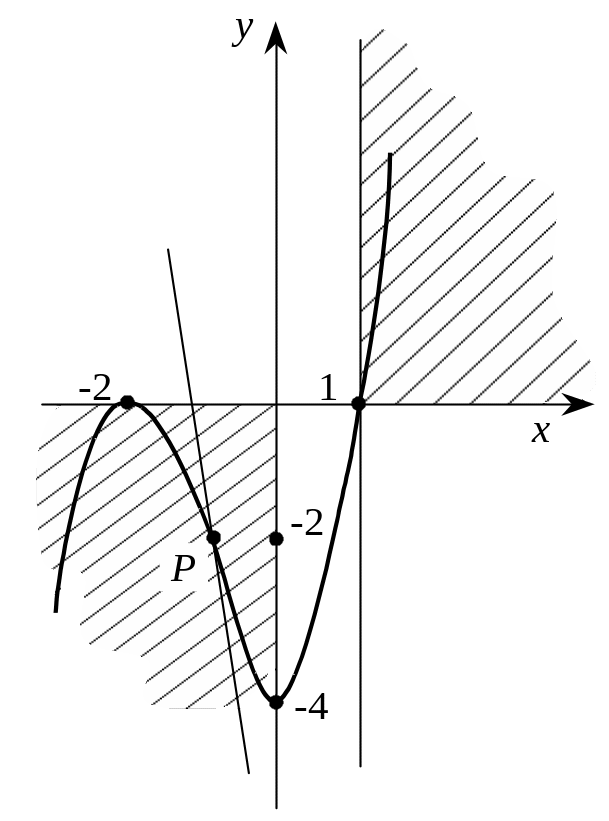
Рис. 5

6. Исследование на перегиб.

, если . При переходе через эту точку меняет знак, т.к. .

Отметим эту точку на графике.

Подставим координаты в уравнение где :

,

значит, касательная имеет уравнение . Построим ее:

х	0
у		0

7. Построение графика (рис. 5).

Для уточнения положения графика найдем координаты некоторых его точек:

х
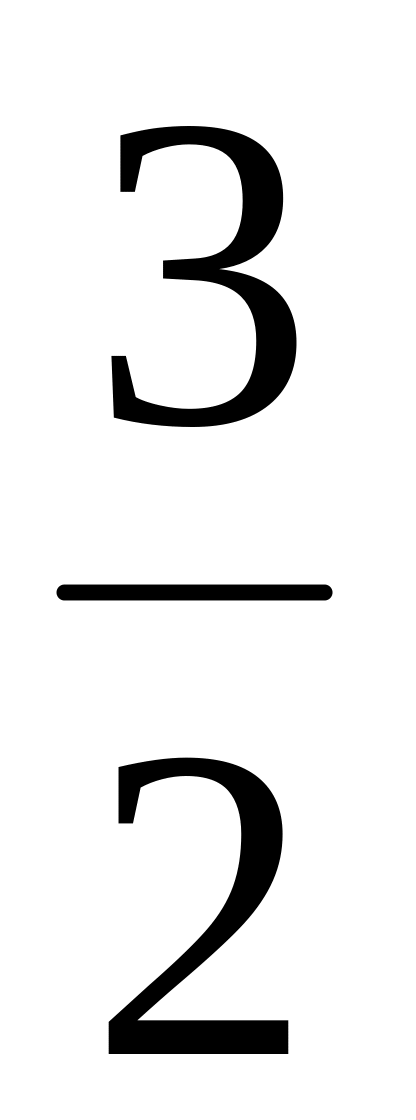
у

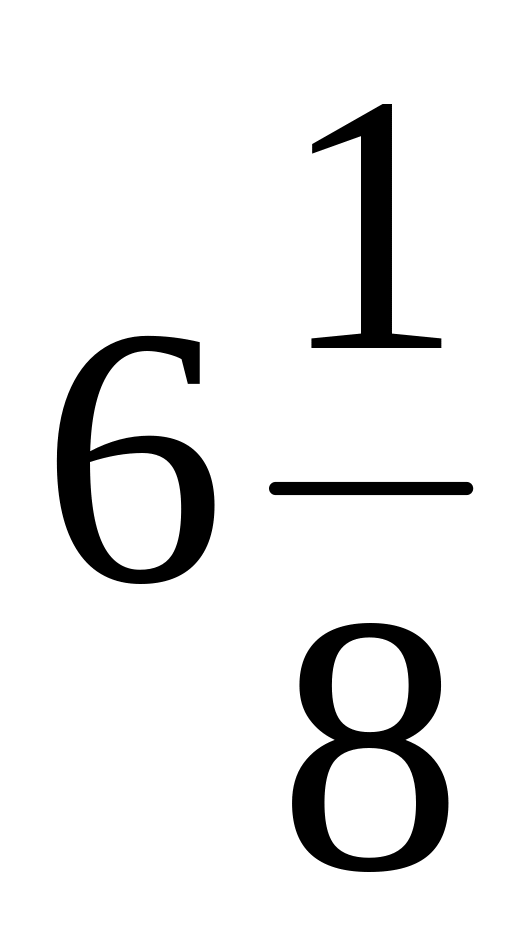
Задача 2. Исследовать функцию и построить ее график:

.

Решение. 1. Область определения функции.

Делить на 0 нельзя, поэтому , , значит вертикальная асимптота.

2. Точки пересечения с осями.

С осью Оу: ,

;

С осью Ох:

.

3. Промежутки знакопостоянства функции:

при

при

при

при .

4. Исследование на экстремум.

.

Экстремума нет, т.к. критическая точка , в которой , не входит в область определения.

5. Исследование на перегиб.

.

При переходе через точку кривая меняет направление выпуклости, но т.к. эта точка является точкой разрыва, значит «перегиба» не существует.

Рис. 6

6. Построение асимптот (наклонных): .

.

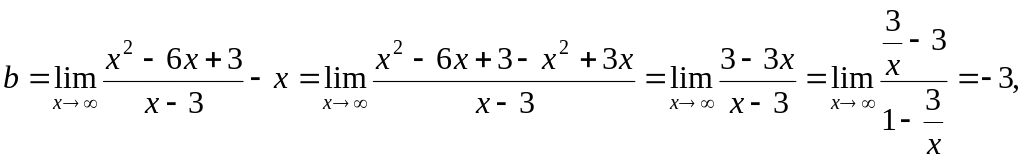
Строим прямую по точкам:

х	0	3
у		0

7. Построение графика (рис. 6).

Для уточнения положения графика найдем значение заданной функции в точках .

х				1	2	4	5	7
у				1	5			2,5

Задача 3. Исследовать функцию и построить ее график:

.

1. Область определения – все действительные числа.

2. Точки пересечения с осями.

С осью Оу:

С осью Ох: .

3. Промежутки знакопостоянства функции.

;

.

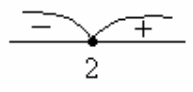
4. Исследование на экстремум.

;

.

х		1
у		min

.

5. Исследование на перегиб.

.

- точка перегиба, т.к. при всех х.

при

при .

. Точка перегиба .

6. Построение асимптот.

.

Следовательно, ось Ох является горизонтальной асимптотой.

7. Для построения графика (рис. 7) вычислим значения функции в некоторых точках:

; .

Рис. 7