Задание для самостоятельной работы Задача 11. Найти от следующих функций:

Задача 12. а) Найти от функции ; б) Найти от функции ; в) Показать, что функция удовлетворяет дифференциальному уравнению .

Задача 13. Найти , если .

Задача 14. Уравнение движения точки на оси Ох есть . Найти скорость и ускорение точки для моментов времени .

Задача 15. Найти производную второго порядка от функции .

Задача 16. Найти производную третьего порядка от функции .

Задача 17. Найти от функций:

Занятие №5. Дифференциал функции

Цель занятия: усвоить новые учебные элементы на уровне знаний и умения применять к решению типовых задач.

Учебные вопросы

1. Нахождение дифференциалов функций.

2. Применение дифференциалов к приближенным вычислениям.

Краткая информация о новых учебных элементах

Пусть функция имеет производную в некоторой точке и аргумент, принимавшей некоторое значение х получил приращение .

Определение. Дифференциалом функции называется главная часть ее приращения, линейная относительно приращения аргумента :

. (1)

Так как дифференциал dx аргумента х равен его приращению, то есть , то дифференциал функции принимает вид:

. (2)

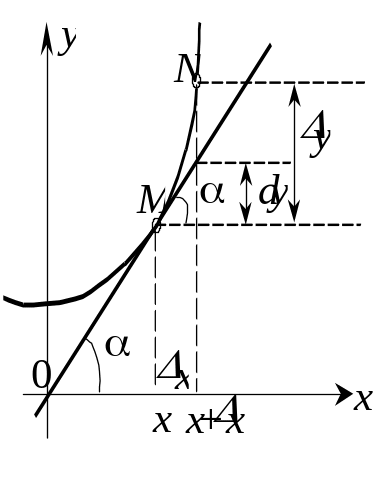
Рис. 4

Геометрически дифференциал представляет собой приращение ординаты касательной к графику функции в точке М (рис. 4).

Основные свойства дифференциала

1. , где .

2. .

3. .

4. .

5. .

6. .

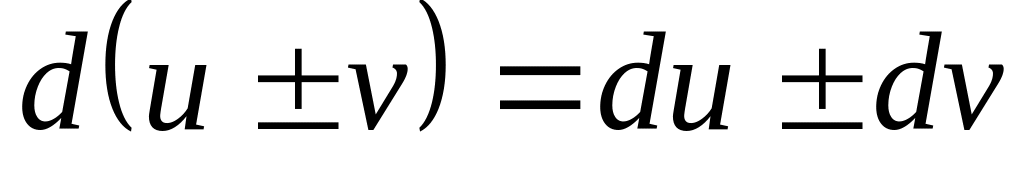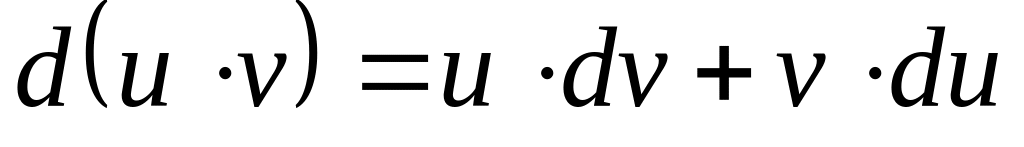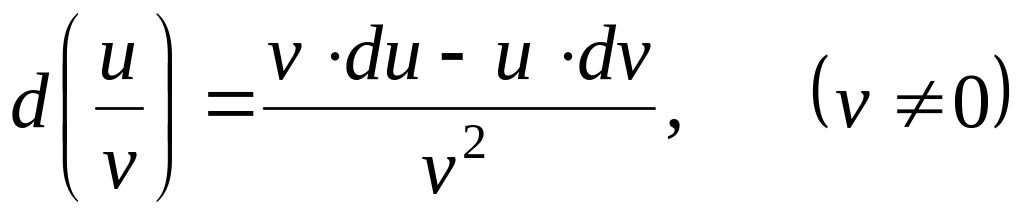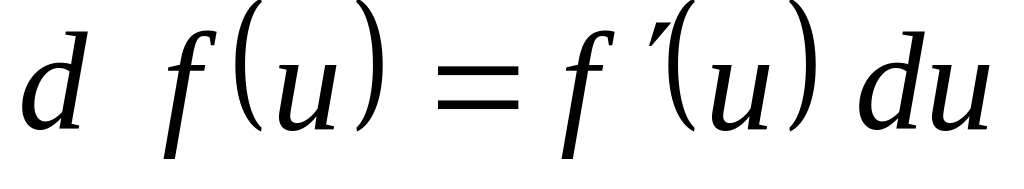Если приращение аргумента мало по абсолютной величине, то

. (3)

Таким образом, дифференциал функции может применяться для приближенных вычислений.

Задача 1. Найти , если .

Решение. Так как , имеем:

.

Задача 2. Найти дифференциал функции .

Решение. Имеем:

.

Задача 3. Найти .

Задача 4. Найти .

Задача 5. Найти дифференциал функции .

Задача 6. Найти , если .

Решение. Имеем:

.

Задача 7. Найти .

Задача 8. Доказать равенства:

1. ;

2. ;

3. .

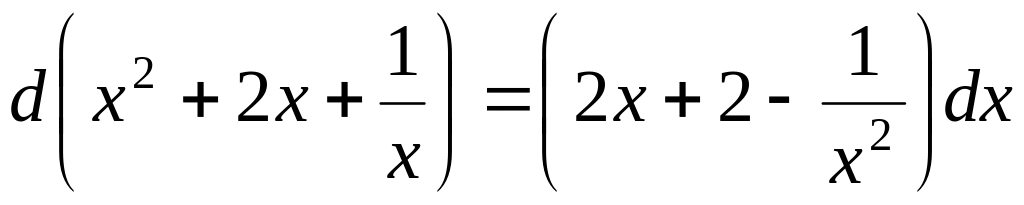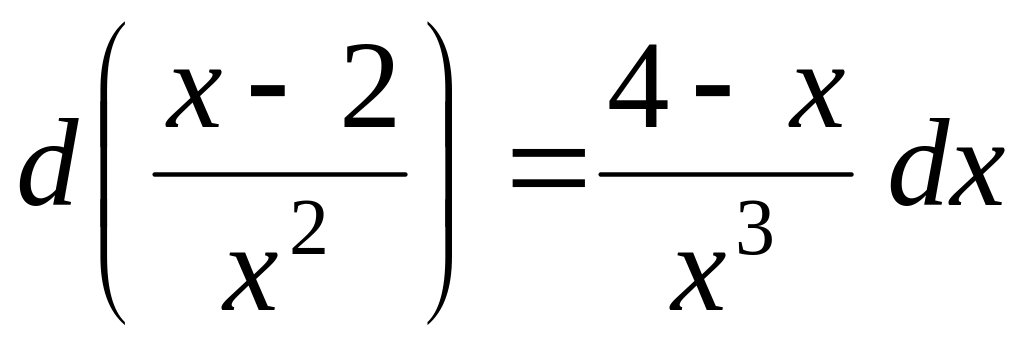Задача 9. Вычислить приближенное значение .

Решение. Рассмотрим функцию . Полагая и применяя формулу

,

получаем:

, или

.

Задача 10. Вычислить приближенно .

Решение. Рассмотрим функцию , полагая и применяя формулу (3), имеем:

, или

.

Задача 11. Вычислить приближенное значение площади круга, радиус которого равен м.

Решение. Воспользуемся формулой , полагая имеем:

.

Следовательно, приближенное значение площади составляет

.

Задание для самостоятельной работы

Задача 12. Найти дифференциалы следующих функций:

.

Задача 13. Вывести приближенную формулу

и найти приближенные значения для .

Задача 14. Найти приближенное значение .

Указание. выразить в радианах, зная, что соответствует радиан.

Задача 15. Найти дифференциалы следующих функций:

.

Задача 16. Найти дифференциал функции , определить и dy и вычислить их при изменении х от 2 до 1,98.

Занятие №6. Подготовка к контрольной работе по теме 2

Цель занятия: закрепить знание учебных элементов и навыки решения типовых задач по теме.

Учебные вопросы

1. Производная сложной функции.

2. Производная функции, заданной параметрически.

3. Вычисление значений производной в точке.

4. Дифференциал функции.

5. Геометрические и механические приложения производной.

Пользуясь таблицей производных и правилом дифференцирования сложной функции, найти производные функций, разобрать решения следующих задач:

Задача 1. .

Решение. Воспользуемся формулой , полагая , . Имеем:

.

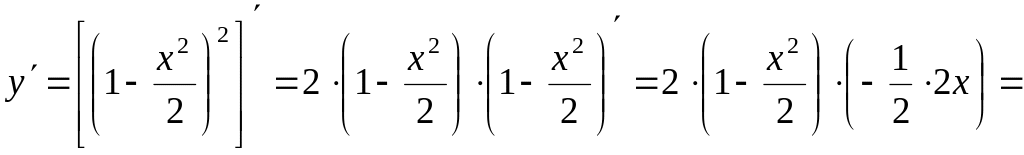
Задача 2. .

Решение.

.

Задача 3. .

Задача 4. .

Задача 5. Разобрать решение задачи: .

Решение. Полагая имеем .

Воспользуемся формулой :

.

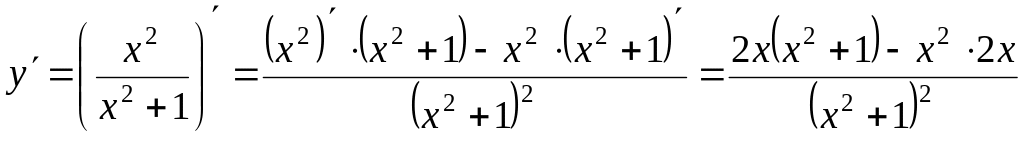
Задача 6. Решить самостоятельно: .

Задача 7. Разобрать решение задачи: .

Решение. Воспользуемся формулой , полагая . Имеем:

.

Задача 8. Решить самостоятельно: .

Задача 9. Разобрать решение задачи. Найти , если .

Решение. Так как , найдем

.

Имеем:

.

Задача 10. Решить самостоятельно: . Найти .

Задача 11. Разобрать решение задачи: . Найти .

Решение. Найдем:

.

.

Задача 12. Решить самостоятельно: . Найти .

Задача 13. Разобрать решение задачи. Найти .

Решение. Воспользуемся формулой дифференциала функции

,

где .

.