
- •Тема 1. Введение в анализ
- •Краткие сведения из теории
- •Задание для студентов
- •Основные теоремы о пределах
- •1. Раскрытие неопределенности вида
- •2. Раскрытие неопределенности вида
- •3. Вычисление значений сложной функции
- •Тема 2. Дифференциальное исчисление функции одной переменной
- •Краткая информация о новых учебных элементах
- •Основные формулы дифференцирования
- •Занятие №1. Задачи, приводящие к понятию производной
- •Итак, исходя из условия задачи, найдем координаты точки касания м : , получим
- •Задание для самостоятельной работы
- •Занятие №2. Производная сложной функции
- •Ход занятия
- •Задание для самостоятельной работы
- •Разобрать решение задач:
- •Занятие №3. Производная сложной функции (продолжение)
- •Ход занятия
- •Вычисление производной функции в данной точке
- •Задание для самостоятельной работы
- •Занятие №4. Дифференцирование функций
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы Задача 11. Найти от следующих функций:
- •Занятие №5. Дифференциал функции
- •Краткая информация о новых учебных элементах
- •Основные свойства дифференциала
- •Задание для самостоятельной работы
- •Занятие №6. Подготовка к контрольной работе по теме 2
- •Решить самостоятельно:
- •Задание для самостоятельной работы
- •Занятие №7. Вычисление пределов с помощью производной
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Для решения кубического уравнения
- •Задание для самостоятельной работы
- •Тема 3. Комплексные числа
- •Краткая информация о новых учебных элементах
- •1. Комплексные числа и их геометрическая интерпретация
- •2. Действия над комплексными числами, заданными алгебраической формой
- •3. Перевод комплексных чисел из алгебраической формы записи в тригонометрическую и показательную и обратно
- •4. Действия над комплексными числами в тригонометрической форме
- •5. Действия над комплексными числами в показательной форме записи
- •Занятие №1. Комплексные числа
- •Задание для самостоятельной работы
- •Занятие №2. Комплексные числа (продолжение)
- •Задание для самостоятельной работы
- •Тема 4. Неопределенный интеграл Введение
- •Свойства неопределенного интеграла
- •Занятие №1. Непосредственное интегрирование функций
- •Ход занятия Краткая информация о новых учебных элементах
- •Геометрическая иллюстрация неопределенного интеграла
- •Задание для самостоятельной работы
- •Занятие №2. Метод замены переменных
- •Краткая информация о новых учебных элементах
- •Задание для студентов
- •Задание для самостоятельной работы
- •Занятие №3. Метод интегрирования по частям
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Занятие №4. Метод интегрирования по частям (продолжение)
- •Учебные вопросы
- •Задание для самостоятельной работы
- •Занятие №5. Интегрирование рациональных дробей
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Занятие №6. Интегрирование рациональных дробей (продолжение)
- •Алгоритм нахождения интеграла методом неопределенных коэффициентов
- •Задача 6. Найти интегралы методом неопределенных коэффициентов:
- •Задание для самостоятельной работы
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Занятие №9. Интегрирование некоторых иррациональных функций
- •Краткая информация о новых учебных элементах
- •Занятие №11. Контрольная работа по теме «Неопределенный интеграл»
- •Образец одного из вариантов
- •Занятие №12. Анализ контрольной работы
- •Задание для самостоятельной работы
- •Тема 5. Определенный интеграл
- •Краткие сведения из теории
- •Основные свойства определенного интеграла
- •1. Несобственные интегралы первого рода
- •2. Несобственные интегралы второго рода
- •Задача 3. Исследовать на сходимость интеграл .
- •1. Площадь плоской фигуры
- •2. Длина дуги плоской кривой
- •3. Площадь поверхности фигуры вращения
- •4. Объем тела
- •Задание для самостоятельной работы
- •Занятие №5. Геометрическое приложение определенного интеграла (продолжение)
- •Задача 11. Найти площадь поверхности фигуры при вращении её вокруг полярной оси.
- •Задание для самостоятельной работы
- •Занятие №6. Механическое приложение определенного интеграла
- •Краткая информация о новых учебных элементах
- •Задача 5. Определить величину давления морской воды на вертикальный круг радиуса м, центр которого погружен в воду на глубину м. Плотность морской воды кг/ .
- •Задача 10. Найти координаты масс однородной дуги окружности радиусом r с центральным углом . Задание для самостоятельной работы
1. Площадь плоской фигуры
Площадь фигуры, ограниченной графиком непрерывной функции
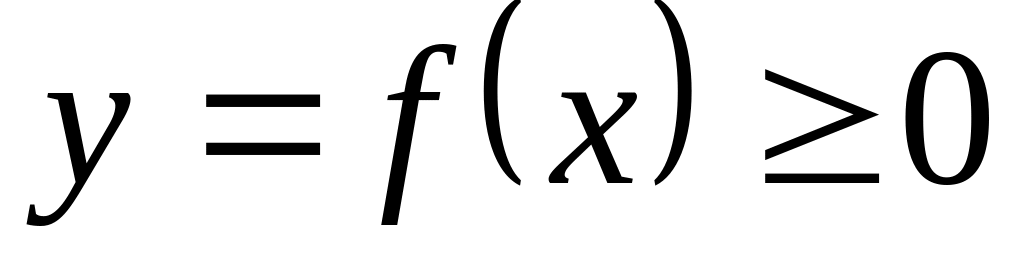 ,
двумя прямыми
,
двумя прямыми
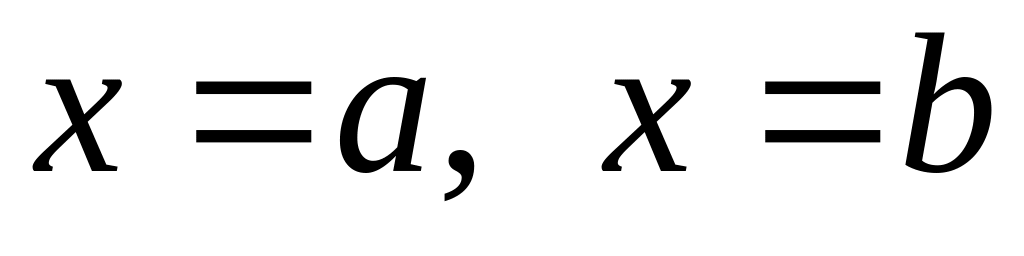 и осью Ох
(рис. 4)
определяется по формуле:
и осью Ох
(рис. 4)
определяется по формуле:
![]() . (1)
. (1)

Рис. 4
Площадь
фигуры, ограниченной графиком непрерывной
функции
![]() ,
двумя прямыми
и осью Ох
(рис. 5)
находится по формуле:
,
двумя прямыми
и осью Ох
(рис. 5)
находится по формуле:
![]() . (2)
. (2)

Рис. 5
Площадь фигуры, ограниченной графиком непрерывной функции , когда функция меняет знак на отрезке , двумя прямыми и осью Ох (рис. 6) вычисляется с помощью формулы:
![]() , (3)
, (3)
где с и d – точки пересечения графика функции с осью Ох.

Рис. 6
Площадь
фигуры, ограниченной графиками непрерывных
функций
![]() и
и
![]() ,
где
,
где
![]() ,
двумя прямыми
и осью Ох
(рис. 7)
определяется по формуле:
,
двумя прямыми
и осью Ох
(рис. 7)
определяется по формуле:
![]() . (4)
. (4)
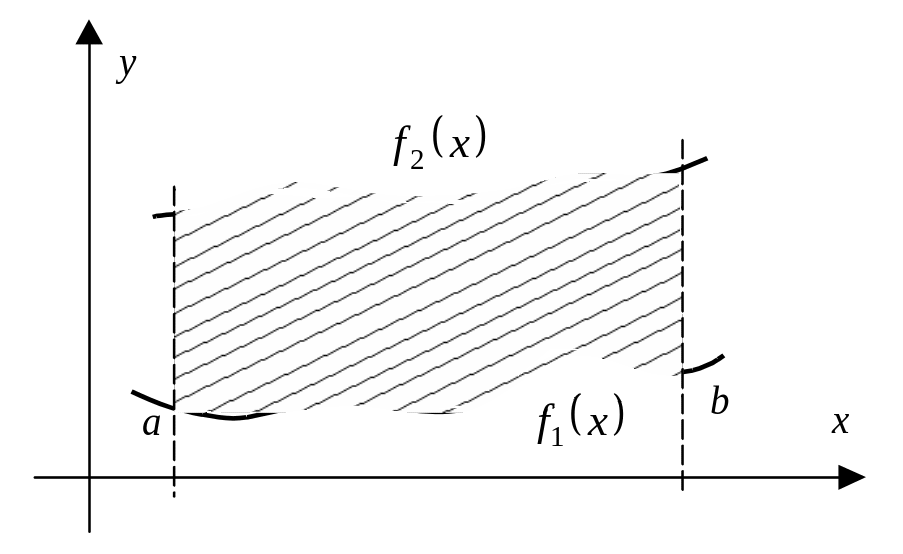
Рис. 7
2. Площадь
фигуры, ограниченной графиком функции,
заданной параметрически
![]() ,
двумя прямыми
и осью Ох
(рис. 8)
находится с помощью формулы:
,
двумя прямыми
и осью Ох
(рис. 8)
находится с помощью формулы:
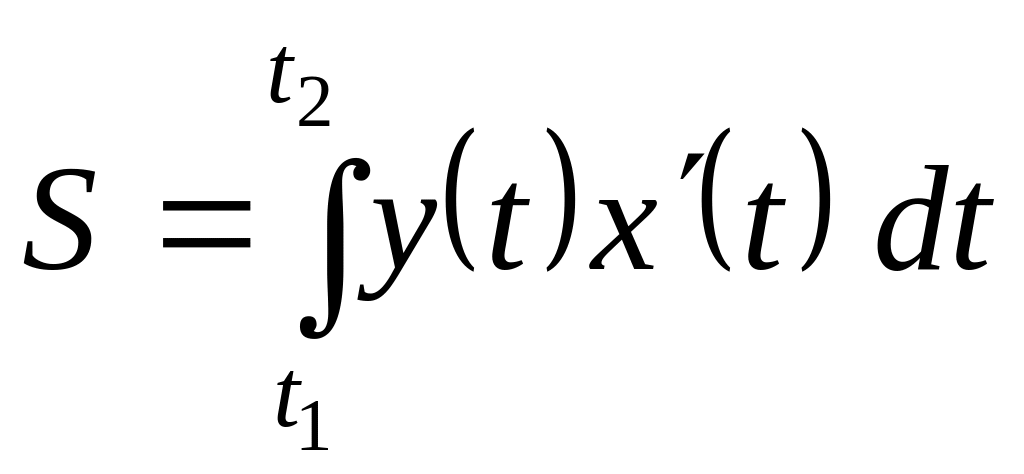 , (5)
, (5)
где
![]() ,
,
![]() (обход по часовой стрелке от
(обход по часовой стрелке от
![]() до
до
![]() ).
).

Рис. 8
3. Площадь
фигуры, ограниченной графиком непрерывной
функции
![]() и двумя лучами
и двумя лучами
![]() ,
где
,
где
![]() и r
– полярные координаты,
и r
– полярные координаты,
![]() (рис. 9):
(рис. 9):
![]() . (6)
. (6)
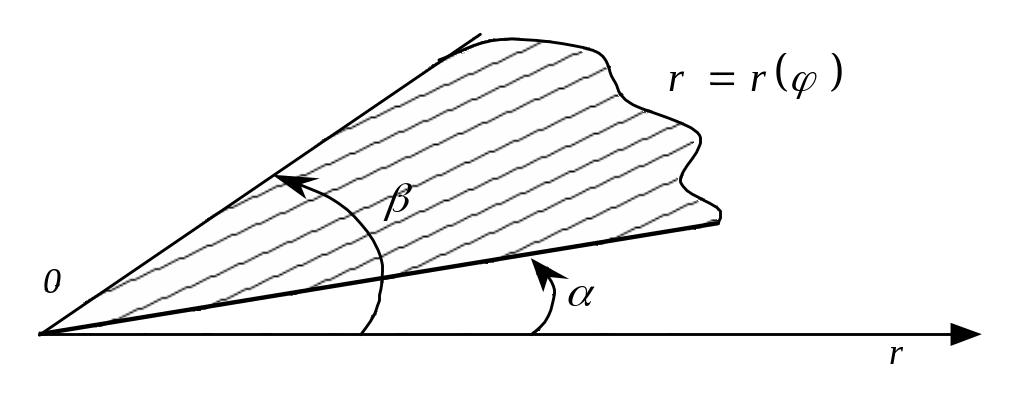
Рис. 9
2. Длина дуги плоской кривой
Плоская кривая задана уравнением , а и b – абсциссы концов дуги, тогда длина дуги кривой (рис. 10) определяется по формуле:
![]() . (7)
. (7)
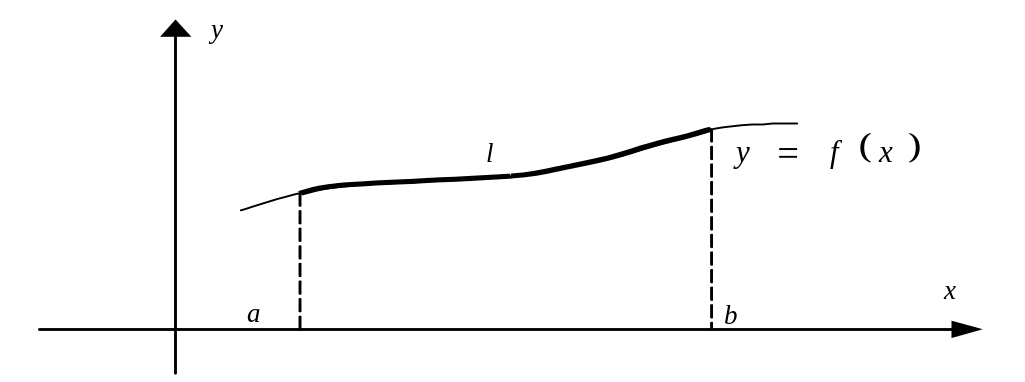
Рис. 10
Плоская кривая задана параметрически

 ,
тогда длина дуги кривой вычисляется
по формуле:
,
тогда длина дуги кривой вычисляется
по формуле:
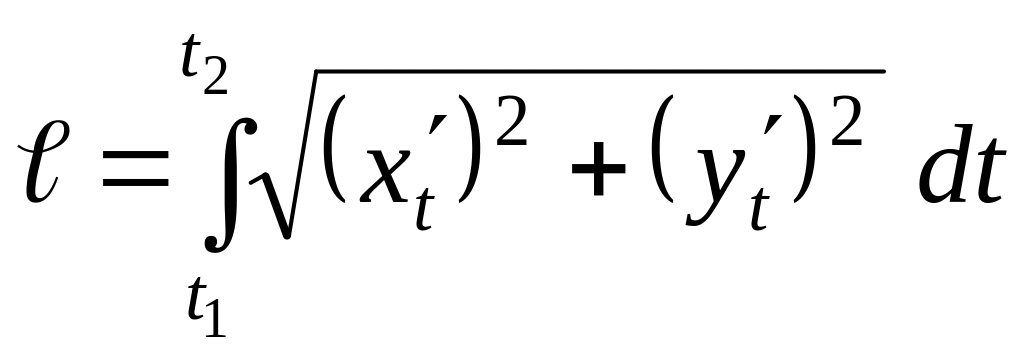 . (8)
. (8)
Плоская кривая задана уравнением в полярных координатах
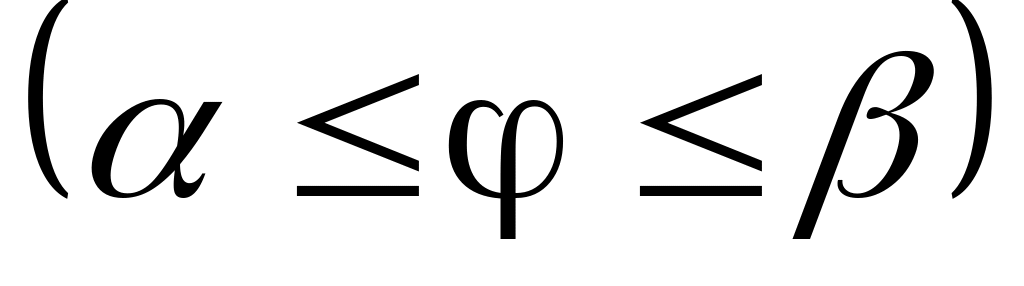 ,
тогда длина дуги кривой определяется
формулой:
,
тогда длина дуги кривой определяется
формулой:
![]() . (9)
. (9)
3. Площадь поверхности фигуры вращения
Площадь поверхности, образованная вращением вокруг оси Ох кривой ,
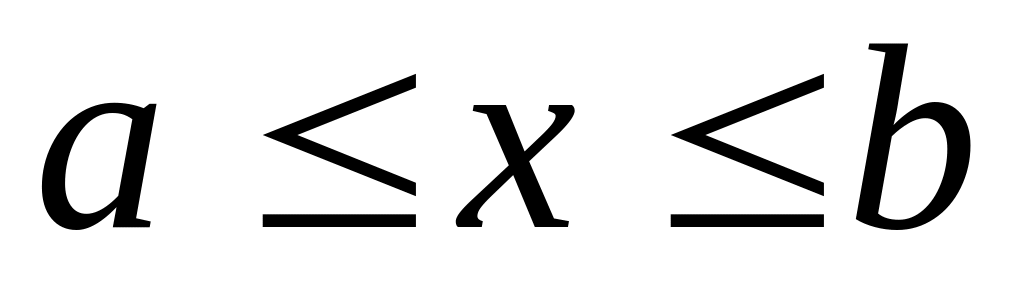 вычисляется по формуле:
вычисляется по формуле:
![]() . (10)
. (10)
Площадь поверхности, образованная вращением вокруг оси Ох кривой, заданной параметрически ,
 ,
находится с помощью формулы:
,
находится с помощью формулы:
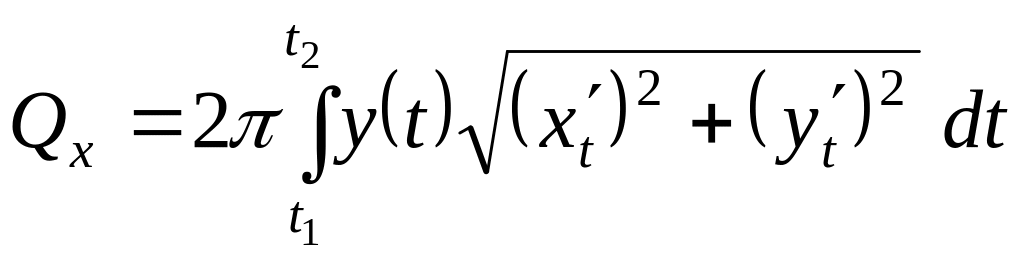 . (11)
. (11)
3. Площадь поверхности, образованная вращением вокруг полярной оси кривой, заданной в полярных координатах , определяется формулой:
![]() . (12)
. (12)
4. Площадь поверхности, образованная вращением вокруг произвольной оси произвольной кривой, вычисляется по формуле:
![]() , (13)
, (13)
где R – расстояние от точки кривой до оси вращения;
![]() дифференциал
дуги;
дифференциал
дуги;
А
и В
– пределы интегрирования, соответствующие
концам дуги (![]() должны быть выражены через переменную
интегрирования).
должны быть выражены через переменную
интегрирования).
4. Объем тела
1. Если
площадь
![]() сечения тела плоскостью, перпендикулярной
оси Ох,
является непрерывной функцией на отрезке
,
то объем тела (рис. 11) находится по
формуле:
сечения тела плоскостью, перпендикулярной
оси Ох,
является непрерывной функцией на отрезке
,
то объем тела (рис. 11) находится по
формуле:
![]() . (14)
. (14)
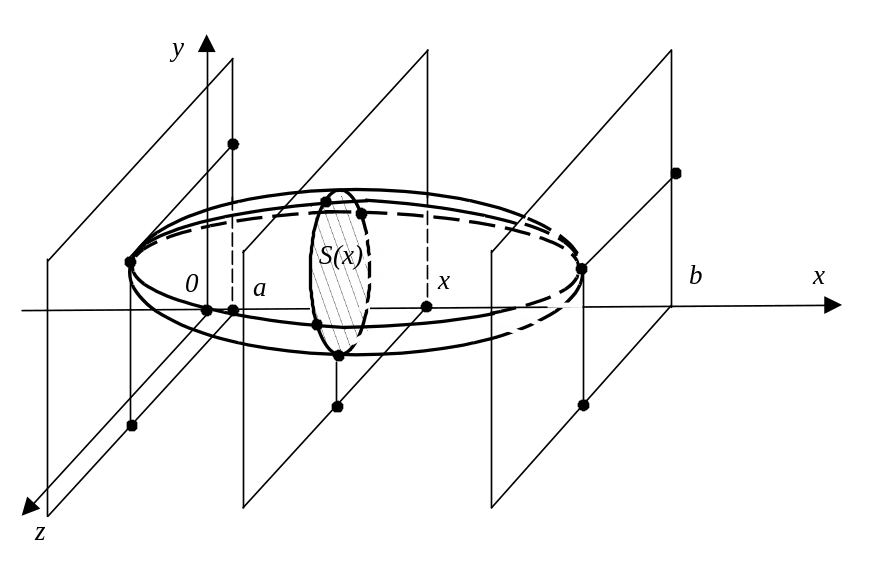
Рис. 11
2. Объем тела вращения криволинейной трапеции, ограниченной графиком функции , прямыми и , вокруг оси Ох находится по формуле:
![]() ; (15)
; (15)
вокруг оси Оу:
![]() . (16)
. (16)
3. Объем
тела вращения криволинейного сектора,
ограниченного кривой, заданной в полярных
координатах
и лучами
![]() и
и
![]() вокруг полярной оси, вычисляется с
помощью формулы:
вокруг полярной оси, вычисляется с
помощью формулы:
![]() . (17)
. (17)
Задача
1. Найти
площадь фигуры, ограниченной графиком
функции
![]() ,
прямыми
,
прямыми
![]() и осью Ох
(рис. 12).
и осью Ох
(рис. 12).
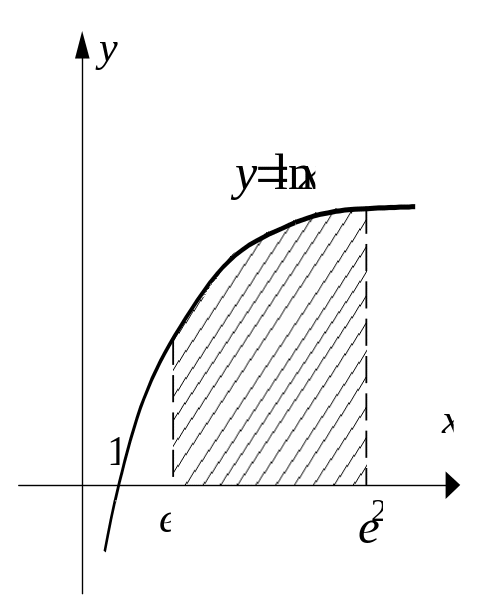
Рис. 12
Решение. Воспользуемся формулой (1):


![]()
![]()
![]()
![]()
![]() (кв.
ед.).
(кв.
ед.).
Задача
2. Найти
площадь фигуры, ограниченной графиком
функции
![]() (рис. 13).
(рис. 13).
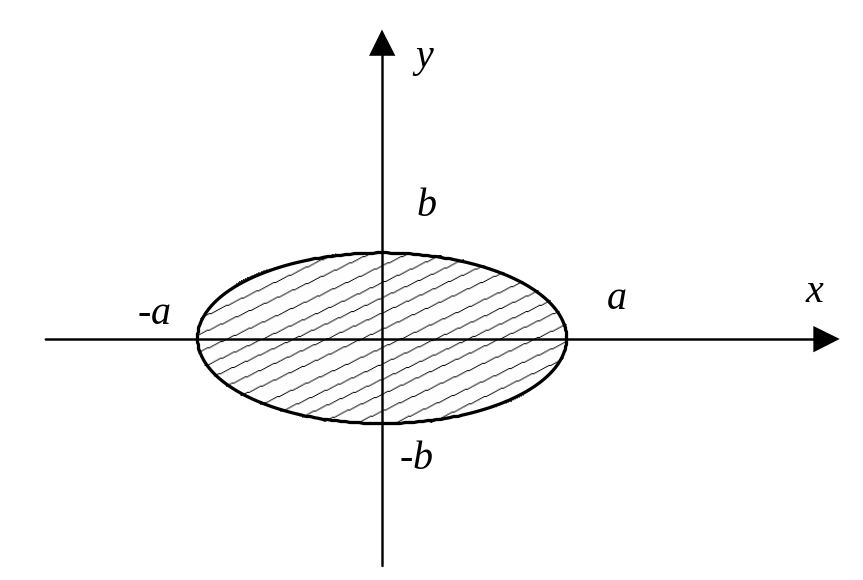
Рис. 13
Решение.
Так как кривая является уравнением
эллипса, симметричным относительно
осей координат, то площадь данной фигуры
можно вычислить в первой четверти по
формуле (1), а результат умножить на 4. Из
уравнения эллипса выразим у
через х,
т.е.
![]() .
Тогда:
.
Тогда:
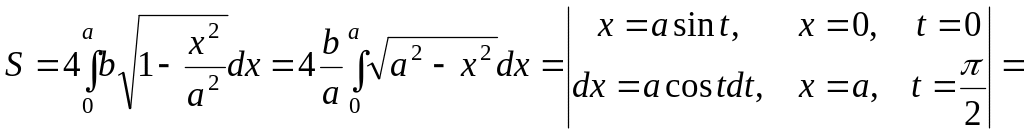


![]() (кв.
ед.).
(кв.
ед.).
Задача
3. Найти
площадь фигуры, ограниченной графиками
функций
![]() и осью Оу
(рис. 14).
и осью Оу
(рис. 14).
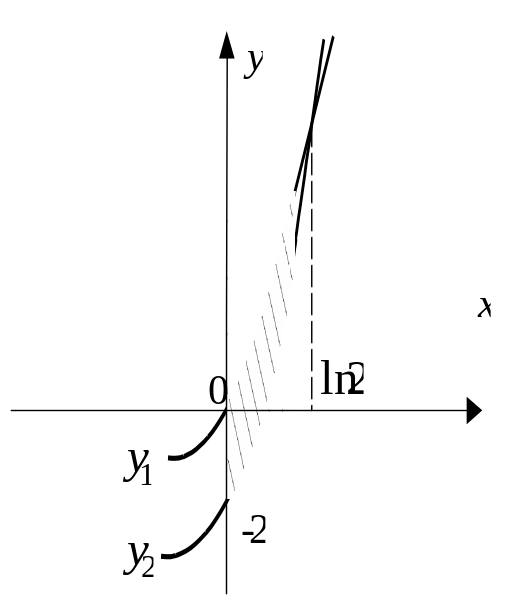
Рис. 14
Решение. Для нахождения площади необходимо определить пределы интегрирования. Для этого найдем точку пересечения графиков функций, приравняв правые части уравнений .
![]()
![]()
![]() .
.
Тогда по формуле (4)
![]()
![]()
(кв. ед.).
Решить задачу по образцу:
Задача
4. Вычислить
площадь фигуры, ограниченной линиями:
![]() .
.
Задача
5. Найти
площадь петли, ограниченной графиком
функции, заданной параметрически
![]() (рис. 15).
(рис. 15).
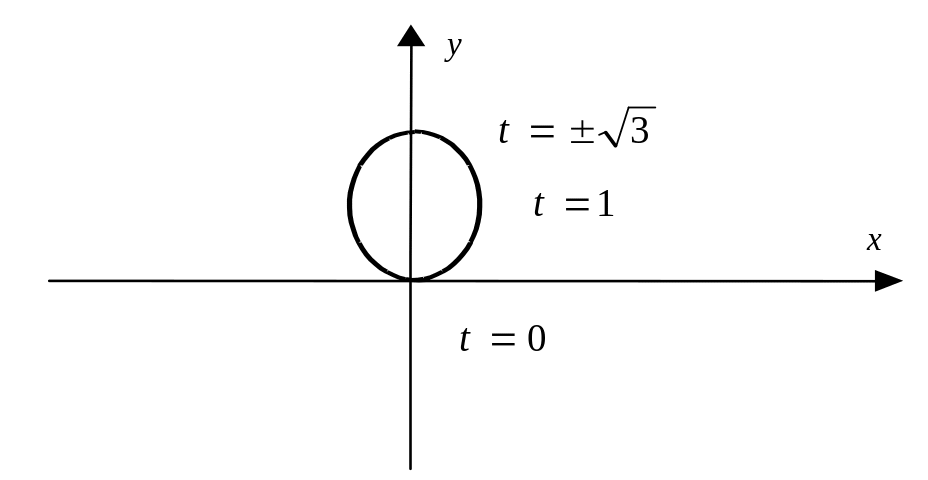
Рис. 15
Решение.
Воспользуемся симметрией фигуры и
найдем половину искомой площади, умножив
на 2. Так как петля вытянута вдоль оси
Оу,
то воспользуемся формулой
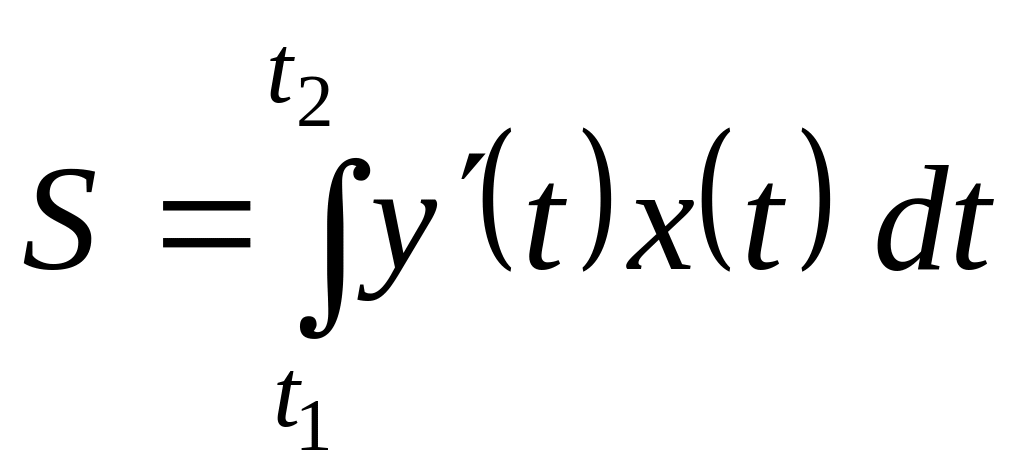 (см. формулу (5)),
(см. формулу (5)),
![]() .
.
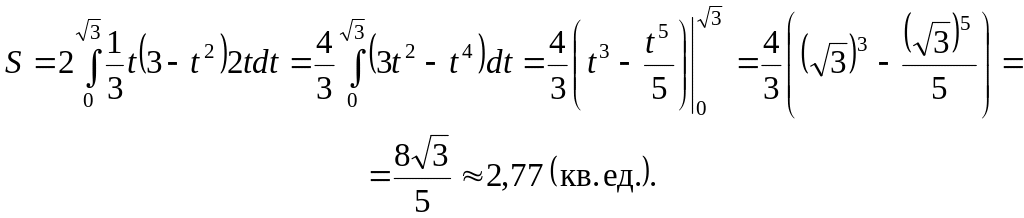
Решить задачу по образцу:
Задача
6. Найти
площадь фигуры, заданной уравнением
![]()
Задача
7. Найти
площадь одного лепестка, где
![]() (рис. 16).
(рис. 16).

Рис. 16
Решение. Найдем площадь по формуле (6):

![]() (кв.ед.).
(кв.ед.).
Решить задачу по образцу:
Задача 8. Найти площадь, ограниченную кардиоидой:
![]() .
.
