
- •Тема 1. Введение в анализ
- •Краткие сведения из теории
- •Задание для студентов
- •Основные теоремы о пределах
- •1. Раскрытие неопределенности вида
- •2. Раскрытие неопределенности вида
- •3. Вычисление значений сложной функции
- •Тема 2. Дифференциальное исчисление функции одной переменной
- •Краткая информация о новых учебных элементах
- •Основные формулы дифференцирования
- •Занятие №1. Задачи, приводящие к понятию производной
- •Итак, исходя из условия задачи, найдем координаты точки касания м : , получим
- •Задание для самостоятельной работы
- •Занятие №2. Производная сложной функции
- •Ход занятия
- •Задание для самостоятельной работы
- •Разобрать решение задач:
- •Занятие №3. Производная сложной функции (продолжение)
- •Ход занятия
- •Вычисление производной функции в данной точке
- •Задание для самостоятельной работы
- •Занятие №4. Дифференцирование функций
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы Задача 11. Найти от следующих функций:
- •Занятие №5. Дифференциал функции
- •Краткая информация о новых учебных элементах
- •Основные свойства дифференциала
- •Задание для самостоятельной работы
- •Занятие №6. Подготовка к контрольной работе по теме 2
- •Решить самостоятельно:
- •Задание для самостоятельной работы
- •Занятие №7. Вычисление пределов с помощью производной
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Для решения кубического уравнения
- •Задание для самостоятельной работы
- •Тема 3. Комплексные числа
- •Краткая информация о новых учебных элементах
- •1. Комплексные числа и их геометрическая интерпретация
- •2. Действия над комплексными числами, заданными алгебраической формой
- •3. Перевод комплексных чисел из алгебраической формы записи в тригонометрическую и показательную и обратно
- •4. Действия над комплексными числами в тригонометрической форме
- •5. Действия над комплексными числами в показательной форме записи
- •Занятие №1. Комплексные числа
- •Задание для самостоятельной работы
- •Занятие №2. Комплексные числа (продолжение)
- •Задание для самостоятельной работы
- •Тема 4. Неопределенный интеграл Введение
- •Свойства неопределенного интеграла
- •Занятие №1. Непосредственное интегрирование функций
- •Ход занятия Краткая информация о новых учебных элементах
- •Геометрическая иллюстрация неопределенного интеграла
- •Задание для самостоятельной работы
- •Занятие №2. Метод замены переменных
- •Краткая информация о новых учебных элементах
- •Задание для студентов
- •Задание для самостоятельной работы
- •Занятие №3. Метод интегрирования по частям
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Занятие №4. Метод интегрирования по частям (продолжение)
- •Учебные вопросы
- •Задание для самостоятельной работы
- •Занятие №5. Интегрирование рациональных дробей
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Занятие №6. Интегрирование рациональных дробей (продолжение)
- •Алгоритм нахождения интеграла методом неопределенных коэффициентов
- •Задача 6. Найти интегралы методом неопределенных коэффициентов:
- •Задание для самостоятельной работы
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Занятие №9. Интегрирование некоторых иррациональных функций
- •Краткая информация о новых учебных элементах
- •Занятие №11. Контрольная работа по теме «Неопределенный интеграл»
- •Образец одного из вариантов
- •Занятие №12. Анализ контрольной работы
- •Задание для самостоятельной работы
- •Тема 5. Определенный интеграл
- •Краткие сведения из теории
- •Основные свойства определенного интеграла
- •1. Несобственные интегралы первого рода
- •2. Несобственные интегралы второго рода
- •Задача 3. Исследовать на сходимость интеграл .
- •1. Площадь плоской фигуры
- •2. Длина дуги плоской кривой
- •3. Площадь поверхности фигуры вращения
- •4. Объем тела
- •Задание для самостоятельной работы
- •Занятие №5. Геометрическое приложение определенного интеграла (продолжение)
- •Задача 11. Найти площадь поверхности фигуры при вращении её вокруг полярной оси.
- •Задание для самостоятельной работы
- •Занятие №6. Механическое приложение определенного интеграла
- •Краткая информация о новых учебных элементах
- •Задача 5. Определить величину давления морской воды на вертикальный круг радиуса м, центр которого погружен в воду на глубину м. Плотность морской воды кг/ .
- •Задача 10. Найти координаты масс однородной дуги окружности радиусом r с центральным углом . Задание для самостоятельной работы
1. Несобственные интегралы первого рода
Несобственные интегралы с бесконечными пределами (или I рода) (рис. 2) определяются следующим образом:
 (1)
(1)

Рис. 2
Несобственные интегралы I рода называются сходящимися, если существуют конечные пределы, стоящие в правых частях равенств (1). Если же указанные пределы не существуют или бесконечны, то несобственные интегралы называются расходящимися.
Для установления сходимости интегралов (1) можно воспользоваться следующими признаками:
Если на промежутке
 непрерывные функции
и
непрерывные функции
и
 удовлетворяют условию
удовлетворяют условию
 ,
то из сходимости интеграла
,
то из сходимости интеграла
 следует сходимость интеграла
следует сходимость интеграла
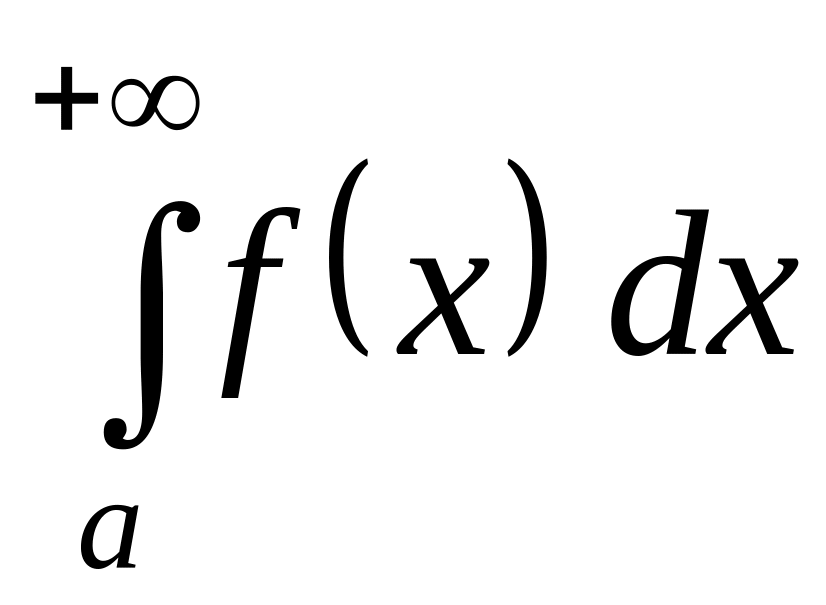 ,
а из расходимости интеграла
следует расходимость интеграла
,
а из расходимости интеграла
следует расходимость интеграла
 («признак сравнения»).
(«признак сравнения»).Если при
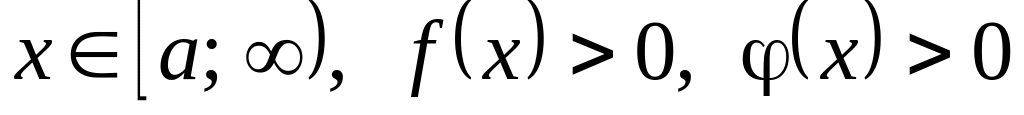 и существует конечный предел
и существует конечный предел
 ,
то интегралы
и
сходятся или расходятся одновременно
(«предельный признак сравнения»).
,
то интегралы
и
сходятся или расходятся одновременно
(«предельный признак сравнения»).Если сходится интеграл
 ,
то сходится и интеграл
,
который в этом случае называется
абсолютно
сходящимся.
,
то сходится и интеграл
,
который в этом случае называется
абсолютно
сходящимся.
2. Несобственные интегралы второго рода
Если
функция
непрерывна в промежутке
![]() и имеет разрыв
II-го
рода при
и имеет разрыв
II-го
рода при
![]() ,
то несобственный интеграл от неограниченной
функции (II
рода) определяется следующим образом:
,
то несобственный интеграл от неограниченной
функции (II
рода) определяется следующим образом:
![]() . (2)
. (2)
Аналогично, если функция терпит бесконечный разрыв в точке , то полагают
![]() . (3)
. (3)
Если
функция
терпит разрыв
II-го
рода во внутренней точке
![]() (рис. 3), то несобственный интеграл второго
рода определяется формулой
(рис. 3), то несобственный интеграл второго
рода определяется формулой
 . (4)
. (4)
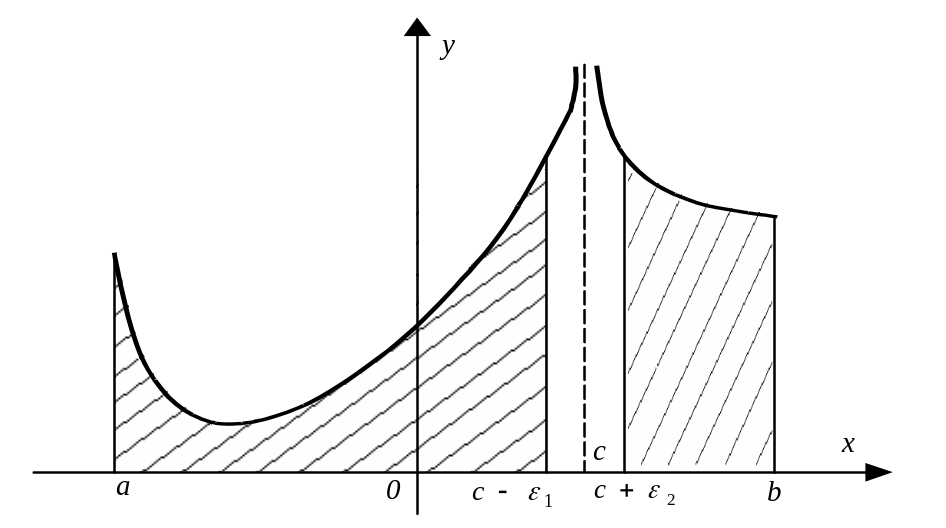
Рис .3
Если пределы, стоящие в правой части равенств (2), (3), (4) существуют, то несобственные интегралы II рода называются сходящимися; в противном случае – расходящимися.
Для установления сходимости интегралов (2)-(4) можно воспользоваться следующими признаками:
Если на промежутке непрерывные функции и при терпят разрыв II-го рода и удовлетворяют условию , то из сходимости интеграла
 следует сходимость интеграла
следует сходимость интеграла
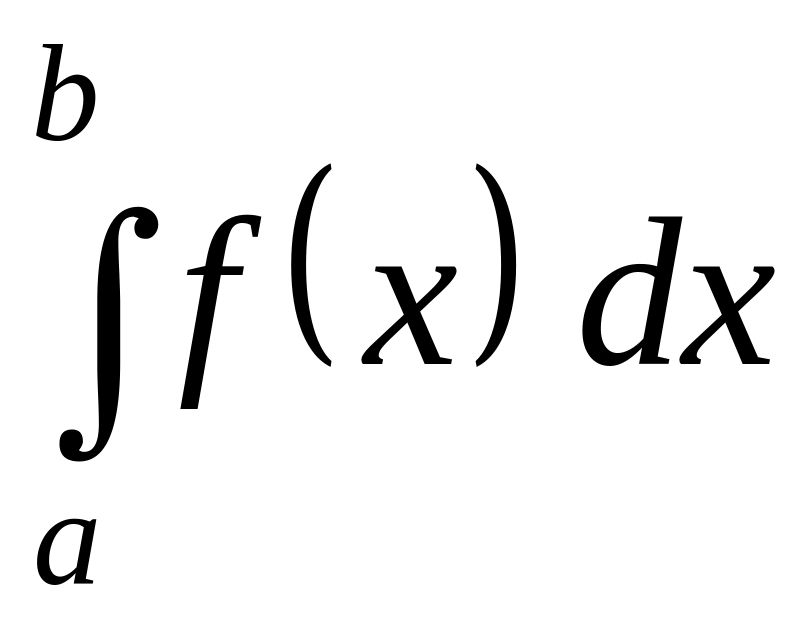 ,
а из расходимости интеграла
следует расходимость интеграла
(«признак сравнения»).
,
а из расходимости интеграла
следует расходимость интеграла
(«признак сравнения»).Пусть функции и непрерывны на промежутке и в точке терпят разрыв II рода. Если существует конечный предел
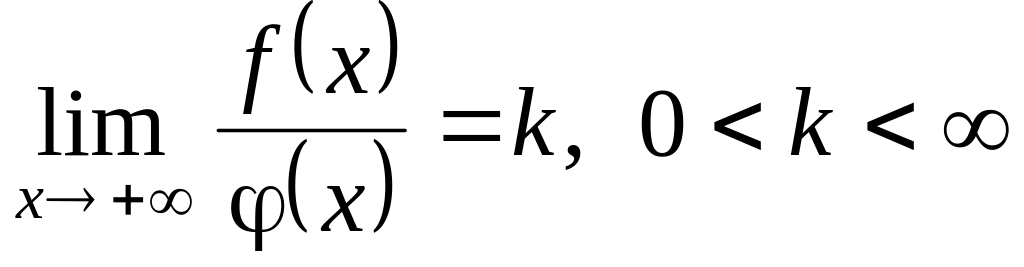 ,
то интегралы
и
сходятся или расходятся одновременно
(«предельный признак сравнения»).
,
то интегралы
и
сходятся или расходятся одновременно
(«предельный признак сравнения»).Если функция , знакопеременная на отрезке , имеет разрыв в точке и несобственный интеграл
 сходится, то сходится и интеграл
,
который в этом случае называется
абсолютно
сходящимся.
сходится, то сходится и интеграл
,
который в этом случае называется
абсолютно
сходящимся.
Задача
1. Дан интеграл
![]() .
Установить, при каких значениях
.
Установить, при каких значениях
![]() этот интеграл сходится, а при каких –
расходится.
этот интеграл сходится, а при каких –
расходится.
Решение.
Предположим, что
![]() .
Тогда
.
Тогда
![]()
Следовательно,
если
![]() ,
то
,
то
![]() ,
,
т.е. данный интеграл сходится.
Если
![]() ,
то
,
то
![]() ,
,
т.е. данный интеграл расходится.
Если
![]() ,
то
,
то
![]() ,
,
т.е. данный интеграл расходится.
Задача
2. Исследовать
сходимость несобственного интеграла
![]() .
.
Решение. По определению несобственного интеграла I рода
![]()
![]() ,
,
интеграл
расходится, т.к.
![]() и
и
![]() не существуют.
не существуют.
Задача 3. Исследовать на сходимость интеграл .
Решение.
Здесь
![]() при
при![]() ,
при этом
,
при этом
 .
Но интеграл
.
Но интеграл
![]() расходится, так как
расходится, так как
 .
.
Поэтому, согласно признаку сравнения, интеграл расходится.
Задача
4. Вычислить
несобственный интеграл
![]()
Решение.
Подынтегральная функция
![]() определена и непрерывна на всей числовой
оси. Эта функция является четной.
Следовательно,
определена и непрерывна на всей числовой
оси. Эта функция является четной.
Следовательно,
![]() .
.
Тогда имеем:
![]() .
.
Интеграл
сходится. Следовательно, исходный
интеграл также сходится и равен
![]() .
.
Задача 5. Найти значение несобственных интегралов или установить их расходимость (решить задачи по образцу):
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Задача
6. Вычислить
несобственный интеграл
![]() .
.
Решение. Подынтегральная функция терпит бесконечный разрыв в точке . Следовательно,
![]()
![]() ,
,
т.е. данный интеграл сходится.
Задача 7. Исследовать несобственный интеграл на сходимость
![]() .
.
Решение.
Подынтегральная функция терпит разрыв
в точке
.
Очевидно, что при
![]()
![]() .
.
Так как несобственный интеграл
![]() ,
,
т.е. сходится, то сходится и исходный интеграл.
Задача 8. Исследовать несобственные интегралы на сходимость (по образцу задач 6,7):
 ;
;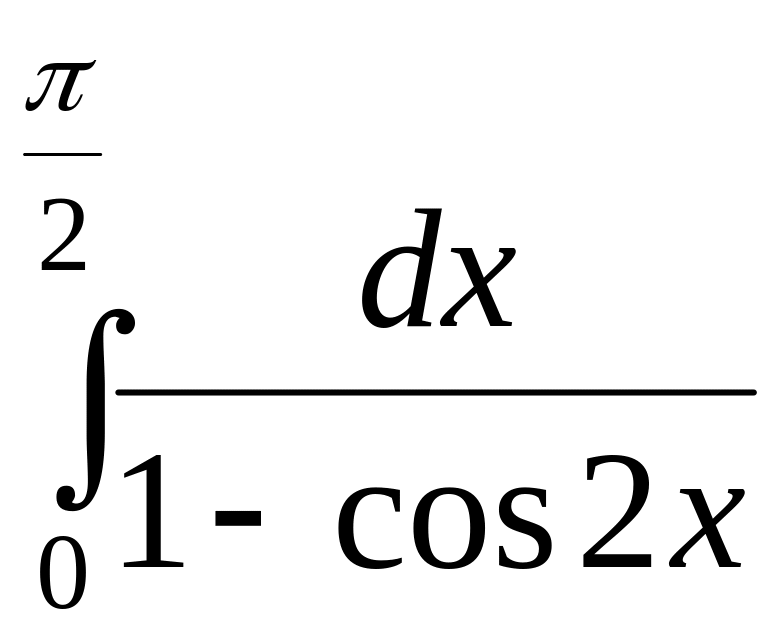 ;
; .
.
Задание для самостоятельной работы
Исследовать несобственные интегралы на сходимость:
Задача 9.
![]() .
.
Задача 10.
![]() .
.
Задача
11.
![]() .
.
Задача
12.
![]() .
.
Задача
13.
 .
.
Задача
14.
![]() .
.
Занятие №4. Геометрическое приложение определенного интеграла
Цель занятия: закрепить правила вычисления определенных интегралов на уровне знания и умения решать типовые задачи по теме; уметь применять определенные интегралы к решению прикладных задач геометрии.
Краткая информация о новых учебных элементах
Определенный интеграл в случае, когда , , с геометрической точки зрения определяет площадь криволинейной трапеции. Площадь всякой плоской фигуры можно рассматривать как сумму или разность площадей некоторых криволинейных трапеций. Это означает, что с помощью определенных интегралов можно вычислять площади различных плоских фигур.
