Введение

Предлагаемое пособие охватывает начальный курс математического анализа.

В пособии излагаются определения основных учебных элементов, свойства пределов, производной, интеграла (определенного и неопределенного) функции одной переменной, а также их геометрический и физический смысл. Предполагается, что более глубокое изучение рассматриваемых тем студенты проводят по лекциям и по учебным пособиям самостоятельно.

В пособии разобраны решения большого количества примеров, что позволит студентам самостоятельно провести анализ и выполнение остальных задач.

Данное пособие предназначено для студентов технических специальностей и преподавателей, ведущих практические занятия у студентов технических специальностей.

Тема 1. Введение в анализ

Занятие №1. Пределы

Цель занятия: усвоить учебные элементы на уровне знаний. Закрепить навыки вычисления значения функции в точке, а также навыки вычисления пределов. Учитывая, что учебные элементы этого занятия знакомы студентам из средней школы, уделить особое внимание структуре сложной функции.

Краткие сведения из теории

Определение 1. Функция у от х, заданная цепью равенств , где , называется сложной или функцией от функции.

Определение 2. Говорят, что , если для любого такое, что при .

Определение 3. Если , то функция называется бесконечно малой при . Заметим, что если - бесконечно малая, то - бесконечно большая величина.

ТЕОРЕМА 1. (первый замечательный предел):

.

Основные эквивалентности при

1. где п и 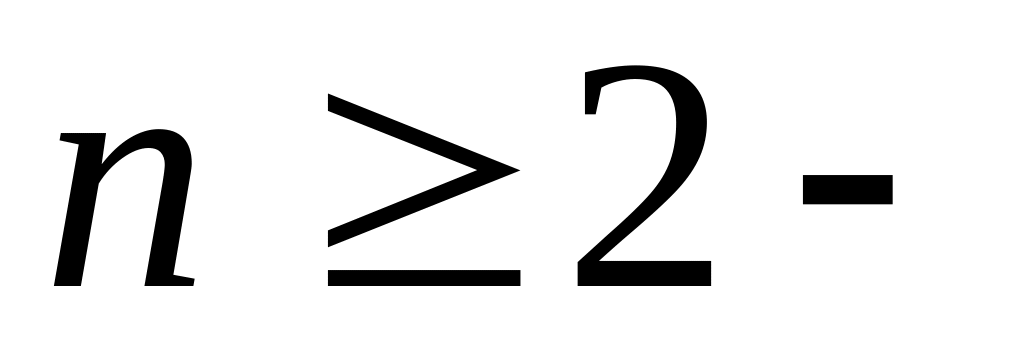натуральные;

2. ;

3. ;

4. ;

5. , где ;

6. 

7. 

8. 

9. 

10. 

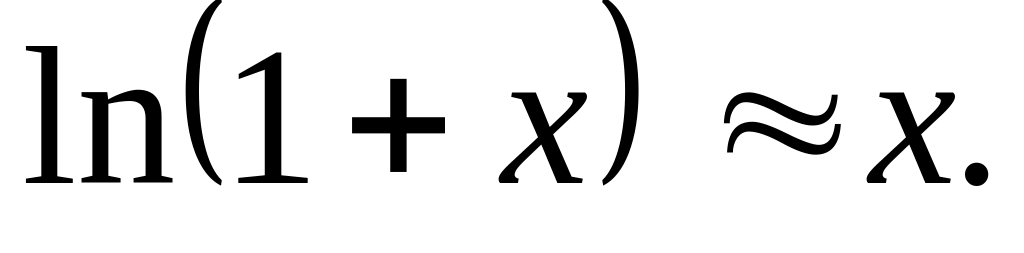
Задание для студентов

Исходя из этих формул, приближенно вычислить:

.

Сравнить полученные значения с табличными данными.

Задание. Даны функции:

.

Вычислить:

;

.

Основные теоремы о пределах

ТЕОРЕМА 2. Если предел функции существует при , то он единственный.

ТЕОРЕМА 3. .

ТЕОРЕМА 4. .

Следствие 1. .

Следствие 2. .

ТЕОРЕМА 5. .

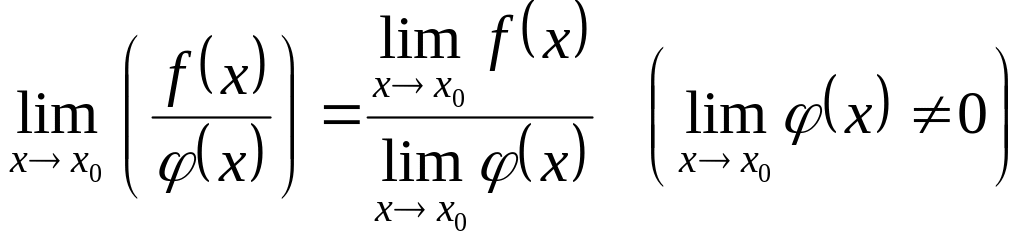1. Раскрытие неопределенности вида

Для решения задач данного типа надо числитель и знаменатель дроби разделить на степень с наибольшим показателем в знаменателе.

Задача 1. .

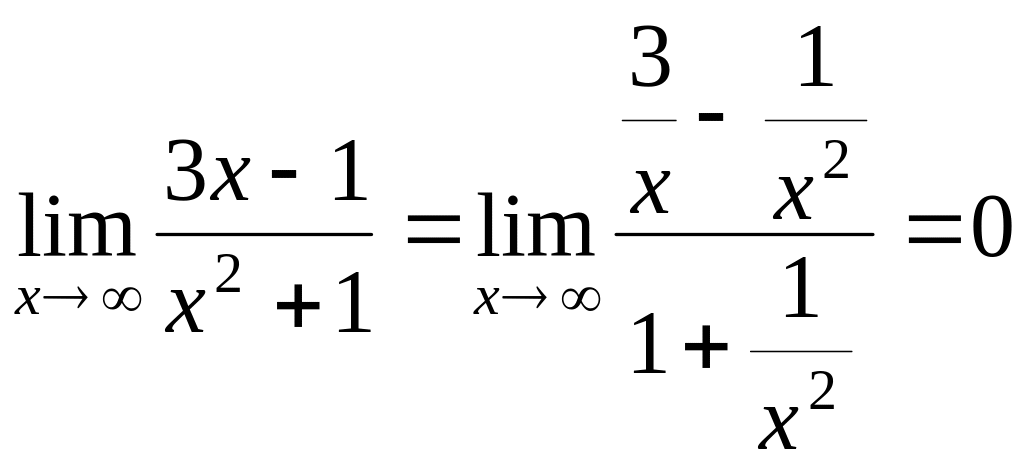Делим числитель и знаменатель на степень . Величины и являются бесконечно малыми при , поэтому и .

Применяя теорему о пределе частного (она применима, так как предел знаменателя равен 1, т.е. отличен от 0), получаем окончательный ответ.

Задача 2. Вычислить:

.

Задача 3. Вычислить:

.

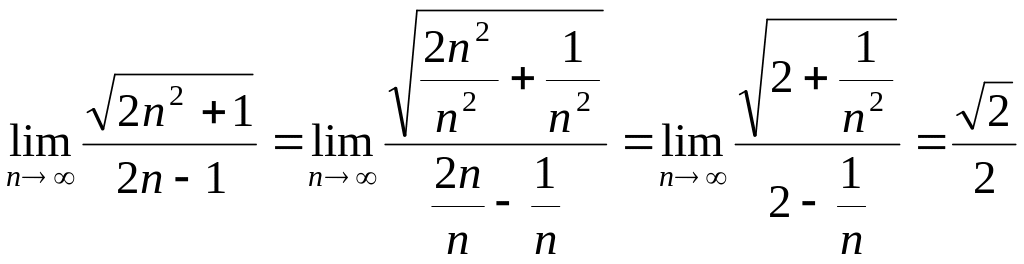Решить самостоятельно (вычислить пределы):

Задача 4. .

Задача 5. .

Задача 6. .

Задача 7. .

Задача 8. .

2. Раскрытие неопределенности вида

Задача 9. .

Вычислим корни трехчлена : и разложим его на множители по формуле:

;

.

Сократим дробь и вычислим предел, подставляя вместо х число 2.

Задача 10. Решается аналогично. Вычислить: .

Задача 11. Вычислить .

Заменим , тогда и

.

Задача 12. .

Задача 13. .

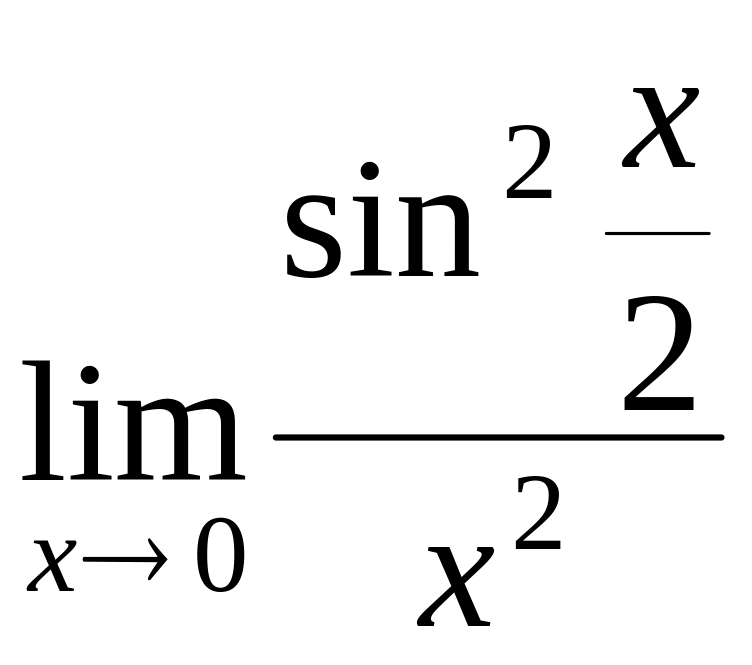Задача 14. .

Задача 15. .

3. Вычисление значений сложной функции

Задача 16. ; .

Найти значения этой функции в точках .

х	0
u	16	15	12	0
	4			0

Задача 17. . Ввести промежуточный аргумент, найти значения этой функции при ; .

х	0
и	16
	1

Задача 18. . Ввести промежуточный аргумент, вычислить .

Задача 19. а) . Ввести промежуточный аргумент и и заполнить таблицу:

х	0
и
у

б) - условие то же, .

Задача 20. Составить сложную функцию и найти ее значение в трех заданных точках.

Задание для самостоятельной работы

Найти пределы:

Задача 21. .

Задача 22. .

Задача 23. .

Задача 24. .

Задача 25. .

Задача 26. .

Задача 27. .

Задача 28. .

Задача 29. .

Занятие №2. Второй замечательный предел

Краткая информация о новых учебных элементах

ТЕОРЕМА (второй замечательный предел):

где ,

или .

Задача 1. Вычислить .

Решение. Заменим , тогда и

.

Задача 2. Вычислить .

Решение. Заменим , тогда и

.

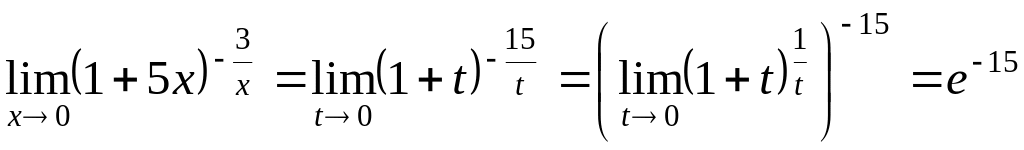Задание для самостоятельной работы

Вычислить пределы:

Задача 3. .

Задача 4. .

Задача 5. .

Задача 6. .

Задача 7. .

Занятие №3. Непрерывность функции

Краткая информация о новых учебных элементах

Пусть функция определена в некоторой точке и в некоторой ее окрестности.

Определение 1. Функция называется непрерывной в точке , если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.

.

При нахождении предела непрерывной функции можно перейти к пределу под знаком функции.

Задача 1. .

Функция называется непрерывной в интервале , если она непрерывна в каждой точке этого интервала.

Определение 2. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Точка разрыва называется точкой разрыва первого рода функции , если в этой точке существуют конечные пределы функции слева и справа, но не равные между собой; если эти конечные односторонние пределы равны, то точка разрыва первого рода называется точкой устранимого разрыва.

Точка разрыва называется точкой разрыва второго рода функции , если хотя бы один из односторонних пределов не существует или равен бесконечности.

Задача 2. Исследовать на непрерывность и построить график функции

Решение. Функции и непрерывны на всей числовой прямой, поэтому данная функция может иметь разрывы только в точках, где меняется ее аналитическое выражение, т.е. в точках и

Исследуем функцию на непрерывность в этих точках, для чего найдем соответствующие односторонние пределы и значения функции.

Рис. 1

В точке имеем: , но значение функции не определено. Отсюда следует, что точка устранимого разрыва для функции . В точке имеем: Таким образом, в этой точке , т.е. функция имеет разрыв 1-го рода и непрерывна слева.

Скачок функции в точке равен

Построим график этой функции (рис. 1).

Установить характер точек разрыва:

Задача 3. .

Задача 4. .

Задача 5. .

Задача 6.

Задача 7. Используя свойства непрерывных функций, доказать, что функция непрерывна на промежутке .

а)

б)