Лабораторна робота № 9

Тема. Побудова моделі при наявності автокореляції залишків

Мета заняття: засвоїти методи перевірки автокореляції залишків; навчитись будувати економетричну модель з урахуванням автокореляції.

Постановка задачі:

• На основі вихідних даних побудувати модель даної залежності у вигляді лінійного рівняння.

• Знайти оцінки параметрів лінії регресії по даній стохастичній залежності.

• Оцінити адекватність моделі статистичним даним з імовірністю Р=0,95.

• З імовірністю Р=0,95 визначити наявність автокореляції в залишках.

• У випадку наявності автокореляції в залишках, побудувати модель даної залежності за допомогою методу Ейткена.

• Визначити наявність автокореляції у залишках для отриманої моделі. Зробити висновки.

• З імовірністю Р=0,95 визначити адекватність отриманої моделі експериментальним даним.

Короткі теоретичні відомості

В економетричних дослідженнях часто зустрічаються такі випадки, коли дисперсія залишків є постійною, але спостерігається їх коваріація. Це явище має назву автокореляції залишків.

Автокореляція залишків виникає частіше за все тоді, коли економетрична модель будується на основі часових рядів. При автокореляції залишків, як і при гетероскедастичності, дисперсія залишків запишеться:

,

Але тут – матриця матриця коваріацій залишків, матиме зовсім інший вигляд, а саме:

.

У даній матриці параметр  характеризує коваріацію кожного наступного значення залишків із попереднім. Так, якщо залишки задовольняють авторегресійній моделі першого порядку:

,

то  характеризує силу зв’язку величини залишків у період t від величини залишків у період t – 1 (у попередній період).

Якщо проігнорувати явище автокореляції у вихідних даних, оцінки параметрів моделі, отримані методом 1МНК будуть неефективними, що приводить і до неефективності прогнозів, побудованих за допомогою такої моделі. Для перевірки наявності автокореляції застосовуються критерії:

1. Критерій Дарбіна—Уотсона;

2. Критерій фон Неймана;

3. Нециклічний коефіцієнт автокореляції;

4. Циклічний коефіцієнт автокореляції.

За наявності автокореляції, для побудови моделі краще використовувати узагальнений метод найменших квадратів Ейткена

або

,

де – матриця, обернена до матриці ;

– матриця, обернена до матриці .

На практиці для розрахунку параметра  використовується співвідношення:

,

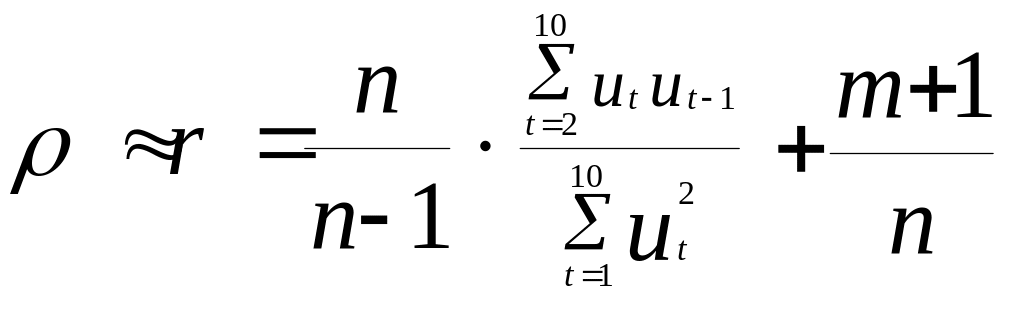де кількість спостережень, кількість змінних моделі;

тобто він дорівнює циклічному коефіцієнта автокореляції з поправкою на величину зміщення.

Хід роботи

1. Завантажити програму EXCEL.

2. Сформувати таблицю вихідних даних, заповнивши діапазон комірок А3:С12 (див. рис 9.1).

3. Знайти об’єм вибірки n за допомогою вбудованої функції ЧСТРОК.

4. Для побудові рівняння лінійної регресії для вихідних даних, скористаємося функціями НАКЛОН – яка повертає значення кутового коефіцієнта рівняння лінійної регресії, і ОТРЕЗОК, яка повертає ординату точки перетину лінії регресії з віссю OY.

5. Для подальшого використання нам необхідні значення та що знаходяться у комірках K3 і K4. Щоб уникнути абсолютних посилань на ці комірки, скористаємося ще однією можливістю EXCEL – створення імен. На такі імена можна в подальшому посилатися, як на вбудовані константи або змінні. Для цього:

– ставимо курсор у комірку K3, де знаходиться значення ;

– у підрозділі ВСТАВКА головного меню вибираємо пункт Имя і далі підпункт Присвоить;

– у відкритому вікні цієї команди у полі Формула вказуємо адресу комірки, у якій знаходиться дана величина, а у полі Имя задаємо її ім’я .

Так можна створити імена: n – кількість спостережень; Ra0 – константа ; Ra1 – константа .

6. Знайти:

– розрахункові значення показника ;

– залишки моделі та їх квадрати відповідно ;

– різниці відповідного і попереднього залишку моделі ;

– квадрати отриманих різниць ;

– добутки відповідного і попереднього залишків моделі ;

– суми по відповідним стовпчикам.

7. Знайти необхідні статистики:

дисперсію показника ,

дисперсию залишків ,

коефіцієнт детермінації ,

коефіцієнт кореляції .

8. Розрахувати критерій Дарбіна-Уотсона за формулою:

.

9. Порівняємо розрахункове значення критерію DW з табличним. Зокрема, для випадку, представленому на рис 9.1, DW_крит знаходимо для =0,05, n=10 і m=1. Критичні значення критерію DW у цьому випадку: DW₁=0,879 – нижня межа; DW₂=1,320 – верхня межа. Оскільки DWфакт < DW₁ , то при можна стверджувати, що залишки u_t мають додатню автокореляцію.

Наявність чи відсутність автокореляції залишків можна також визначити на основі критерію фон Неймана.

10. Розрахувати критерій фон Неймана за формулою:

.

11. Фактичне значення критерію фон Неймана порівнюється з табличним при вибраному рівні довіри  і заданому числі спостережень n. Якщо Q_факт < Q_табл , то існує додатня автокореляція залишків. Так, для випадка, представленого на рис.9.1, знайдено Q_табл для =0,05 і n=10.

У випадку, зображеному на рис. 9.1, отримані значення критеріїв дають підставу до прийняття гіпотези про наявність автокореляції.

Для побудови нової моделі скористаємося методом Ейткена. Оператор оцінювання цим методом записується так:

,

де — матриця, обернена до матриці .

Матриця — матриця коваріацій залишків, у даному випадку при десяти спостереженнях, має вигляд:

;

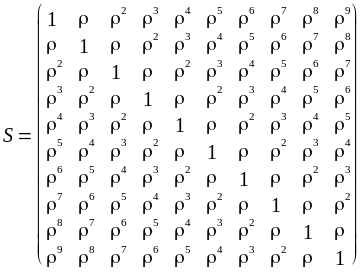12. Обчислити параметр .

13. Побудувати матрицю .

14. Побудувати обернену до матрицю. Хоча в EXEL є функція для знаходження оберненої матриці, але вона дає наближений результат, тому в даному випадку побудуємо обернену матрицю самостійно, скориставшись формулою:

.

Відповідний діапазон у режимі відображення формул показано на рис. 9.2. Той самий діапазон показано на рис. 9.3 у режимі відображення значень.

15. Знайти матриці , та . Тут можна скористатися вбудованими функціями МУМНОЖ, МОБР.

16. Знайти матрицю .

17. Розрахувати всі необхідні для подальшого дані, а саме:

– нові розрахункові значення показника з оцінками параметрів та ;

– залишки моделі ;

– квадрати залишків моделі ;

– різниці відповідного і попереднього залишків моделі ;

– квадрати різниці відповідного і попереднього залишків моделі ;

– суми по відповідних рядках.

18. Розрахувати нове значення критерію Дарбіна-Уотсона

.

Порівняти його з критичним значенням при n=10 і =0,05, зробити висновок про наявність автокореляції в новій моделі. У випадку, зображеному на рис. 9.2, 9.3, коли DW_факт< DW₁, дійдемо висновку, що ми не звільнились від автокореляції залишків. Це означає, що вихідна гіпотеза, коли залишки описуються авторегресійною схемою першого порядку, не дотримується.

Якщо залишки описуються авторегресійною схемою більш високого порядку, то доцільно виконати оцінку параметрів моделі методом Кочрена-Оркатта або Дарбіна.

19. Н а рис. 9.1, 9.2 та 9.3 показано, як може виглядати робочий лист EXCEL після виконання роботи.