Короткі теоретичні відомості

Виробнича функція Кобба-Дугласа має вигляд степеневої функції двох змінних:

,

де показник – це обсяг виробництва, фактори – чисельність робочої сили та – обсяг основних фондів. За допомогою операції логарифмування ця залежність перетворюється на лінійну:

,

де , , , ,

параметри якої знаходяться за допомогою методу найменших квадратів.

Частинні коефіцієнти еластичності моделі , . Вони є показниками росту функції відносно відповідних змінних. Сумарний коефіцієнт еластичності цієї моделі дорівнює сумі . Це означає що зміна факторів у разів призведе до зміни показника у разів.

Ізоквантою називається множина точок з координатами ( ), де та – значення факторів, для яких показник обсягу виробництва продукції залишається сталим.

Хід роботи

1. Завантажити програму EXCEL.

2. Сформувати масив вихідних даних (див. рис.6.1, діап. A2:D14).

3. Висувається гіпотеза, що модель обсягу випуску продукції має вигляд:

де – обсяг випущеної продукції, – працезатрати; – основні засоби розглянутої галузі.

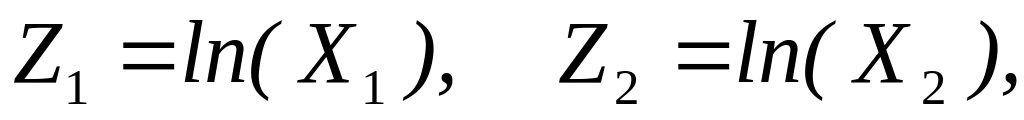
4. Для приведення залежності до лінійного вигляду зробимо заміну змінних: 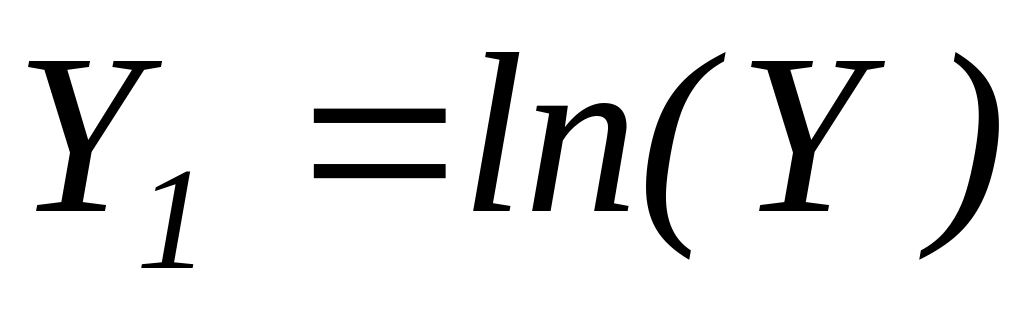. Відповідні розрахунки занесемо до таблиці.

5. Знаходимо оцінки параметрів лінійної моделі:

,

за алгоритмом, вказаним у роботі № 4 (див. рис. 6.1).

6. Тоді модель за вихідними даними буде мати вигляд:

,

де .

7. Для аналізу моделі зробити наступні розрахунки:

– знайти розрахункове значення показника або ;

– знайти різниці розрахункових і відповідних фактичних значень показника;

– знайти квадрати цих різниць і суми квадратів.

Відповідні розрахунки занести до таблиці (див. рис. 6.1).

8. Знайти дисперсію показника, дисперсію помилок моделі, коефіцієнти детермінації та кореляції (відповідні формули знайти в роб. № 4 та 5). Зробити відповідні висновки.

9. Знайти розрахункове значення критерію Фішера (формули див роб. № 4 та роб. № 5). Знайти критичне значення критерію Фішера відповідно до прийнятого рівня значущості та числа ступенів свободи 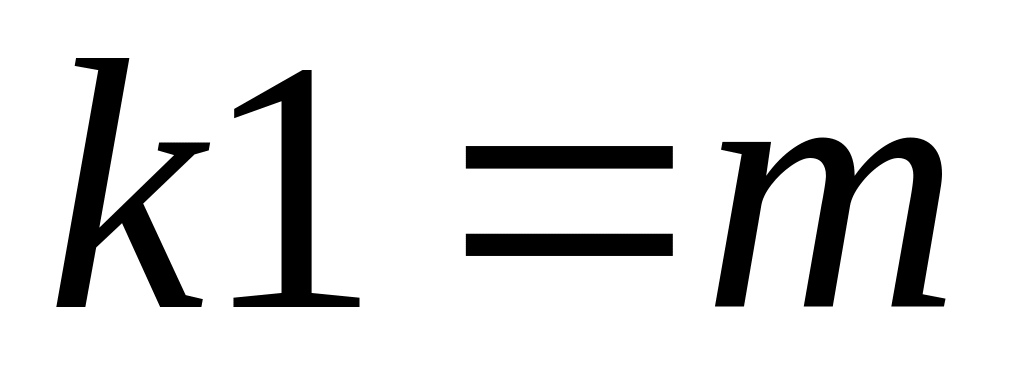, 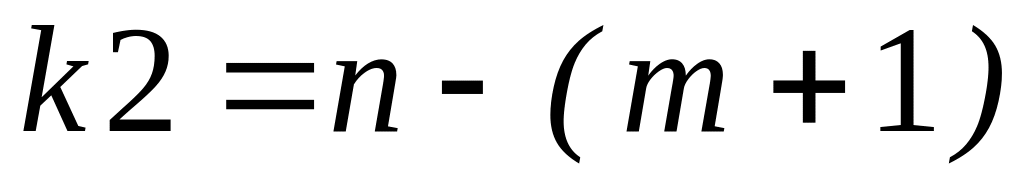. Порівняти табличне значення з розрахунковим та зробити висновки.

10. Якщо модель адекватна, виконуємо прогноз за цією моделлю. Задаємо значення факторів та та знаходимо відповідні 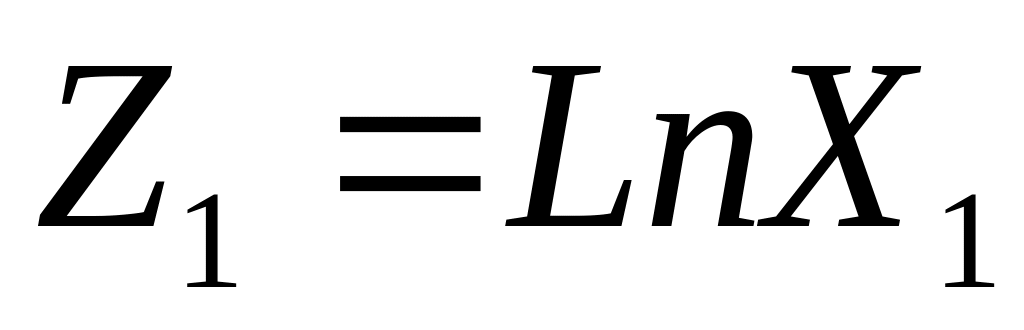та (див. рис. 6.2).

11. Для лінійної моделі з прогнозними значеннями 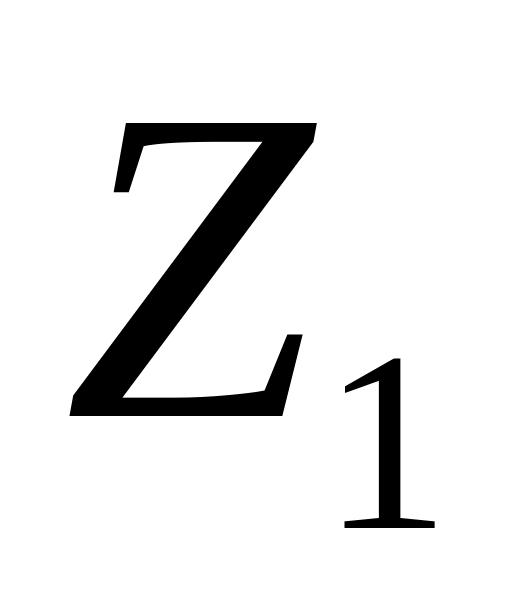та 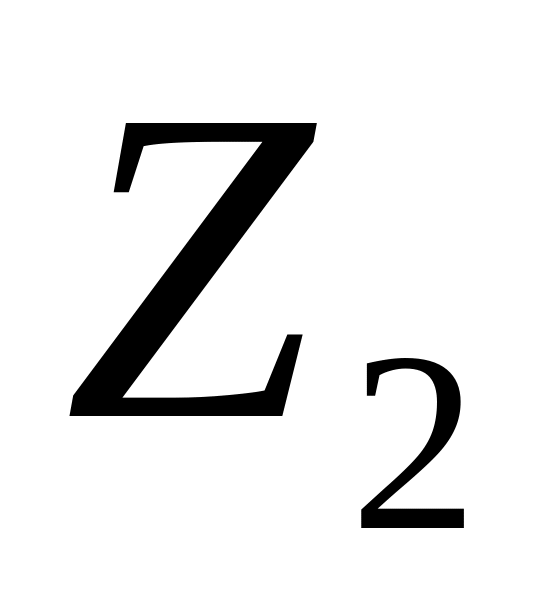будуємо прогноз (формули див. роб. № 4).

12. Тоді прогноз для дійсного значення показника буде в межах: 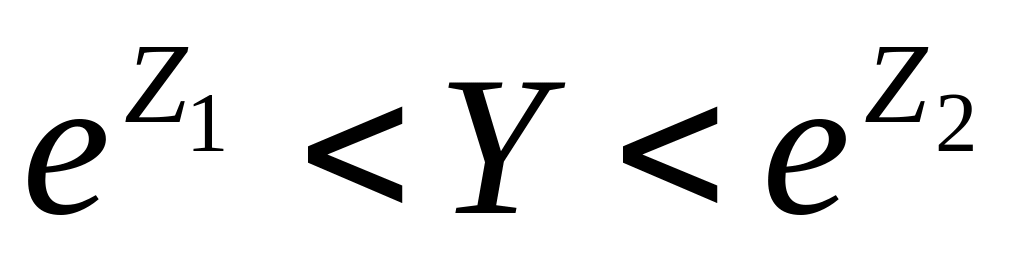(див. рис. 6.2).

13. Розрахуємо сумарний коефіцієнт еластичності .

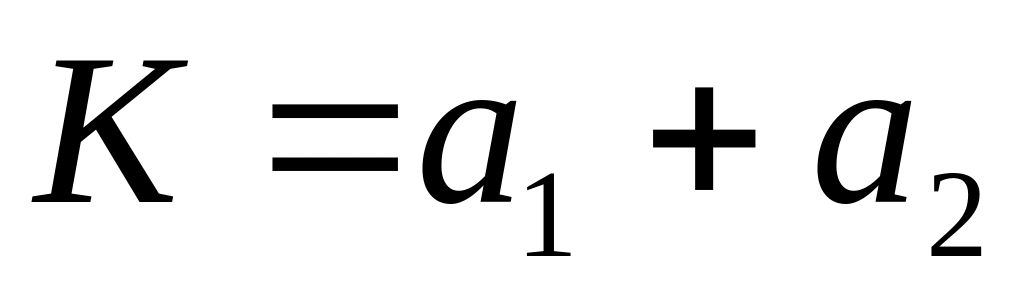14. Для побудови ізокванти задаємо довільне значення показника 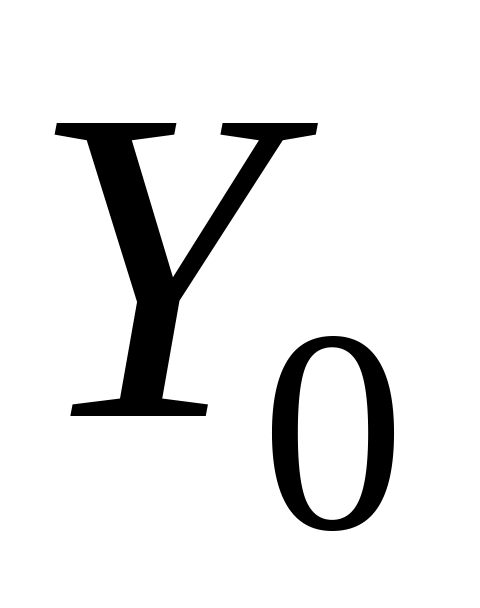, далі маємо рівняння ізокванти: 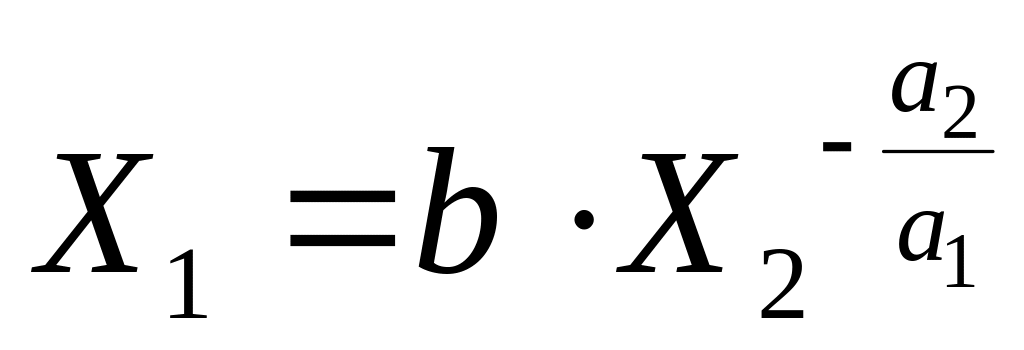, де ,

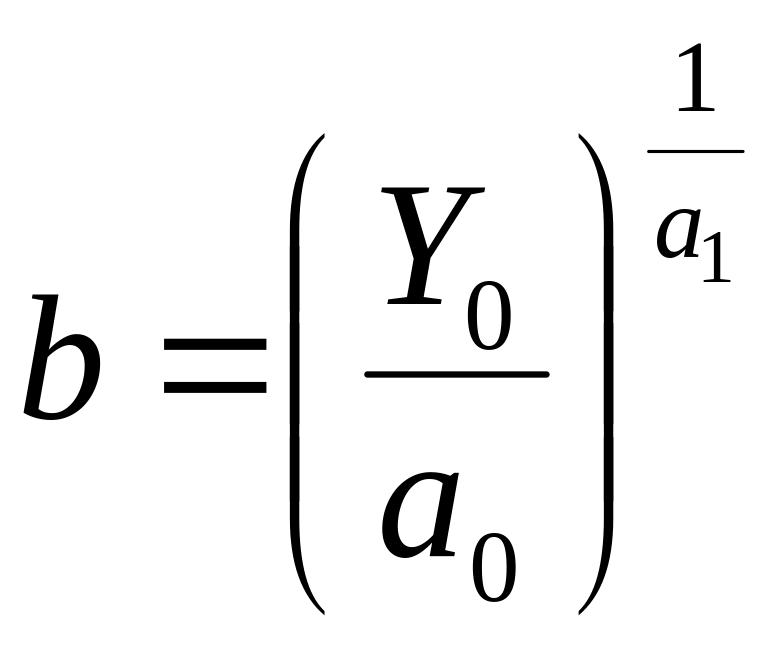Вважаємо, що в парі – впливова змінна.

15. Знайдемо значення для декількох послідовних значень : .

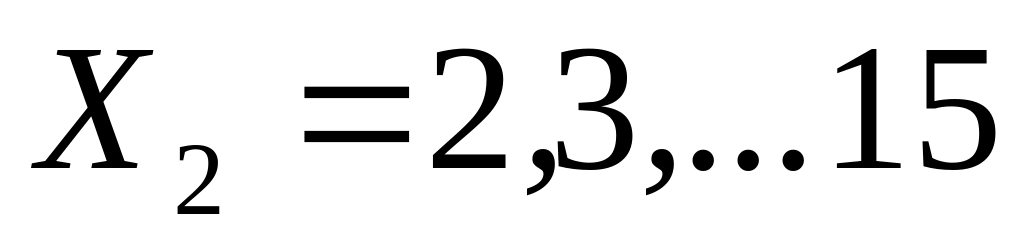16. Зобразимо отримані точ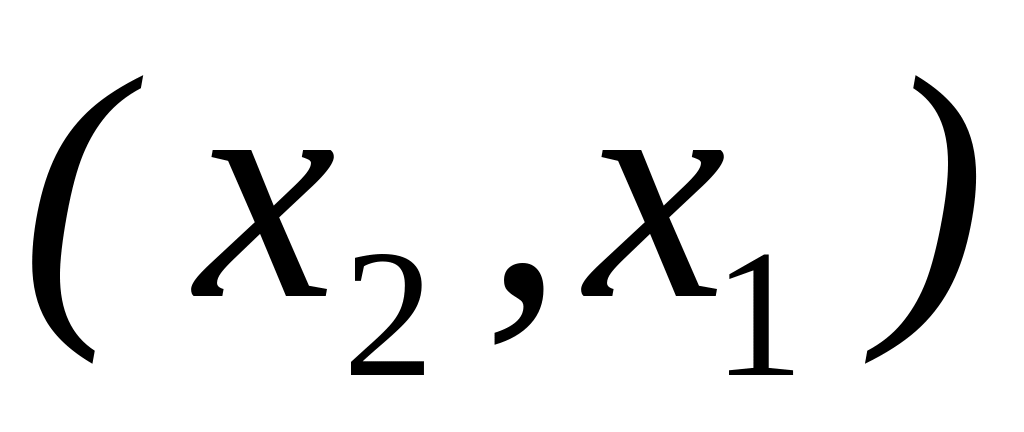ки на координатній площині, отримана крива і є графіком ізокванти для заданого значення показника (див. рис. 6.2). Зробити відповідні висновки.