Задания для решения в аудитории

1. Привести к каноническому виду задачу линейного программирования

, , .

1.2.2. Переход от канонической формы задачи линейного программирования к стандартной форме

Переход от канонической формы к стандартной форме задачи линейного программирования можно выполнить по следующему правилу:

1. Из коэффициентов при неизвестных и свободных членов уравнений системы ограничений и целевой функции составляется матрица. Коэффициенты целевой функции записываются в последнюю строку матрицы, на месте свободного члена записывается ноль.

2. Методом Жордана - Гаусса матрица приводится к разрешенному виду. При вычислениях разрешающий элемент в последней строке выбирать нельзя.

3. Составляется система уравнений из полученной разрешенной матрицы.

4. Базисные переменные в системе ограничений отбрасываются. При этом если переменная входила в уравнение со знаком , то в соответствующем уравнении ставится знак , если со знаком , то ставится знак .

5. Если целевая функция на максимум, то в системе ограничений все неравенства со знаком умножить на , если на минимум, то умножить неравенства со знаком .

Пример 4. Привести к стандартному виду задачу линейного программирования.

, , .

Решение. Из системы ограничений и целевой функции составим расширенную матрицу. Для наглядности запишем матрицу в виде таблицы.

Строки
	-1	1	2	-1	2
	9	-1	-6	5	6
	2	-1	2	1	0

Методом Жордана - Гаусса приведем полученную матрицу к разрешенному виду. Для этого выберем в первой строке разрешающий элемент, например . Выполним действия и .

Строки
	-1	1	2	-1	2
	8	0	-4	4	8
	1	0	4	0	2

Разделим всю вторую строку на .

Строки
	-1	1	2	-1	2
	-2	0	1	-1	-2
	1	0	4	0	2

Выберем во второй строке разрешающий элемент, например . Выполним действия и .

Строки
	3	1	0	1	6
	-2	0	1	-1	-2
	9	0	0	4	10

Составим из полученной матрицы систему ограничений и целевую функцию. При этом цифру из правого нижнего угла таблицы записываем с противоположным знаком в целевую функцию.

, , .

Разрешающие переменные входят в систему ограничений со знаком , значит их можно отбросить, а знак заменить на знак .

Стандартный вид исходной задачи:

, , .

Задания для решения в аудитории

1. Привести к стандартному виду задачу линейного программирования.

, , .

Задания для самостоятельной подготовки

1. Привести к каноническому виду задачу линейного программирования.

, , .

2. Привести к стандартному виду задачу линейного программирования.

, , .

1.3. Графический метод решения задач линейного программирования

1.3.1. Графический метод решения задач линейного программирования с двумя переменными

Рассмотрим стандартную задачу линейного программирования с двумя переменными:

, .

Допустимым решением задачи линейного программирования называется - мерный вектор , удовлетворяющий системе ограничений и условиям неотрицательности.

Множество допустимых решений образуют область допустимых решений задачи линейного программирования.

Оптимальным решением задачи линейного программирования называется допустимое решение, при котором целевая функция задачи принимает экстремальное значение ( или )

Для графического метода решения задач линейного программирования используются линии уровня целевой функции.

Линиями уровня функции называются прямые вида , которые параллельны между собой и перпендикулярны общему вектору нормали .

Алгоритм решения задачи линейного программирования с двумя переменными графическим методом:

1. По системе ограничений строится область допустимых значений. Если область допустимых решений пустое множество, то задача решения не имеет.

2. Строится вектор с точкой приложения в начале координат. Это вектор указывает направление возрастания целевой функции.

3. Перпендикулярно вектору проводится одна из линий уровня, например линия уровня функции , имеющая общие точки с областью допустимых решений.

4. Линия уровня перемещается по направлению вектора для задач на максимум и в противоположном направлении относительно вектора для задач на минимум до крайнего положения на области допустимых значений.

5. После нахождения оптимальных решений вычисляется значение целевой функции на этом решении.

В зависимости от вида области допустимых решений и линейной функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.

а) мин. знач. в точке А б) минимальное значение принимает на в) не ограничена в

макс. знач. в точке С опорной прямой, совпадающей с сторону увеличения

одной из сторон многоугольника значения мин. функции

Пример 5. Решить задачу линейного программирования графическим методом.

, .

Решение. Строим область допустимых решений.

1) Рассмотрим первое неравенство системы ограничений. Заменим знак неравенства знаком равенства и выразим из полученного уравнения одну из переменных, например : , . Для построения прямой достаточно двух точек: . Отмечаем эти две точки, проводим прямую и нумеруем ее цифрой один. Эта прямая разбивает всю плоскость на две части. Возьмем любую точку, не лежащую на этой прямой, и подставим ее координаты в первое неравенство. Например, возьмем точку (0;0). При подстановке координат этой точки в первое неравенство системы ограничений неравенство выполняется. Таким образом, стрелки на концах прямой направляются в сторону полуплоскости, содержащей выбранную точку.

Аналогично все остальные неравенства заменяем на равенства, строим соответствующие прямые и определяем полуплоскость решений.

2) , , .

3) , .

4) , - прямая параллельная оси абсцисс.

5) Находим общую часть полуплоскостей решений, учитывая условия неотрицательности.

6) Строим вектор нормали (координаты - коэффициенты целевой функции).

7) Через начало координат проводим линию уровня и, так как задача на отыскание максимума, двигаем ее по направлению вектора нормали до окончания области допустимых решений.

8) Крайней точкой области допустимых решений является точка пересечения прямых (2) и (4). Находим координаты этой точки, приравнивая уравнения прямых: .

9) Находим оптимальное значение целевой функции .

Пример 5. Решить задачу линейного программирования графическим методом.

, .

Решение. Строим область допустимых решений.

1) 4 , .

2) , .

3) , , .

4) - прямая параллельная оси ординат.

5) , .

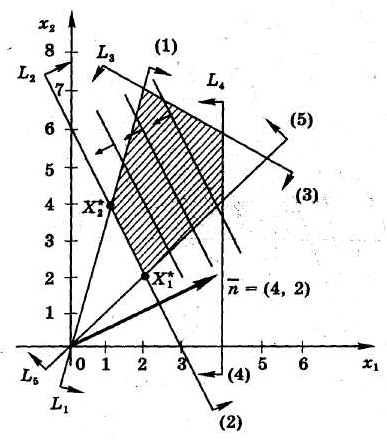
6) Находим общую часть полуплоскостей решений, учитывая условия неотрицательности.

7) Строим вектор нормали (координаты - коэффициенты целевой функции).

8) Так как задача на отыскание минимума, то линию уровня двигаем против направления вектора нормали до окончания области допустимых решений.

9) Крайним положением линии уровня является прямая (2). Она проходит через точки (пересечение прямых (1) и (2)) и (пересечение прямых (5) и (2)). В таком случае задача имеет бесконечное множество решений, расположенных на отрезке .

10) Решаем системы и и находим точки и .

10) Находим оптимальное значение целевой функции .