9.Кольца, их основные свойства. Кольца многочленов, их свойства. Подкольца, идеалы, их свойства. Поля, их основные свойства.

Кольцом называется множество K с бинарными операциями "+" и "", для которых выполнены три следующих условия:

a) K – абелева группа относительно операции "+";

b) операция "" ассоциативна;

c) выполняются законы дистрибутивности, т. е.

.

Единица аддитивной группы кольца K называется нулем и обозначается символом 0. Кольцо называется:

a) кольцом с единицей, если оно имеет мультипликативную единицу;

b) коммутативным, если операция "" – коммутативна;

c) целостным кольцом (областью целостности), если оно является коммутативным кольцом с единицей , в котором равенство влечет за собой или ;

d) телом, если и ненулевые элементы образуют группу относительно операции "", а коммутативное тело называется полем.

Например, a) целые числа образуют целостное кольцо, но не поле; b) четные числа образуют кольцо без единицы; c) множество всех квадратных матриц порядка n образует некоммутативное кольцо с единицей относительно операций сложения и умножения матриц.

Если K – произвольное кольцо, то многочленом или полиномом над K называется выражение вида

,

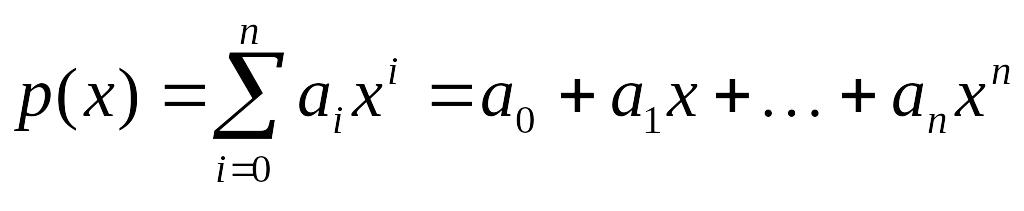где n – неотрицательное целое число, коэффициенты , а x – некоторый символ (переменная над K), не принадлежащий кольцу K.

Многочлены

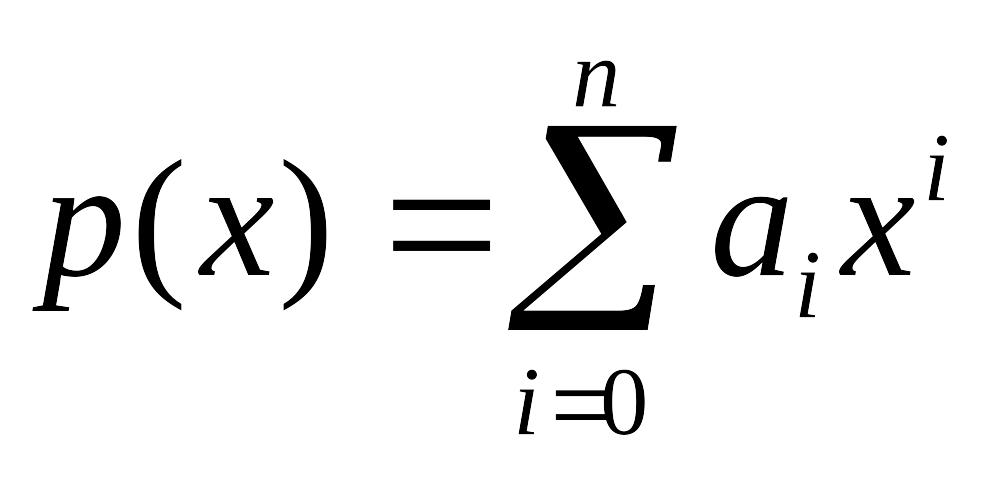и

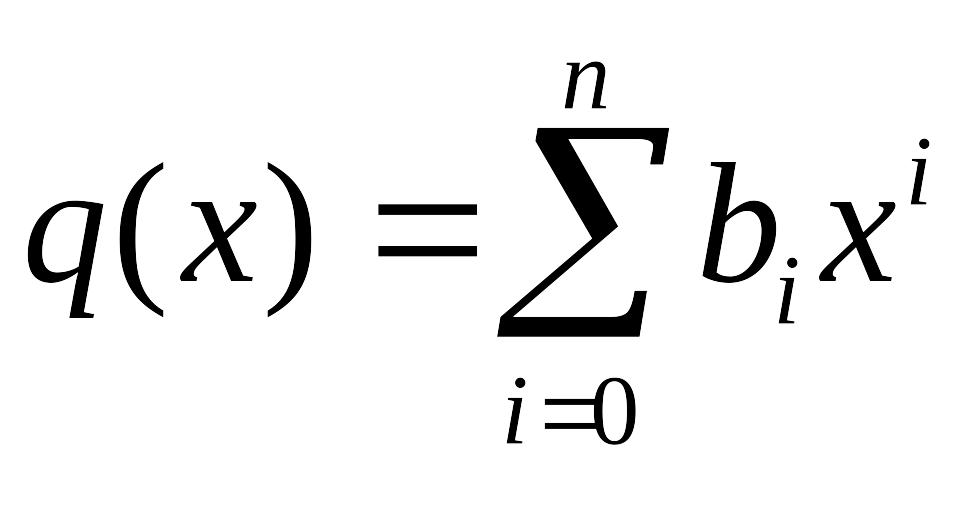
над K считаются равными, если . Сумма многочленов и определяется равенством

,

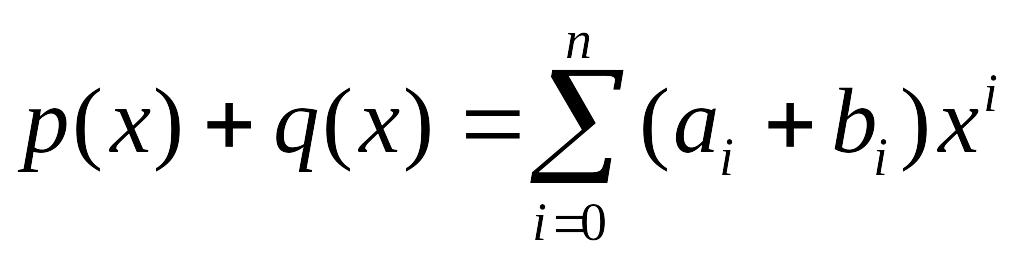а произведение многочленов

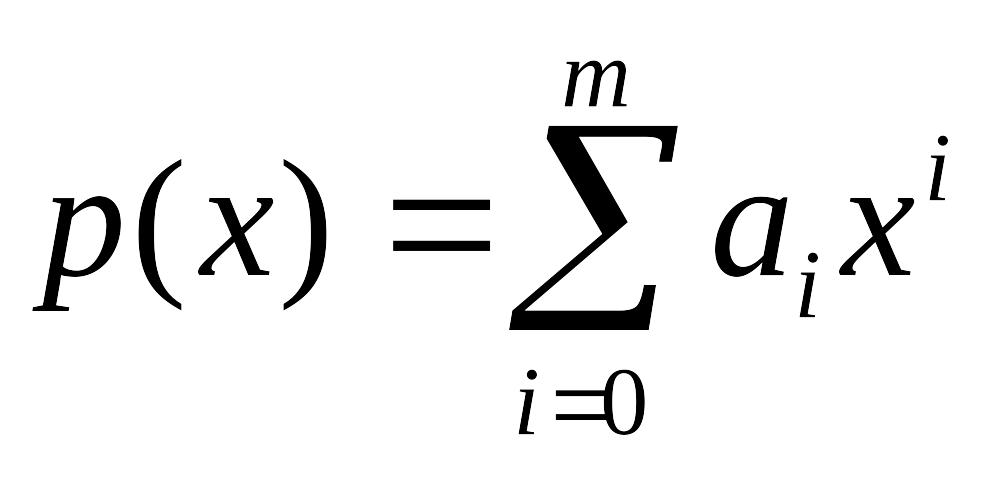и

определяется соотношением

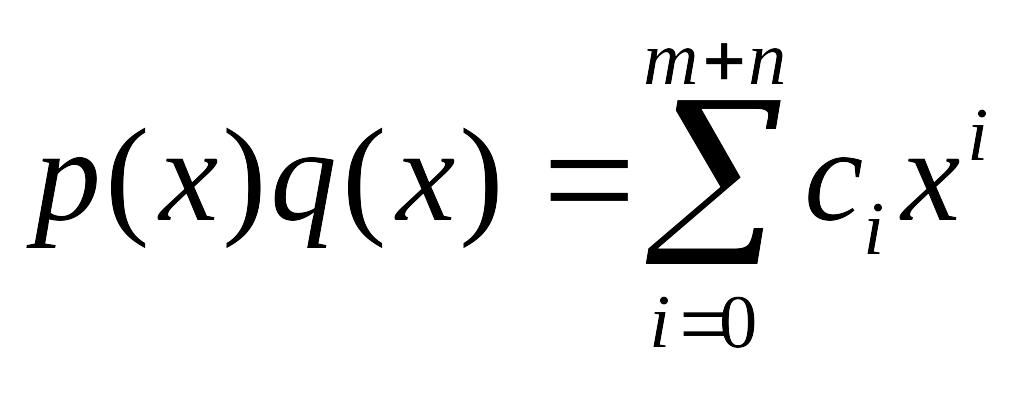, где .

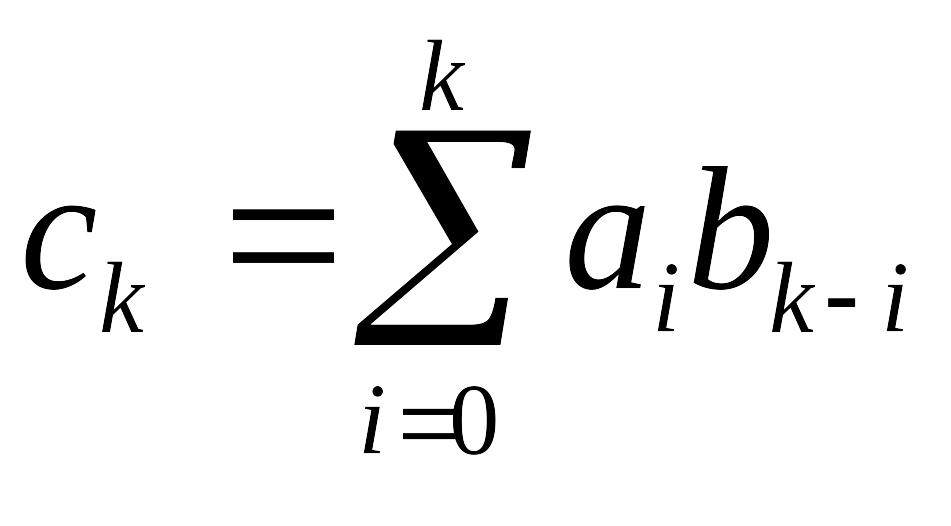Кольцо многочленов, образованное введенными операциями, называется кольцом многочленов над K и обозначается .

Для многочлена коэффициент называется старшим коэффициентом,  – его постоянным членом, а n – его степенью. Степень многочлена обозначается , причем полагают . Многочлены степени называются константами. Если кольцо K имеет единицу и если старший коэффициент многочлена равен 1, то этот многочлен называется нормированным, а также приведенным или унитарным.

Подмножество J кольца называется подкольцом, если оно замкнуто относительно операций "+" и "" и образует относительно них кольцо.

Подкольцо J кольца K называется (двусторонним) идеалом этого кольца, если и имеет место и .

Идеал J коммутативного кольца K называется главным идеалом, порожденным элементом a, если , такой, что .

Идеалы в теории колец играют роль, аналогичную роли нормальных групп в теории групп. Так как идеалы являются нормальными подгруппами аддитивной группы кольца, то каждый идеал J кольца K определяет некоторое разбиение множества K на смежные классы по аддитивной группе J, называемые классами вычетов кольца K по модулю идеала J.

Полем называют множество элементов, на котором определены две операции. Одна из них называется сложением и обозначается a+b, а другая – умножением и обозначается a · b, даже если эти операции не являются обычными операциями сложения и умножения чисел. Для того чтобы множество элементов, на котором заданы операции сложения и умножения, было полем, необходимо, чтобы по каждой из этих операций выполнялись все групповые аксиомы (ассоциативно,сущ-ет единица, обр.эл-т), а также выполнялся дистрибутивный и коммуникативный законы:

1) а · (b+с) = а · b+а · с и (b+с) · а = b · а+с · а

2) а + b = b + a и а · b = b · а