5.Отношение эквивалентности и его свойства. Отношение порядка и его свойства. Матричное представление отношений.

Отношением эквивалентности или просто эквивалентностью на X называется отношение R, обладающее свойствами рефлексивности, симметричности и транзитивности. Вместо часто пишут . Подмножество называется классом эквивалентности элемента x по модулю R. Множество X является дизъюнктным объединением этих классов, а множество всех классов эквивалентности называется фактормножеством множества X по модулю R и обозначается .

Подмножество T из X, содержащее в точности по одному элементу из каждого R-класса, называется трансверсалом множества X по модулю R.

Антисимметричное транзитивное отношение R называется отношением порядка. Если выполняется свойство рефлексивности или антирефлексивности, то оно соответственно называется отношением нестрого или строго порядка. Если отношение порядка обладает свойством полноты (линейности), то оно называется отношением полного (линейного) порядка. В противном случае оно называется отношением частичного порядка.

Обычно отношение строго порядка обозначается знаком <, а отношение нестрого порядка – знаком . В общем случае для обозначения отношения порядка используется знак .

Отношение при после соответствующей нумерации элементов множества X можно представить матрицей R, элементы которой определяются следующим образом:

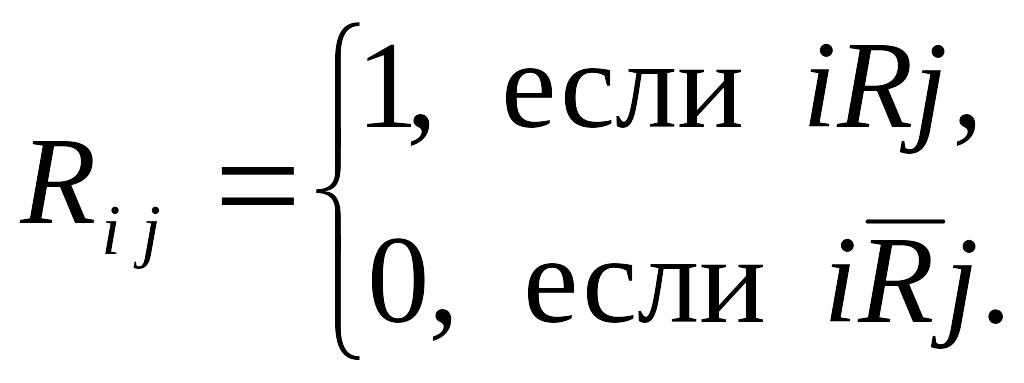
6.Функции, их свойства. Представление функций в эвм. Инъекция, сюръекция и биекция, их свойства.

Отношение , обладающее свойством однозначности

называется (однозначной) функцией (отображением). Функция обозначается следующим образом: или . Также используется запись: или , где x называется аргументом, а y – значением функции.

Наиболее общим представлением функции в ЭВМ является ее запись в виде двумерного массива. Функция m-переменных представляется в виде -мерного массива.

Для представления функций в ЭВМ также используется особый вид процедур, возвращающих единственное значение для данного аргумента.

Для функции область определения , образ (область значений) и ядро определяются соотношениями:

,

.

Функция называется:

инъективной, если ;

сюръективной, если ;

биективной, если она инъективна и сюръективна.

Биективную функцию также называют взаимнооднозначной.

Для конечных множеств X и Y классы инъективных, сюръективных и биетивных функций непусты, если соответственно выполнены соотношения: , и .

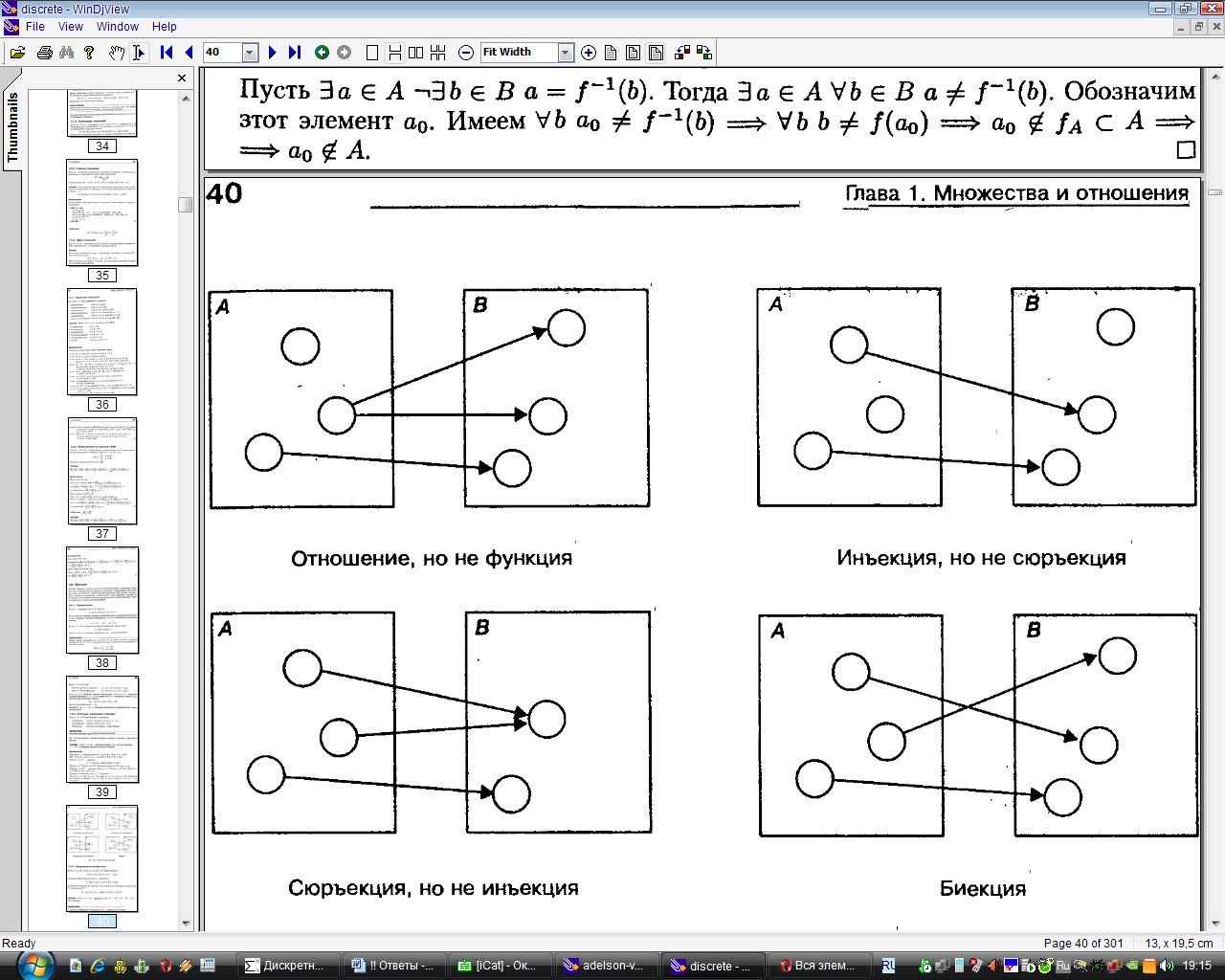
Представление функций в ЭВМ

Наиболее общим представлением функции в ЭВМ является ее запись в виде двумерного массива. Пусть f: А →В, множество А конечно и не очень велико, |A| = n. Наибо­лее общим представлением такой функции является массив array [A] of В

7.Подстановки, перестановки, группы подстановок. Представление подстановок циклами.

Важным примером биективной функции является биективное отображение n-множества X на себя, которое называется подстановкой (на множестве X).

Подстановкой называется множество равенств

s={x1=t1, x2=t2,…, xn=tn},

где x1,x2,…,xn – различные переменные, t1,t2,…,tn – термы.

Перестановкой из n элементов называются размещения, в которых участвуют все элементы множества Pn

Pn=n!

Множество G подстановок, замкнутое относительно выполнения операции композиции и содержащее тождественную (единичную) подстановку e и обратную подстановку ( , где умножение обозначает операцию композиции) называется группой.

Отображение

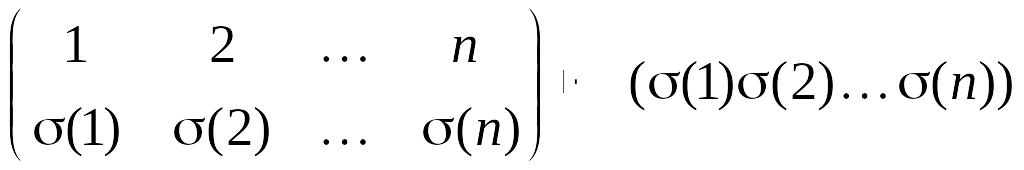
задает канонический изоморфизм двух групп – группы подстановок  на множестве X и группы перестановок  на множестве X. Перестановку  можно рассматривать как n-набор или как n-слово .

Группу всех подстановок (перестановок) называют симметрической группой и обозначают , а число переставляемых элементов n называется степенью группы. Число элементов в конечной группе называется ее порядком. Для симметрической группы порядок равен n!.

Другим общепринятым способом представления подстановок (перестановок) является их запись в виде объединения (произведения) циклов

.

Каждый элемент подстановки встречается в единственном цикле. Порядок записи циклов не имеет значения, а цикл может начинаться с любого своего элемента. Длина цикла  – это количество элементов, содержащихся в нем. Циклы длины 1 называются тривиальными и соответствуют неподвижным элементам , их часто опускают при записи произведения.

Если подстановка имеет единичных циклов, двойных циклов и. т. д., то она называется подстановкой циклового класса .

Тот же самый смысл имеет обозначение , принятое в теории разбиений, причем справедливо равенство .

Если обозначить число подстановок , имеющих в точности k циклов, то число известно как число Стирлинга первого рода, причем называют числом Стирлинга первого рода без знака.

Если в единичной перестановке поменять местами i-й и j-й элементы, то такая перестановка называется транспозицией. Каждую перестановку можно многими способами представить в виде произведения транспозиций. Четность перестановки совпадает с четностью ее разложения в произведение транспозиций, что легко доказывается по индукции. В группе можно выделить подгруппы четных и нечетных перестановок.

Пара называется инверсией перестановки , если при имеем . Число инверсий перестановки  обозначается через . Если четно, то перестановка  является четной и ей присваивается знак "+"; если нечетно, то перестановка  является нечетной и ей присваивается знак "–". Таким образом, .