52.Марковский процесс с дискретными состояниями и непрерывным временем.

Имеется система S, которая в каждый момент времени может находиться в одном из состояний S₁, S₂, …,S_n. Переход системы из одного состояния в другое может осуществляться в любой момент времени. Такой процесс называется непрерывной цепью Маркова.

Обозначим p_i(t) –вероятность того, что в момент времени t система S будет находиться в состоянии S_i (i=1,2,…,n). Для любого момента времени

.

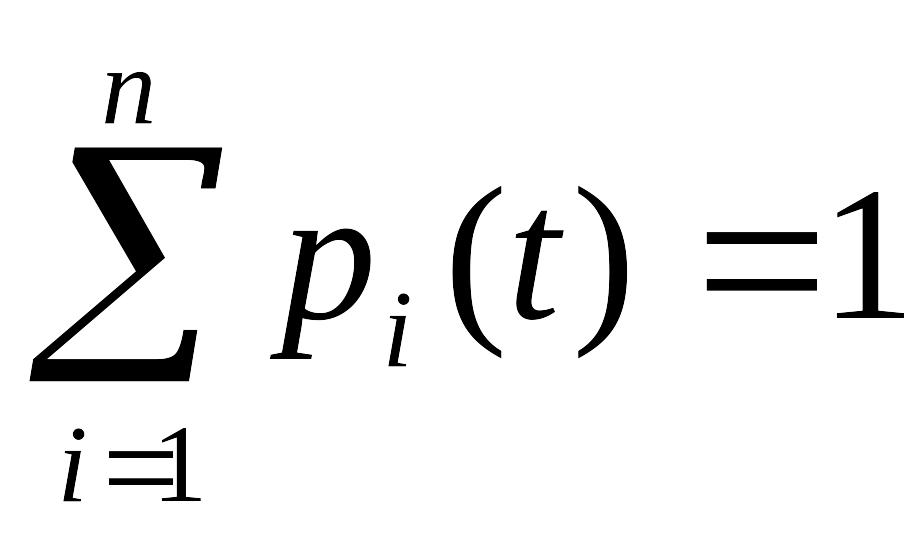Поставим задачу – определить для любого t вероятность состояний: p₁(t), p₂(t), …,p_n(t). Будем считать, что известны плотности вероятностей перехода . Пусть - вероятность перехода системы S из состояния S_i в состояние S_j за время . Тогда

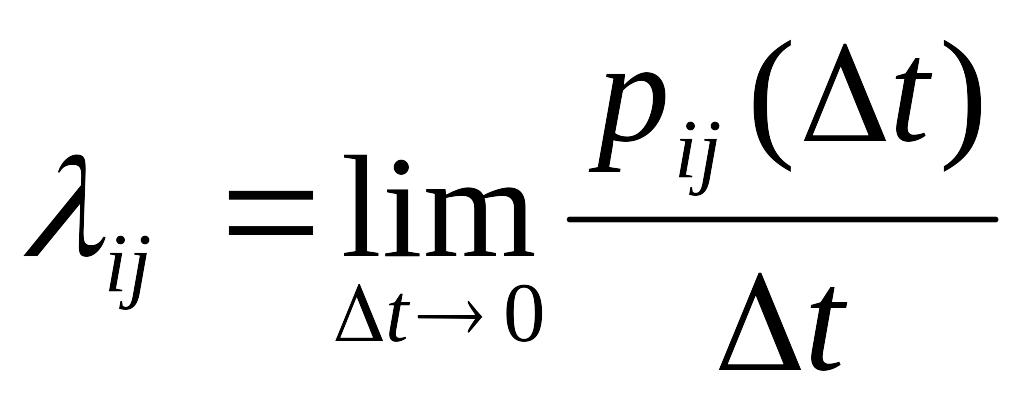
Тогда с точностью до бесконечно малых высших порядков

Если не зависят от t, Марковский процесс называется однородным, если зависят – то неоднородным. Вероятности удовлетворяют следующей системе дифференциальных уравнений:

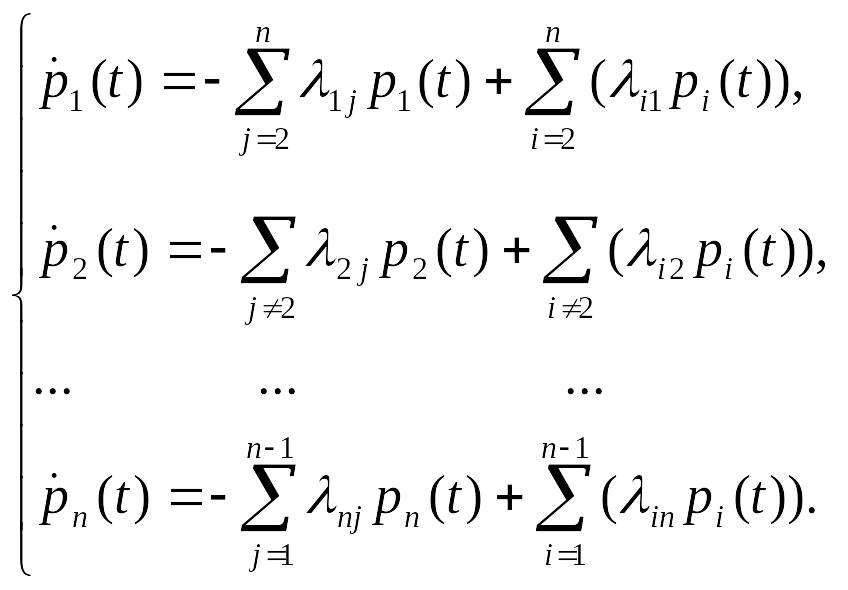
Эти уравнения для вероятностей состояний называются уравнениями Колмогорова. Для однозначного решения системы должны быть заданы начальные значения: p₁(0), p₂(0), …,p_n(0), причем

Предположим, что

где p_i финальные вероятности. Чтобы их найти в системе положим . Тогда будем иметь следующую систему линейных алгебраических уравнений

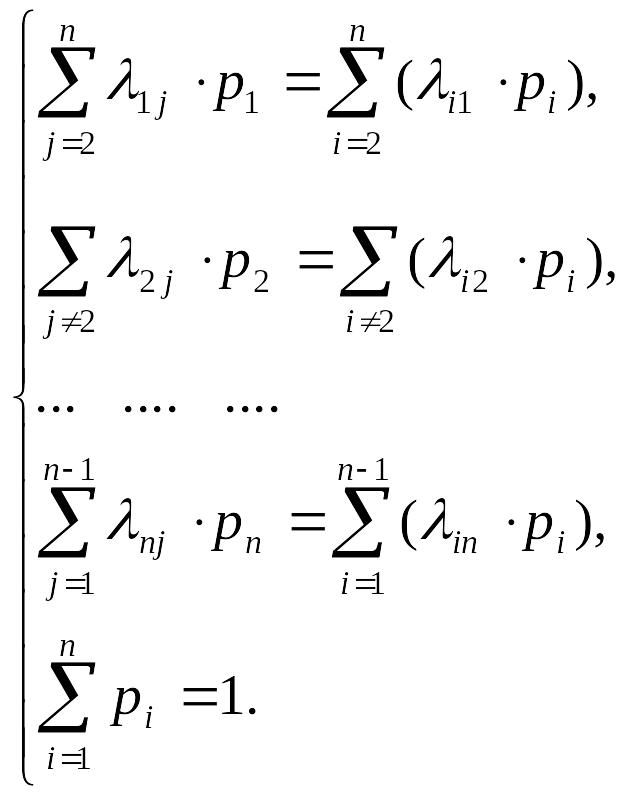. (7)

Здесь n+1 уравнение с n неизвестными. Поэтому одно из однородных уравнений можно отбросить.

53.Система массового обслуживания с отказами.

В таких системах заявка, поступившая в момент, когда все каналы заняты, немедленно получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует.

Пусть имеется n канальная система массового обслуживания с отказами. Рассмотрим ее как физическую систему Х с конечным множеством состояний:

x₀ – свободны все каналы,

x₁ – занят ровно один канал,

……………………………..

x_n – заняты все n каналов.

Требуется определить вероятности состояний системы (k=0,1,2,…,n) для любого момента времени t. Задачу решить при следующих допущениях:

1). Поток заявок – простейший с плотностью ;

2). Время обслуживания Т_об - показательное с параметром

Процесс, протекающий в системе, будет Марковским.

Вероятности удовлетворяют следующим уравнениям Эрланга:

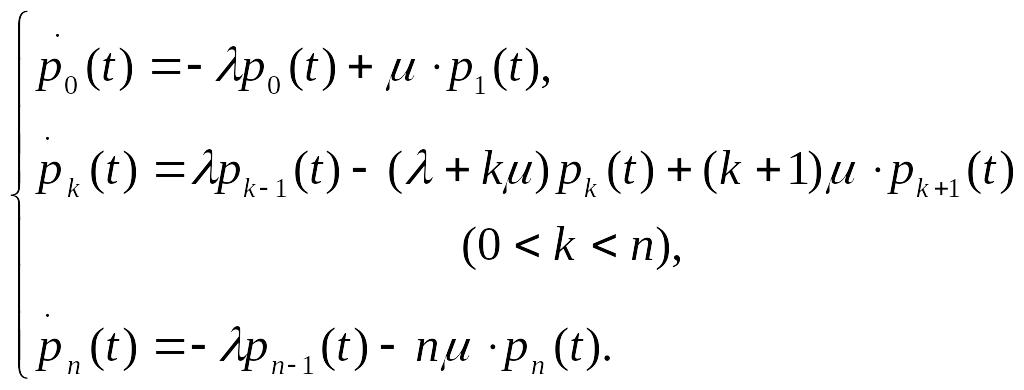
Для любого момента времени должно выполняться условие

Вероятность характеризует среднюю загрузку системы и ее изменение с течением времени.

Величина называется относительной пропускной способностью системы. Для данного момента t это есть отношение среднего числа обслуженных за единицу времени заявок к среднему числу поданных.

54.Система массового обслуживания с ограничением по длине очереди.

(Система массового обслуживания смешанного типа)

Рассмотрим смешанную систему массового обслуживания Х с n каналами при следующих условиях. На вход системы поступает простейший поток заявок с плотностью . Время обслуживания одной заявки Т_об - показательное с параметром . Заявка, заставшая все каналы занятыми, становится в очередь и ожидает обслуживания при условии, что длина очереди меньше m. Если же число заявок в очереди равна m (больше m оно быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему не обслуженной.

Заявку будем называть «связанной с системой», если она либо находится в состоянии обслуживания, либо ожидает очереди. Возможные состояния будут

x₀ – ни один канал не занят,

x_k – занято ровно k каналов (1 x n) ,

x_n+s – заняты все n каналов. s заявок стоят в очереди. (1 ≤ s ≤ m).

Число заявок s, стоящих в очереди, не может быть больше m. Соответственно, число описывающих ее дифференциальных уравнений равно n+m+1. Они имеют вид:

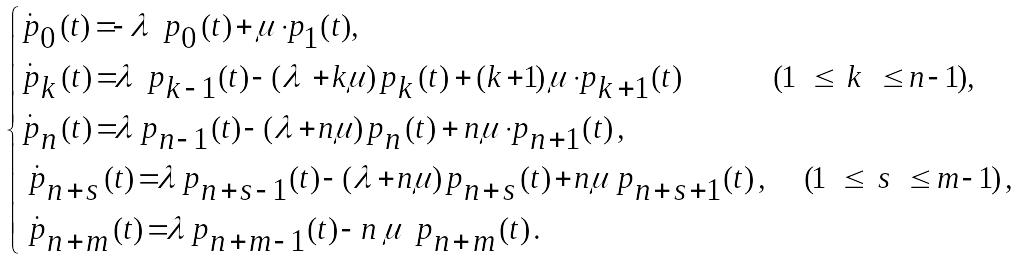(2)

Н ачальными условиями являются:

Вероятность того, что заявка покинет систему необслуженной, равна p_n+m. Относительная пропускная способность системы определяется формулой

.