50.Игры 2 на n и m на 2.

В играх порядка 2 x m первый игрок имеет две стратегии, а второй – m стратегий. Платежная матрица имеет вид:

| a11 a12 … a1m |

A= | a21 a22 … a2m |

Причем у нее нет седловых точек.

Необходимо найти такие смешанные стратегии x=S1=(p1*p2) и S2=q1, … ,qm и цену игры gamma, которые удовлетворяют соотношениям

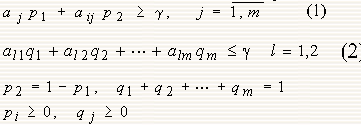
Что означают неравенства (1) и (2). Пусть игрок 1 применяет свою оптимальную стратегию S1* а его противник применяет чистую стратегию yj . Т.к. это цена игры gamma, то она определяет нижний придел выигрыша при любых стратегиях второго игрока, в том числе смешанных. Аналогично можно объяснить неравенство (2) – верхний предел проигрыша 2-го игрока. Не доказывая, отметим, что любая конечная игра m x n имеет решение, в котором число активных стратегий каждого игрока не превосходит min(m,n) .Следовательно, у игры 2 x m или n x 2 всегда имеется решение, содержащее не более двух активных стратегий у каждого из игроков. Если найти эти активные стратегии игроков, то игра 2 x m или n x 2 превращается в игру 2x2 .

Введем обозначение для левой части неравенств (1)

Mj(p1) = a1j*p1 + a2j *p2 = a1j*p1 + a2j(1-p1)=(a1j-a2j)*p1+a2j j=1,m , где Mj(p1) – средний выигрыш первого игрока при условии, что он применяет свою смешанную стратегию, а второй – свою j чистую стратегию. Каждому значению j=1,m соответствует прямая линия прямоугольной системы координат.

Цель второго игрока минимизировать выигрыш первого за счет своих альтернатив. Поэтому 2 игрок должен определить такие j, которые обеспечивают min Mj(p1) = M(p1), где M(p1) – нижняя граница множества ограничений (показана жирной линий).

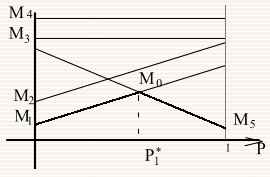
Цель первого игрока максимизировать свой выигрыш за счет выбора p1 , т.е. вычислить max M(p1)=gamma.

В результате определяется оптимальная стратегия первого игрока S1*=(p1*,1-p1*) и пара альтернативных стратегий 2 игрока, которые при пересечение образуют точку M0 . В нашем случае это y1 и y5 . В результате мы свели задачу размерности 2 x m , к задаче 2 x 2 с платежной матрицей

| a11 a15 |

A= | a21 a25 |

Решая полученную игру найдем S1*=(p1*,p2*) и S1*=(q1*,q2*)

51.Марковский процесс с дискретными состояниями и дискретным временем

Случайный процесс называется процессом с дискретным временем, если переходы системы S из состояния в состояние возможны только в строго определенные моменты времени t₁, t₂,…. В промежутки времени между этими моментами система сохраняет свое состояние.

Процесс, происходящий в системе, можно представить как последовательность событий, например: Такая случайная последовательность событий называется марковской цепью.

Мы будем описывать марковскую цепь с помощью так называемых вероятностей состояний. Пусть после k-ого шага система S может быть в одном из состояний S₁, S₂, …,S_n, т.е. осуществится одно из полной группы несовместных событий: .

Обозначим вероятности этих событий:

(короче: вероятность того, что после k-го шага система перейдёт в m-е состояние равна вероятности m-го события на k-м шаге)

Будем называть вероятности вероятностями состояний. Найдем эти вероятности для любого k.

Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага. В противном случае марковская цепь называется неоднородной.

Обозначим p_ij вероятность перехода системы S за один шаг из состояния S_i в состояние S_j. Эти вероятности можно записать как условные вероятности p_ij.

Из вероятностей p_ij можно составить матрицу

,

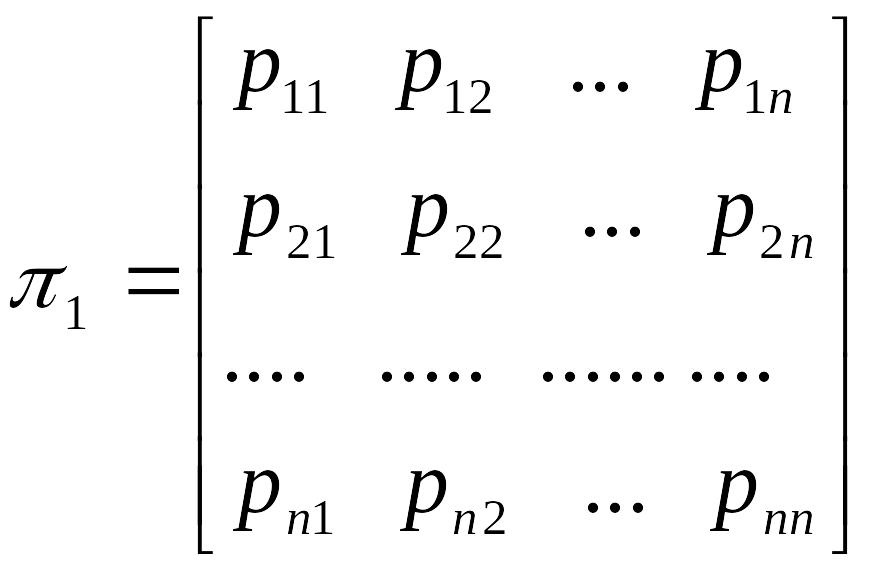которая называется матрицей перехода за один шаг. Сумма элементов каждой строки равна единице.

Обозначим p_ij(k) вероятность перехода системы S из состояния S_i в состояние S_j за k шагов. Обозначим через _k матрицу перехода через k шагов

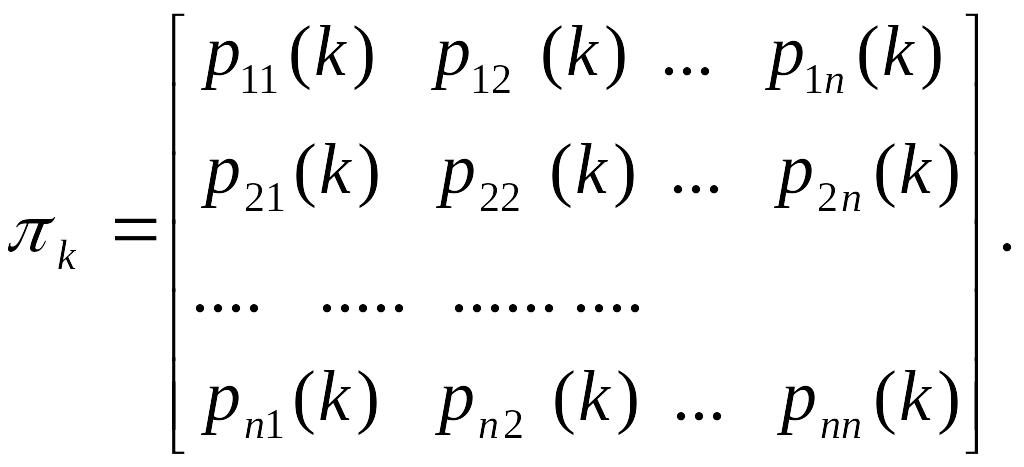
Согласно между матрицами перехода с различными индексами существует соотношение _k =_l _k-l (0<l<k). В частности, при k=2 находим, что при k=3 и вообще при любом k

Теорема Маркова. Если при некотором S>0 все элементы матрицы положительны, то существуют такие постоянные числа p_j (j=1,2,3,…,n) что независимо от индекса i имеют место равенства

Величины p_j называются финальными вероятностями системы S.