46.Платежная матрица. Нижняя и верхняя цена игры. Принцип минимакса.

Множество, образованное всеми упорядоченными параметрами (x, y) первый член которых и есть элемент из X, а второй член – элемент из Y называется прямым или декартовым произведением множеств X и Y.

Система, где X и Y – непустые множества, функция называется антагонистической игрой в нормальной форме.

Элементы и называются стратегиями игроков 1 и 2 соответственно в игре, элементы декартова произведения (пары стратегий (x, y)) называются ситуациями , функция K(x, y) – функция выигрыша игрока 1. Выигрыш игрока 2 в ситуации (x, y) полагается равным [–K(x, y)]. Такая игра называется игрой с нулевой суммой.

Правила игры можно записать в виде таблицы

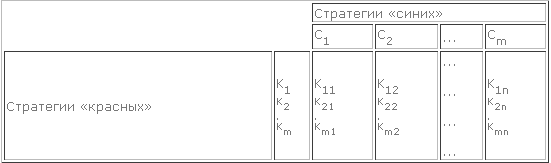
(или матрицы), в которой m строк и n столбцов. Строки соответствуют стратегиям «красных», которые мы обозначим:K1, K2, ..., Km, а столбцы — стратегиям «синих»: C1, C2, ..., Cn. В клетках таблицы помещены выигрыши (или средние выигрыши) «красных» при соответствующей паре стратегий. Например, k12 — выигрыш, который получат «красные», если вы берут стратегию K1, а «синие» — С2; вообще, kij — выигрыш «красных» при комбинации стратегии Ki и Cj. Такая таблица называется платежной матрицей или просто матрицей игры.

Если конечная игра записана в виде такой матрицы, то говорят, что она приведена к нормальной форме. Игра называется игрой с нулевой суммой, если одна сторона выигрывает то, что проигрывает другая. Если оба игрока придерживаются оптимальных стратегий, то устанавливается средний оптимальный выигрыш – цена игры. Если цена игры равна нулю, значит, это справедливая игра, т. е. она в одинаковой мере выгодна или невыгодна той и другой стороне Если цена игры положительна, значит игра выгодна для К, если отрицательна, то выгодна другой стороне.

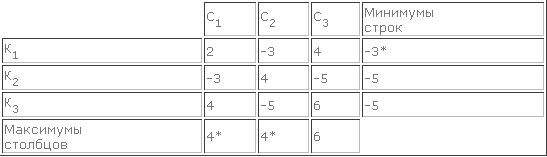
Максимин (нижняя цена игры) – максимальное значение среди минимумов каждой строки (-3 см рисунок)

Минимакс (верхняя цена игры) – минимальное значение среди максимумов каждой строки (4 см рисунок)

Max j min i aij = min j max i aij равенство является принципом минимакса

Принцип минимакса: в игре веди себя так, чтобы получить наибольшую выгоду при наихудших для тебя действиях противника.

47.Решение игры в смешанных стратегиях.

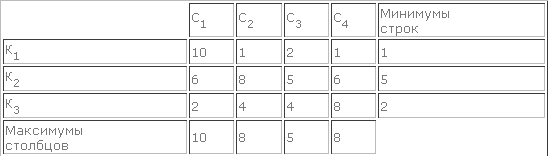
Если есть элемент минимальным в своей строке и одновременно максимальным в своем столбце.( это 5) Такой элемент называется седловой точкой(т. е. нижняя цена игры равна верхней) то игра имеет решение в чистых стратегиях: это — пара стратегий, пересекающихся в седловой точке. Сама же седловая точка дает цену игры — в нашем примере она равна 5.

А если α ≠ β, то решение лежит в области смешанных стратегий

Смешанные стратегии – полный набор вероятностей применения его чистых стратегий

х1 + х2 = 1, х1 ≥ 0, х2 ≥ 0, (5.10)

у1 + у2 = 1, у1 ≥ 0, у2 ≥ 0. (5.11)

Точки х = (х1, х2) и у = (у1, у2), отвечающие условиями (5.10) и (5.11), назовем смешанными стратегиями первого и второго игрока. Множества смешанных стратегий обозначим Х и Y, они станут отрезками прямых на координатных плоскостях переменных х1, х2 и у1, у2, и функция. Значения функции Н(х, у) будем трактовать как «частоты» выбора чистых стратегий и как «средние» выигрыши.

Н(х, у) ≡ Н(х1, х2, у1, у2)

Смешанные стратегии х*, у* назовем оптимальными в игре Г, если для любых стратегий х, у выполнены неравенства

Н (х, у*) ≤ Н (х*, у*) ≤ Н (х*, у). (5.12)

Левое неравенство (5.12) показывает, что стратегия х = х* в ситуациях (х, у*) обеспечивает первому игроку наибольший «средний» выигрыш Н(х*, у*). Правое неравенство означает, что в ситуациях (х*, у) стратегия у = у* гарантирует второму игроку минимальный проигрыш Н(х*, у*). В этом смысле стратегии х*, у* являются для игроков наилучшими.

Основная теорема теории игр: Решением игры называется такая пара стратегий — в общем случае смешанных, систематическое применение которых обеспечивает каждой стороне максимально возможный для нее по условиям игры выигрыш, определяемый ценой игры. Если же одна из сторон отступает от своей оптимальной стратегии (в то время как другая продолжает придерживаться своей), то это ни в коем случае не может быть выгодно для отступающего; это либо оставит его выигрыш неизменным, либо уменьшит.