
- •1.Множества, подмножества. Операции над множествами и их свойства. Диаграммы Эйлера – Венна
- •2.Покрытия и разбиения множеств. Биномиальные коэффициенты и числа Стирлинга второго рода. Перечисление элементов множеств.
- •3.Представление множеств в эвм. Коды Грея. Мультимножества.
- •4.Отношения и их основные свойства. Композиция отношений.
- •5.Отношение эквивалентности и его свойства. Отношение порядка и его свойства. Матричное представление отношений.
- •6.Функции, их свойства. Представление функций в эвм. Инъекция, сюръекция и биекция, их свойства.
- •7.Подстановки, перестановки, группы подстановок. Представление подстановок циклами.
- •8.Операции на алгебраических структурах. Группы, подгруппы, нормальные группы, их свойства.
- •9.Кольца, их основные свойства. Кольца многочленов, их свойства. Подкольца, идеалы, их свойства. Поля, их основные свойства.
- •10.Графы и орграфы. Простейшие типы графов. Представление отношений графами.
- •11.Матрицы смежности и инцидентности, их основные свойства. Смежностные (реберные) графы.
- •12.Изоморфизм графов.
- •13. Подграфы. Остовные подграфы. Операции на графах.
- •14. Компоненты графа, связность.
- •15.Маршруты, цепи, циклы. Диаметр, радиус и обхват графа. Пути в орграфах.
- •17.Теоремы существования эйлеровых и гамильтоновых циклов.
- •18.Задачи о кратчайшем пути.
- •19. Вершинные и реберные раскраски графа. Хроматический многочлен, хроматическое число и хроматический индекс.
- •20. Планарность. Формула Эйлера. Теорема Потрягина-Куратовского. Теорема о четырех красках.
- •21.Деревья. Матричная теорема о деревьях, подсчет числа остовов.
- •22.Корневые деревья. Задачи о подсчете корневых деревьев. Высота дерева. Числа Фибоначчи, их свойства.
- •23. Кубические деревья. Числа Каталана, их свойства.
- •24.Основные понятия булевой алгебры: булев куб, булевы функции.
- •25.Элементарные булевы функции, их свойства. Существенные и фиктивные переменные. Основные функциональные элементы.
- •26.Формулы. Реализация булевых функций формулами. Принцип двойственности.
- •27.Разложение булевых функций по переменным. Совершенная днф и совершенная кнф.
- •28. Полиномы Жегалкина. Не полностью определенные (частичные) булевы функции.
- •29.Виды днф и кнф: сокращенные, минимальные, кратчайшие, тупико-вые.
- •30. Методы построения сокращенных днф. Минимизация днф. Геометрическая интерпретация. Метод Блейка.
- •31.Метод минимизирующих карт (карт Карно). Реализация булевых функций схемами из функциональных элементов.
- •32. Полнота и замкнутость
- •33.Важнейшие замкнутые классы. Теорема о полноте. Примеры функционально полных базисов.
- •34. Основные понятия о разрешимых и неразрешимых проблемах. Алгоритмы и разрешимость.
- •35. Схемы алгоритмов, схемы потоков данных и использовании теории графов и теории конечных автоматов для их описания.
- •36.Формула полной вероятности.
- •37.Формула Бейеса.
- •38.Формула Бернулли.
- •39.Функция распределения, плотность распределения и их свойства. Связь между ними.
- •40.Числовые характеристики случайных величин.
- •41.Нормальное распределение.
- •42. Метод золотого сечения
- •43.Метод касательных.
- •44.Метод наискорейшего спуска.
- •45.Метод покоординатного спуска.
- •46.Платежная матрица. Нижняя и верхняя цена игры. Принцип минимакса.
- •47.Решение игры в смешанных стратегиях.
- •48.Упрощение игр.
- •49.Игра 2 на 2.
- •50.Игры 2 на n и m на 2.
- •51.Марковский процесс с дискретными состояниями и дискретным временем
- •52.Марковский процесс с дискретными состояниями и непрерывным временем.
- •53.Система массового обслуживания с отказами.
- •54.Система массового обслуживания с ограничением по длине очереди.
- •55.Исчисление высказываний
- •57.Логика предикатов первого порядка
44.Метод наискорейшего спуска.
Метод
применяется для нахождения минимума
некоторой функции
![]() = f(x1, x2, ..., xn), заданной в евклидовом
пространстве, где
= f(x1, x2, ..., xn), заданной в евклидовом
пространстве, где
![]() = (x1, x2, ..., xn) — вектор. Численные методы
отыскания экстремума функции
состоят в построении последовательности
векторов {
= (x1, x2, ..., xn) — вектор. Численные методы
отыскания экстремума функции
состоят в построении последовательности
векторов {![]() },
удовлетворяющих условию: f(
},
удовлетворяющих условию: f(![]() )
> f(
(1))
> ... > f(
)
> f(
(1))
> ... > f(![]() (n)).
Методы построения таких последовательностей
называются методами спуска. В этих
методах элементы последовательности
{
(n)).
Методы построения таких последовательностей
называются методами спуска. В этих
методах элементы последовательности
{![]() }
вычисляются по формуле
}
вычисляются по формуле
![]() (k
= 0,1,2,...…),
(k
= 0,1,2,...…),
где
вектор
![]() (k)
определяет направление спуска;
(k)
определяет направление спуска;
![]() — длина
шага в данном направлении.
— длина
шага в данном направлении.
Градиент функции в точке направлен в сторону наискорейшего локального возрастания функции. Следовательно, направление спуска должно быть противоположным градиенту. Вектор, противоположный градиенту, называется антиградиентом. Выбирая антиградиент в качестве направления спуска, приходят к итерационному процессу вида
![]() (k
= 0,1,2,...),
(k
= 0,1,2,...),
где
![]() в точке
в точке
![]() .
.
Все
методы спуска, в которых вектор
![]() совпадает
с антиградиентом, называются
градиентными методами. Они отличаются
друг от друга только выбором шага.
Наибольшее применение нашли метод
наискорейшего спуска и метод дробления
шага. В методе наискорейшего спуска
величина
определяется из условия
совпадает
с антиградиентом, называются
градиентными методами. Они отличаются
друг от друга только выбором шага.
Наибольшее применение нашли метод
наискорейшего спуска и метод дробления
шага. В методе наискорейшего спуска
величина
определяется из условия
 ,
,
т. е. на каждом шаге решается одномерная задача минимизации. Для решения этой задачи можно применить метод золотого сечения. Отметим, что на двух последовательных шагах решения направления спуска ортогональны. Для окончания процесса счета можно использовать различные критерии. Например, счет можно прекратить, если выполняется условие
grad
f(
(k+1))
<
, где
grad f
=
![]() .
В этом случае полагаем
.
В этом случае полагаем
![]() .
.
45.Метод покоординатного спуска.
Метод применяется для отыскания минимума функции n перемен- ных. Выбирается некоторое начальное приближение х(0) точки минимума функции. Затем выбирается направление спуска параллельно оси 0х1 и решается задача одномерной минимизации функции. Величина 0 определяется из условия
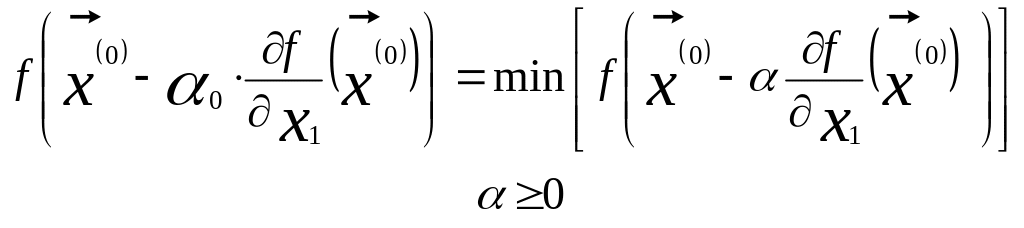
.
Затем
определяется первое приближение точки
минимума
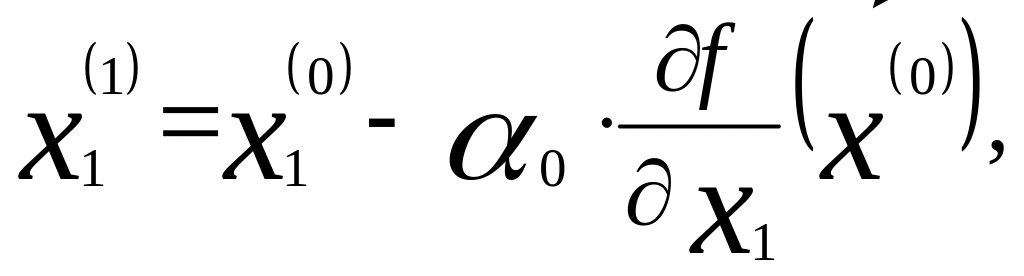 а все остальные координаты остаются
без измене- ния. При следующем уточнении
точки минимума спуск производится вдоль
линии, параллельной оси 0х2. Величина a1
определяется из условия
а все остальные координаты остаются
без измене- ния. При следующем уточнении
точки минимума спуск производится вдоль
линии, параллельной оси 0х2. Величина a1
определяется из условия
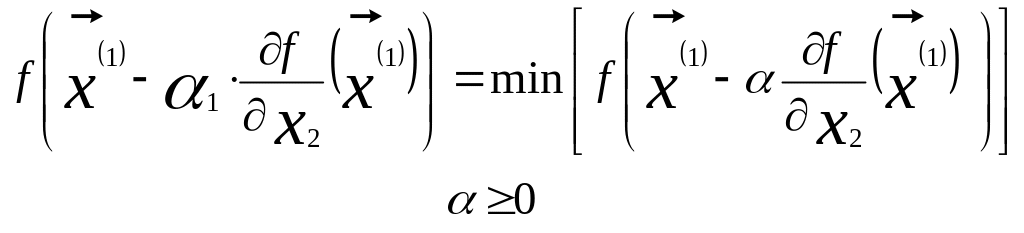 .
.
Затем
определяется второе приближение точки
минимума
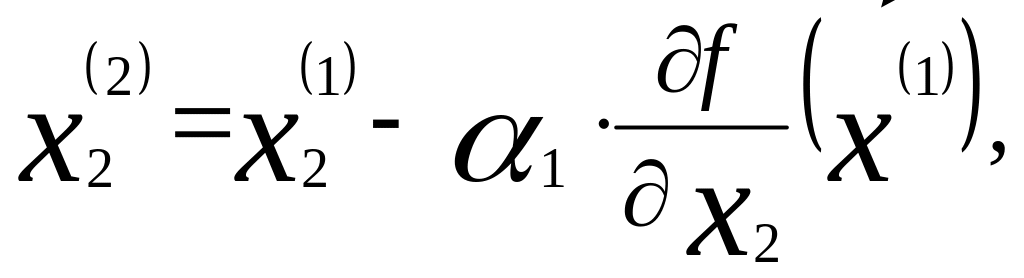 а все остальные координаты остаются
без изменения. Аналогичным способом
спуск продолжается в направлении
следующих координат. После этого спуск
снова начинается в направлении пер-
вой, второй и т.д. координаты. Процесс
заканчивается при выполнении условия
а все остальные координаты остаются
без изменения. Аналогичным способом
спуск продолжается в направлении
следующих координат. После этого спуск
снова начинается в направлении пер-
вой, второй и т.д. координаты. Процесс
заканчивается при выполнении условия
grad
f(![]() )
<
.
)
<
.
Пример. Найти минимум функции
f (x1,x2) = 2x1 - 3x2 + exp (x12 + x24).
Задачу
решим методом покоординатного спуска.
Возьмем
= 0,001. В качестве начального выберем
вектор![]() = (0;0). Тогда
= (0;0). Тогда
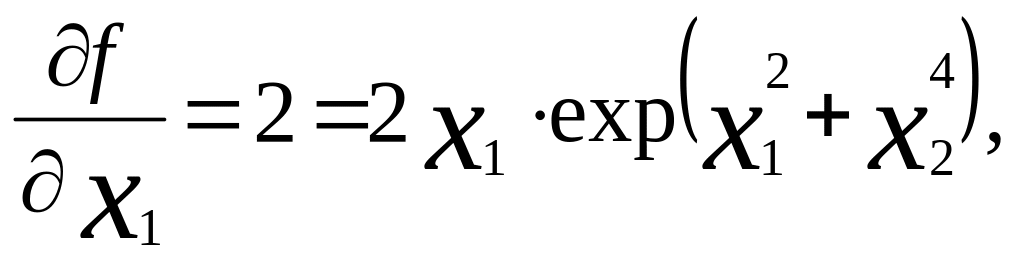
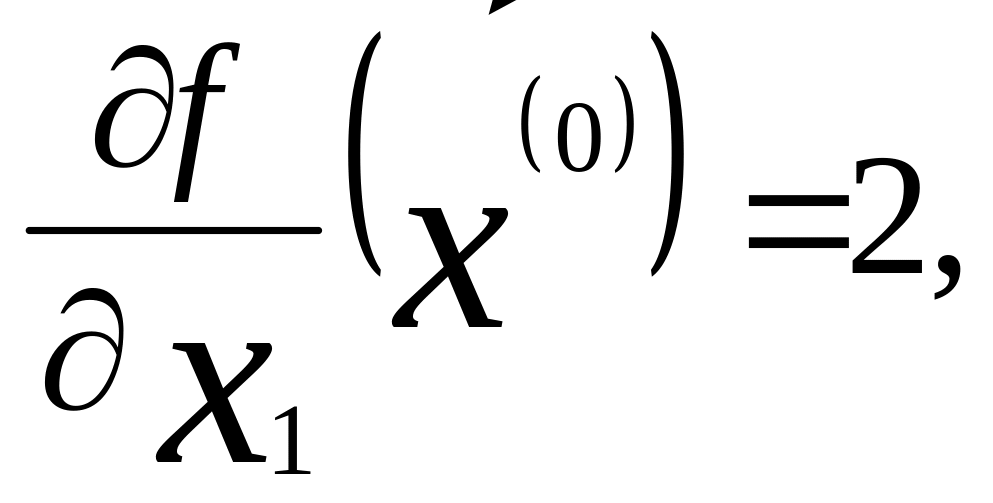
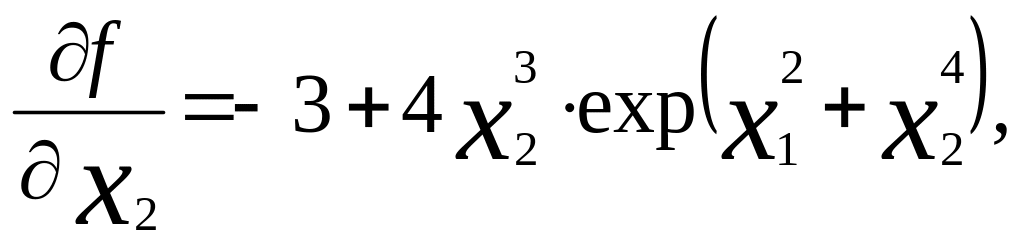
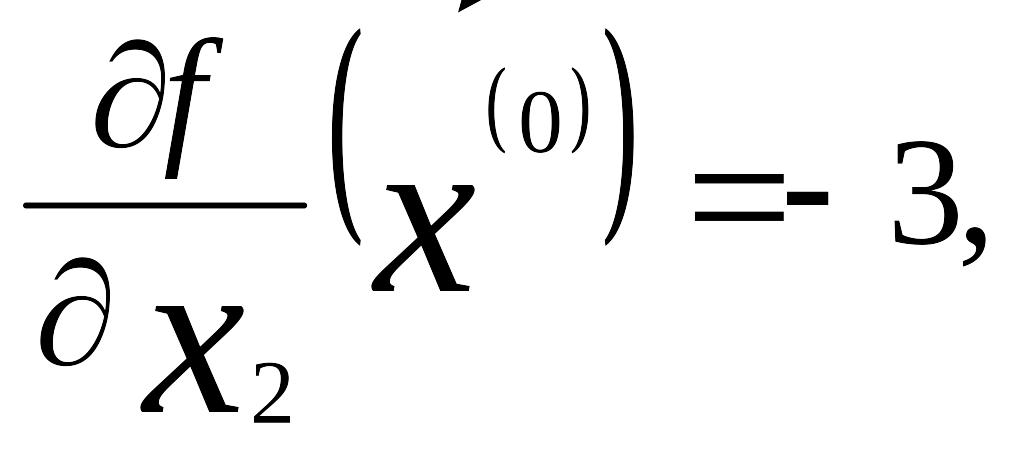
grad
f =
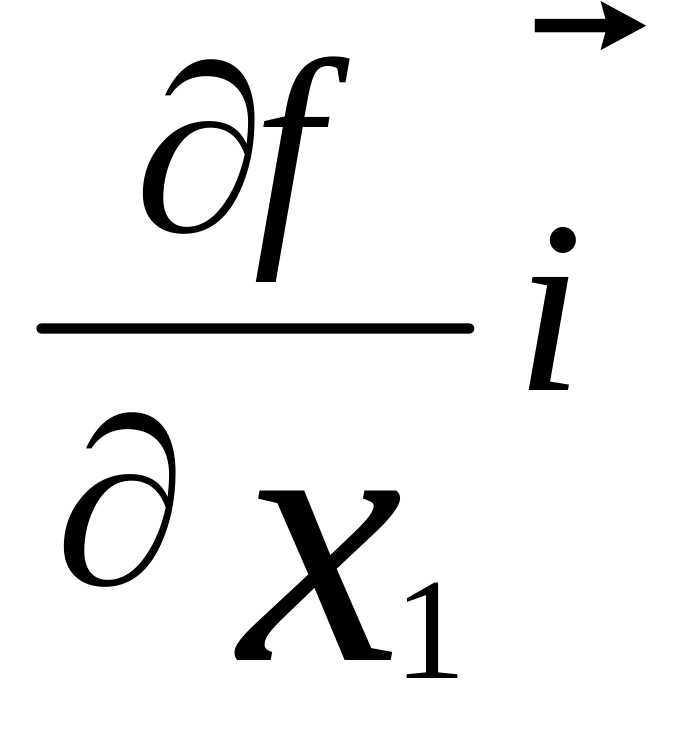 +
+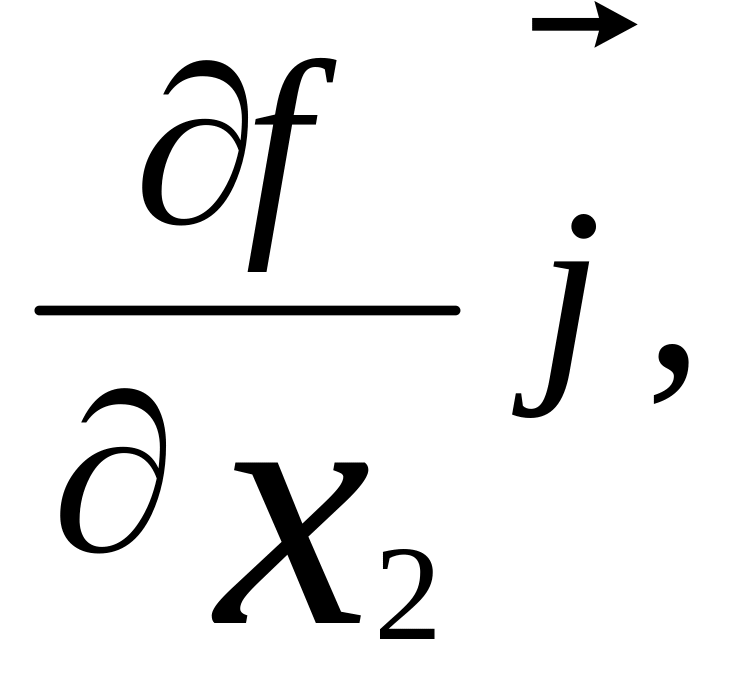 grad
grad
![]()
![]()
grad
![]()
3,60555.
3,60555.
Составим
функцию
 которую нужно минимизировать по параметру
a. Для минимизации этой функции применим
метод дробления шага.
которую нужно минимизировать по параметру
a. Для минимизации этой функции применим
метод дробления шага.
